清华大学运筹学课件(完整课件).ppt

清华大学运筹学课件(完整课件).ppt

《清华大学运筹学课件(完整课件).ppt》由会员分享，可在线阅读，更多相关《清华大学运筹学课件(完整课件).ppt（211页珍藏版）》请在冰豆网上搜索。

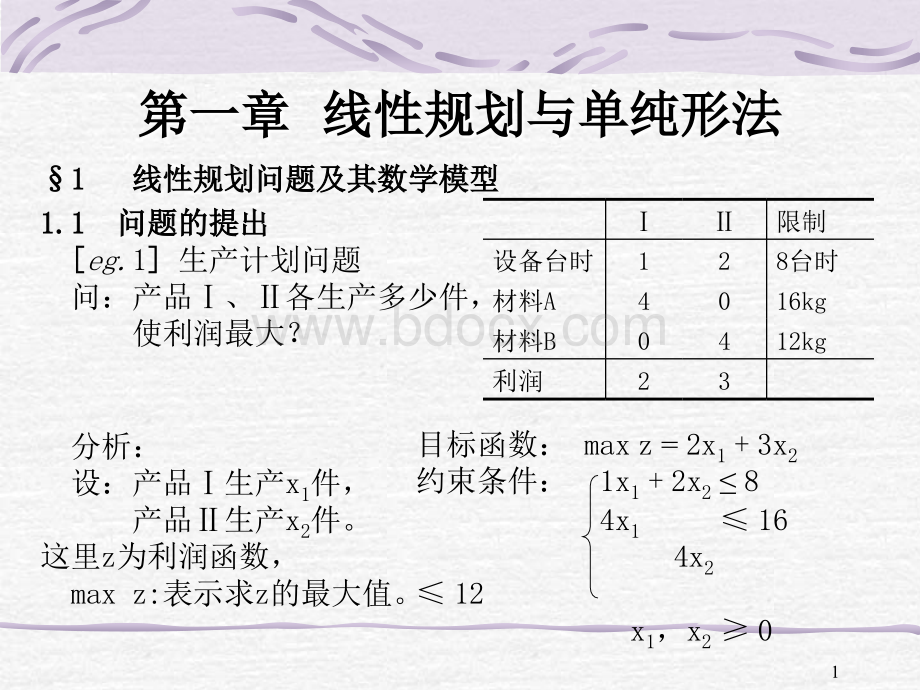
第一章第一章线性规划与单纯形法线性规划与单纯形法11线性规划问题及其数学模型线性规划问题及其数学模型1.11.1问题的提出问题的提出eg.1生产计划问题问：

产品、各生产多少件，使利润最大？

限制设备台时128台时材料A4016kg材料B0412kg利润23分析：

设：

产品生产x1件，产品生产x2件。

这里z为利润函数，maxz:

表示求z的最大值。

目标函数：

maxz=2x1+3x2约束条件：

1x1+2x284x1164x212x1，x201eg.2污水处理问题环保要求河水含污低于2，河水可自身净化20%。

问：

化工厂1、2每天各处理多少污水，使总费用最少？

分析：

化工厂1处理污水x1万m3,化工厂2处理污水x2万m3。

minz=1000x1+800x2（2-x1）/5002/1000（1-0.2）（2-x1）+1.4-x2/（500+200）2/1000x12x21.4x1，x20这里minz:

表示求z的最小值。

200万m3500万m32万m31.4万m3化工厂1化工厂21000元/万m3800元/万m32线性规划的数学模型：

线性规划的数学模型：

max（min）z=c1x1+c2x2+cnxna11x1+a12x2+a1nxn（=,）b1a21x1+a22x2+a2nxn（=,）b2am1x1+am2x2+amnxn（=,）bmx1，x2，xn03说明：

（1）决策变量：

x1，x2，xn。

一组决策变量表示为问题的一个方案；

（2）目标函数：

max（min）zz为决策变量的线性函数;（3）约束条件一组线性不等式。

cj为价值系数,bi为资源，aij为技术系数（i=1,m;j=1,n）.41.21.2图解法图解法eg.eg.33用图解法求用图解法求eg.eg.11。

maxmaxzz=2x2x11+3x3x221x1x11+2x2x22884x4x1116164x4x221212xx11，xx2200解：

（1）建立xx11-xx22坐标；x2x1

（2）约束条件的几何表示；Q1Q2Q3Q4（3）目标函数的几何表示；*zz=2x2x11+3x3x22o435首先取z=0，然后，使z逐渐增大，直至找到最优解所对应的点。

*可见，在Q2点z取到最大值。

因此，Q2点所对应的解为最优解。

Q2点坐标为（4，2）。

即:

x1=4，x2=2由此求得最优解：

xx11*=4x4x22*=22最大值：

maxmaxzz=zz*=2x2x11+3x3x22=14（14（元元）x2x1Q1Q2（4,2）Q3Q4*436讨论：

（1）唯一最优解maxmaxzz=zz*时，解唯一，如上例。

（2）无穷多最优解eg.4对eg.1，若目标函数zz=2x2x11+4x4x22，此时表示目标函数的直线与表示条件的直线平行，最优点在线段Q3Q2上。

即存在无穷多最优解。

x2x1Q1Q2（4,2）Q3（2,3）Q4o43*7（3）无界解eg.5maxz=2x1+3x24x116x1，x20则x2，z。

即存在无界解。

在实际问题中，可能是缺少约束条件。

o2248（4）无可行解eg.6maxz=2x1+3x22x1+4x28x1+x21x1，x20无公共部分，无可行域。

即无可行解。

在实际问题中，可能是关系错。

1124x1x291.31.3线性规划的标准型线性规划的标准型1、标准型maxz=c1x1+c2x2+cnxna11x1+a12x2+a1nxn=b1a21x1+a22x2+a2nxn=b2am1x1+am2x2+amnxn=bmx1，x2，xn010用向量表示11用矩阵描述为：

maxz=CXAX=bX0其中:

X=（x1,x2,xn）TC=（c1,c2,cn）b=（b1,b2,bm）T1222、标准型的化法标准型的化法

（1）

（1）minmaxminzminmaxminz=cxcx=-max（-z）-max（-z）max（-z）max（-z）=-minz-minz=-cxcx令令zz=-z-z则则maxzmaxz=-cxcx

（2）

（2）不等式不等式（，）对对于于“”情情况况：

在在“”“”左左边边加加上上一一个个松松弛弛变变量量（非非负负），变为等式；变为等式；对对于于“”“”情情况况：

在在“”“”左左边边减减去去一一个个剩剩余余变变量量（非非负负），变为等式。

，变为等式。

注意：

松弛变量、剩余变量在目标函数中的价值系数为注意：

松弛变量、剩余变量在目标函数中的价值系数为00。

（3）（3）无约束变量无约束变量令令xxkk=xxkk-xxkk”，xxkk,x,xkk”00，代入即可。

代入即可。

13eg.eg.77将下述问题化为标准型将下述问题化为标准型minzminz=-x-x11+2x+2x22-3x-3x33xx11+x+x22+x+x3377xx11-x-x22+x+x3322-3x-3x11+x+x22+2x+2x33=55xx11,x,x2200，xx33无约束无约束解：

令解：

令xx33=xx33-x-x33”，xx33,x,x33”00；式加上一个松弛变量式加上一个松弛变量xx44；式减去一个剩余变量式减去一个剩余变量xx55；令令zz=-z-zmaxzmaxz=xx11-2x2x22+3（x3（x33-xx33”）+0x0x44+0x0x55xx11+xx22+（x+（x33-xx33”）+xx44=77xx11-xx22+（x+（x33-xx33”）-xx55=22-3x-3x11+xx22+2（x2（x33-xx33”）=55xx11,x,x22,x,x33,x,x33”,x,x44,x,x5500141.41.4线性规划解的概念线性规划解的概念设线性规划为maxmaxzz=CXCXAXAX=bbXX00AA为为mmnn矩阵矩阵,nnm,Rankm,RankAA=m（Am（A为行满秩矩阵）为行满秩矩阵）11、可行解：

满足条件、可行解：

满足条件、的的XX；22、最、最优解：

解：

满足足条件条件的可行解；的可行解；33、基：

取、基：

取BB为AA中的中的mmmm子矩子矩阵，RankRankBB=mm，则称称BB为线性性规划划问题的一个基。

的一个基。

取取BB=（p（p11,p,p22,p,pmm）ppjj=（a（a1j1j,a,a2j2j,a,amjmj）TT则称则称xx11,x,x22,x,xmm为基变量，其它为非基变量。

为基变量，其它为非基变量。

1544、基解：

取、基解：

取BB=（p（p11,p,p22,p,pmm）aa1111,a,a1m1mxx11aa1m+11m+1,a,a1n1nxxm+1m+1bb11+=aam1m1,a,ammmmxxmmaamm+1mm+1,a,amnmnxxnnbbmm基基基变量基变量非基非基非基变量非基变量令令xxm+1m+1=xxnn=0（0（非基变量为非基变量为0）0）则则BXBXBB=bb165、基可行解满足式要求的基解。

如右图所示，各边交点O,QO,Q11,Q,Q22,Q,Q33,Q,Q44均为基可行解；而其延长线的交点Q5为基解，但不是基可行解。

O（0,0）O（0,0）QQ11（4,0）（4,0）QQ22（4,2）（4,2）QQ44（0,3）（0,3）QQ33（2,3）（2,3）QQ55（4,3）（4,3）6、可行基基可行解对应的B为可行基。

可行解可行解基可行解基可行解非可行解非可行解基解基解1722线性规划问题的几何意义线性规划问题的几何意义2.12.1基本概念基本概念11、凸集：

设、凸集：

设KK为为EEnn（n（n维欧式空间维欧式空间）的一点集，的一点集，XX

（1）

（1）KK，XX

（2）

（2）KK。

若若XX

（1）

（1）+（1-）X+（1-）X

（2）

（2）KK，则称则称KK为凸集。

（为凸集。

（0011）非凸集XX

（1）

（1）XX

（1）

（1）XX

（2）

（2）XX

（2）

（2）凸集XX

（1）

（1）XX

（2）

（2）XX

（2）

（2）XX

（1）

（1）1822、顶点：

、顶点：

XXKK，XX

（1）

（1）KK，XX

（2）

（2）K（K（任意两点任意两点）。

若。

若XX不能用不能用XX

（1）

（1）+（1-）X+（1-）X

（2）

（2）表示，则称表示，则称XX为为KK的一个顶点。

的一个顶点。

（0（01）1）注：

顶点所对应的解是基可行解。

注：

顶点所对应的解是基可行解。

33、凸组合：

设、凸组合：

设XX（i）（i）EEnn，若存在若存在00ii11，ii=1,2,1,2,k,k，使使,则称则称XX为为XX（i）（i）（i=1,2,（i=1,2,k）,k）的凸组合。

的凸组合。

2.22.2基本定理基本定理11、定理、定理11若线性规划存在可行域，则若线性规划存在可行域，则:

可行域可行域DD=X|AXX|AX=b,Xb,X00为凸集。

为凸集。

19证明：

证明：

设设XX

（1）

（1）=（=（x11

（1）

（1）,x22

（1）

（1）,xnn

（1）

（1）TTDD；XX

（2）

（2）=（=（x1

（2）

（2）,x22

（2）

（2）,xnn

（2）

（2）TTDD；（X（X

（1）

（1）XX

（2）

（2）有有AXAX

（1）

（1）=bb，AXAX

（2）

（2）=bb令令XX=XX

（1）

（1）+（1（1-）X）X

（2）

（2）（0（0010100XX00，即即DD为凸集为凸集2、定理2线性规划的基可行解对应于可行域的顶点。

3、定理3若线性规划有解，则一定存在基可行解为最优解。

2033单纯形法单纯形法基本思路：

基本思路：

从可行域的一个顶点到另一个顶点迭代求最优解。

3.13.1初始基可行解的确定初始基可行解的确定1、松弛基（松弛变量对应的B）eg.8maxz=x1+3x2x1+2x232x1+3x24x1,x20maxz=x1+3x2+0x3+0x4x1+2x2+x3=32x1+3x2+x4=4x1,x2,x3,x40化标准型取x3、x4为基变量,令非基变量x1=x2=0初始基可行解：

X（0）=（0034）T212、观察法eg.9maxz=x1+3x2+2x3+x4x1+2x2+3x3=33x2+x3+x4=4x1,x2,x3,x40选XB=（x1x4）T令x2=x3=0则初始基可行解：

X（0）=（3004）T223、人工基eg.10maxz=x1+2x2+3x3x1+3x2+2x3=32x1+x2+x3=4x1,x2,x30分析：

A=132211找不到单位矩阵基引入人工变量为初始基变量（2个）233.23.2最优性的检验与解的判别最优性的检验与解的判别24则25解的判别：

1.若，则此时的基可行解为最优解；2.若存在某个非基变量的检验数，且，则该线性规划问题具有无界解（或称无最优解）；3.若所有，又，对于某个非基变量有，则该线性规划问题具有无穷多最优解。

263.33.3基变换基变换273.43.4旋转运算（消元运算）旋