医学统计学知识梳理.docx
《医学统计学知识梳理.docx》由会员分享,可在线阅读,更多相关《医学统计学知识梳理.docx(20页珍藏版)》请在冰豆网上搜索。
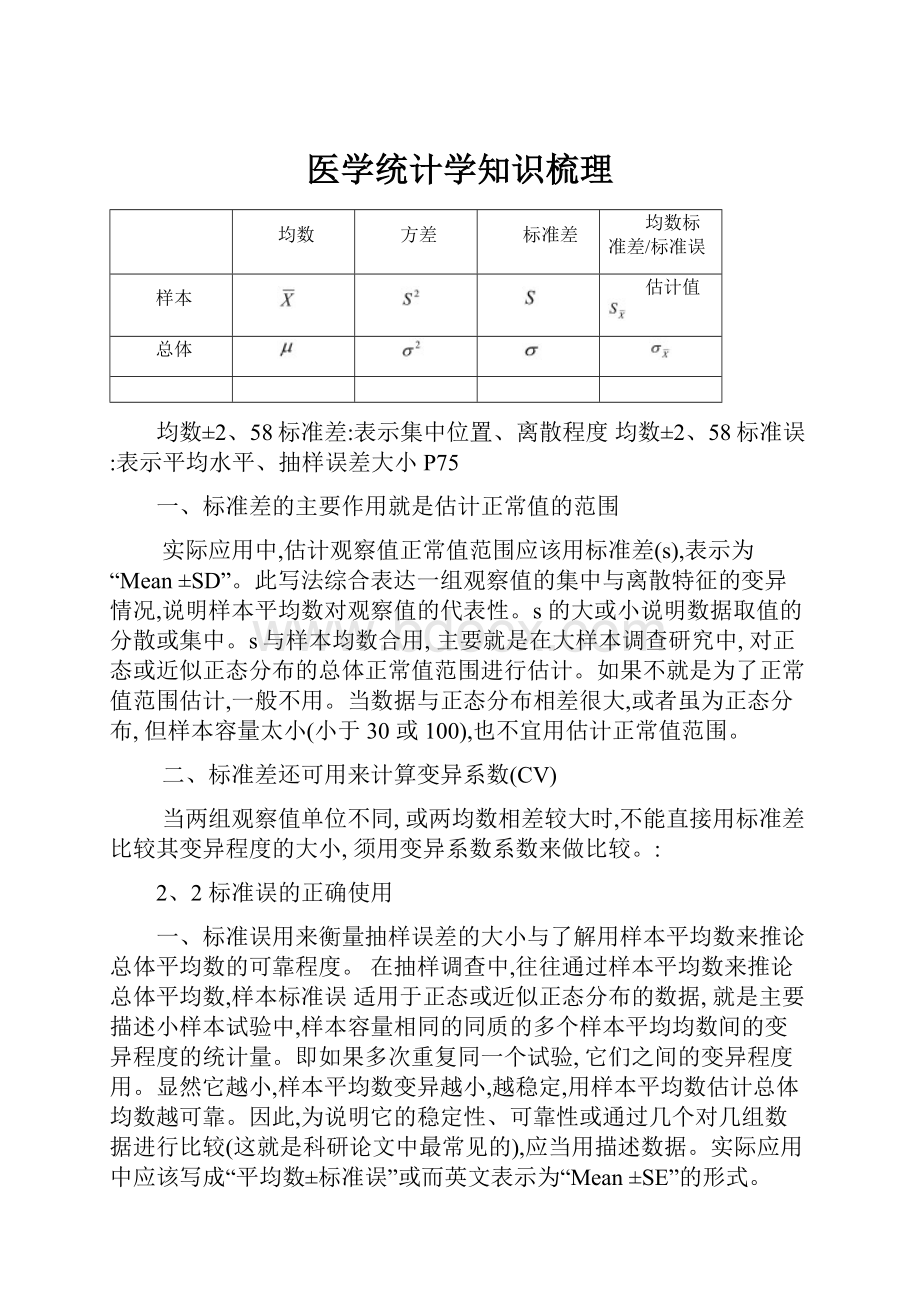
医学统计学知识梳理
均数
方差
标准差
均数标准差/标准误
样本
估计值
总体
均数±2、58标准差:
表示集中位置、离散程度均数±2、58标准误:
表示平均水平、抽样误差大小P75
一、标准差的主要作用就是估计正常值的范围
实际应用中,估计观察值正常值范围应该用标准差(s),表示为“Mean ±SD”。
此写法综合表达一组观察值的集中与离散特征的变异情况,说明样本平均数对观察值的代表性。
s 的大或小说明数据取值的分散或集中。
s与样本均数合用, 主要就是在大样本调查研究中, 对正态或近似正态分布的总体正常值范围进行估计。
如果不就是为了正常值范围估计,一般不用。
当数据与正态分布相差很大,或者虽为正态分布, 但样本容量太小(小于30 或100),也不宜用估计正常值范围。
二、标准差还可用来计算变异系数(CV)
当两组观察值单位不同, 或两均数相差较大时,不能直接用标准差比较其变异程度的大小, 须用变异系数系数来做比较。
:
2、2 标准误的正确使用
一、标准误用来衡量抽样误差的大小与了解用样本平均数来推论总体平均数的可靠程度。
在抽样调查中,往往通过样本平均数来推论总体平均数,样本标准误 适用于正态或近似正态分布的数据, 就是主要描述小样本试验中,样本容量相同的同质的多个样本平均均数间的变异程度的统计量。
即如果多次重复同一个试验, 它们之间的变异程度用。
显然它越小,样本平均数变异越小,越稳定,用样本平均数估计总体均数越可靠。
因此,为说明它的稳定性、可靠性或通过几个对几组数据进行比较(这就是科研论文中最常见的),应当用描述数据。
实际应用中应该写成“平均数±标准误”或而英文表示为“Mean ±SE”的形式。
二、标准误还可以进行总体平均数的区间估计与点估计(置信区间)。
根据正态分布原理, 与 合用还可以给出正态总体平均数的可信区间估计即推论总体平均数的可靠区间,例如常用 (其中t0、05 (n-1) 为样本容量就是n的t界值)表示总体均值的95%可信区间, 意指总体平均数有95%的把握在所给范围内。
三、标准误还可用来进行平均数间的显著性检验,从而判断平均数间的差别就是否就是由抽样误差引起的。
例如:
某当地小麦良种的千粒重=34克,现在从外地引入一新品种,通过多小区的田间试验得到千粒重的平均数=35、2克,问新引进品种千粒重与当地良种有无显著差异?
新引进品种千粒重与当地良种有无显著差异实质就是判断与的差别就是否就是有田间试验就是抽样误差引起,所以要进行显著性检验,这里用t测验进行检验,而,由于,故,所以认为新引进品种千粒重与当地良种千粒重的不同就是由于田间试验就是抽样
误差引起,因此她们之间无显著差异。
所以在进行平均数间的显著性检验就是必须用到。
总之,标准差与标准误最常用的统计量,二者都就是衡量样本变量(观察值) 随机性的指标,只就是从不同角度来反映误差,二者在统计推断与误差分析中都有重要的应用。
如果没有标准差,人们就无法瞧出一组观察值间变异程度有多大,这些数字到底有无代表性,如果没有标准误又很难瞧出我们的样本平均数就是否可以代表总体平均数。
所以二者都非常重要。
定量资料的统计描述:
频数分布表:
全距,R=最大值-最小值;组距=全距/组数,(组数8-9人一组)
频数分布图:
直方图
集中位置的描述:
平均数3
1、算数均数:
μ总体均数,
样本均数。
适用定量资料,对称分布,正态或近似正态
2、几何均数:
G,适用变量值呈倍数关系,偏态尤其对数变换后正态或近似正态
3、中位数:
M,各种分布(不对称,两端无确切值,分布不明确),正态等于算数均数,对数正态等于几何均数。
离散程度描述:
5
1.极差:
R,同全距,各种分布,但一般单峰、对称、小样本
2.四分位数间距:
P75—P25,(不对称,两端无确切值,分布不明确),P25,P50,P75,共三点将全部观察值分为四部分
3.方差:
总体σ2,样本S2(计算时除以自由度n-1)。
单峰对称。
4.标准差:
总体σ,样本S。
单峰对称,对数变换后正态或近似正态使用几何标准差。
5.变异系数:
CV=S/
*100%。
适用不同计量单位(身高与体重),或均数相差很大
正态分布及其应用:
N(μ,σ2)
特征:
4①横轴上方均数处最高;②均数为中线,左右对称;③位置参数/总体均数μ,形态参数/标准差σ;④曲线下面积分布有一定规律,对称,1、645—90、00%,1、96—95、00%,2、58—99、00%。
6.正态分布:
N(
)经标准化转换
为标准正态分布/Z分布:
Z(0,1)
7.制定医学参考限值时,分双侧(±)、单侧,单侧又分只有下限(-)、只有上限(+)。
定性资料描述:
分类/计数资料,性别,疾病感染情况,病情轻重、、、,相对数进行统计描述。
相对数:
3
1.率:
频率(发病率、患病率),0到1之间;速率(肿瘤患者5年生存率),分母乘以时间数(125人追踪2年死亡2人,年死亡率=2/125*2*100%)0到∞。
2.构成比:
3.相对比:
两个有关联的指标比值(变异系数,相对危险度,比值比、、)
应用注意:
①足够的观察单位数;
②不能以构成比代替率,事物内部各组分所占比重不能说明某现象发生的频率或强度大小;
③分别将分子与分母合计求合计率;
④相对数的比较注意可比性,其她的年龄、性别等相同或相近,可分层或标准化再比较;
⑤样本率、样本构成比应做假设检验再比较(就是比较其所代表的总体~有无差异)。
率的标准化:
标准化率:
p’=
(pi被标化组死亡率,Ni标准组年龄别人口,N标准组总人口)
标准化死亡率比:
SMR=被标化组实际死亡数/预期死亡数
被标化组实际死亡数=本年龄组死亡率*标准组本年龄组人口(用被标化组年龄别死亡率去预测标准人口中可能死亡人数)
总体均数的估计:
抽样误差:
由个体变异产生的、随机抽样引起的样本统计量与总体参数间的差异。
样本均数的标准差=均数的标准误,其估计值:
(进行一次抽样即可估计均数标准误)
t分布
(总体均数的区间估计,t检验、、、)
t分布特征:
①以t=0为左右对称的单峰分布;
②曲线形态取决于自由度大小,n越小,
越大,样本
间差异越大,n→∞,t分布就就是标准正态分布(Z分布)。
总体均数的估计:
点估计用
作为μ,无法评价可信程度。
区间估计:
2
1、单样本:
n不论大小,μ双侧(1-α)置信区间
(确切法)
n>100,t接近Z,μ双侧(1-α)置信区间
(1、6451、962、58)(正态近似法)
2、两样本:
两均数之差的标准误:
①n1、n2不论大小,
(确切法)
②n1、n2均较大时,t接近Z,则
(正态近似法)
两总体均数差值的置信区间:
(μ1-μ2)为
(t与Z根据条件可互换)
t检验:
Student’st检验,从样本均数推总体均数
条件:
①t检验,单样本中,n<50,总体正态分布。
②t’检验,两小样本,总体正态分布,但两样本总体方差不等。
公式好复杂,P96
③Z检验,两大样本,n均>50,单峰、近似正态。
1、单样本t检验:
样本所代表的总体均数μ与已知总体均数μ0比较
2、配对t检验:
①配对的两受试对象分别接受2种不同处理;②同一样品用两种方法或仪器检测;③同一受试对象两不同部位测定数据。
H0为两总体均数相同,差值的样本均数
所代表的总体均数
为0,则
(n为对子数)
3、两独立样本/成组t检验:
两样本分别正态分布,H0为两总体均数相等,则
①n1、n2不论大小,
(确切法)
②n1、n2均>50,t接近Z,
(正态近似法)
4、两样本几何均数t检验:
(抗体滴度等)不服从正态,但服从对数正态,公式同成组t检验。
正态性检验:
①图示法:
P-P图法,Q-Q图法
②统计检验法:
W检验(n≤50),矩法检验(总体偏度、峰度),D检验
方差齐性检验:
①两总体方差齐性检验,判断两总体方差就是否相等,F检验
(进行假设检验,α=0、10,查F界值表)
②多样本方差齐性检验:
q检验!
!
!
Levene检验(可两总体),Bartlett检验。
用于方差分析。
方差分析ANOVA/F检验:
总体均数之间差别?
多样本均数的比较,通过对数据变异的分析来推断两个/多个样本均数所代表的总体均数就是否有差别。
应用条件:
①各样本就是相互独立的随机样本,均服从正态;②各样本总体方差相等,即方差齐性。
总变异:
数据的均方MS总,处理影响+随机误差(个体差异+测量误差)
组间变异:
MS组间,处理因素的影响
组内变异:
MS组内,随机误差的影响
)
1、完全随机设计资料:
成组设计的多个样本~,单因素两水平/多水平方差分析。
3变异
同质的受试对象随机分配到各处理组,各组样本含量相等或不等。
SS总=SS组间+SS组内
V总=V组间+V组内
v总=N-1V组间=k-1V组内=N-k
)v1组间,v2组内
注意:
总体均数不全相同,两两之间比较用另外的方法。
2、随机区组设计资料;配伍组设计,两因素。
3变异
受试对象按照性质分成b个区组/配伍组,每个区组随机分配到k个处理组。
MS总=MS处理组+MS区组+MS误差
v总=v处理组+v区组+v误差=(处理-1)+(区组-1)+误差=N-1
同理:
总体均数不全相同,两两之间比较用另外的方法。
3、多个样本均数两两比较,即上面的“注意”、“同理”
①SNK法,q检验②Dunnett-t检验
4、交叉设计资料,分两阶段与多阶段(×)
两阶段交叉设计:
一、二组患者与A、B处理方法,一患者服药顺序A→B,二组患者B→A。
5、析因设计资料
6、重复测量资料
检验:
样本率或构成比推总体率/构成比之间两个及以上的比较
1、独立样本列联表资料
1)2×2列联表(四格表)成组连续性校正(Yates校正)3种
①
②(n≥40,1≤T<5)
③(n<40,或T<1)
(确切概率法,以上均适用)A实际频数,T理论频数(总有效率乘以各组人数)
2)R行×C列列联表资料多个样本率/两个或多个构成比
v=(R-1)(C-1)
注意:
①必须绝对数,不能相对数,因x2与频数有关;
②理论频数太小:
1/5以上格子的理论频数<5,或一个格子理论频数<1。
或计算最小理论频数
≥5,可以计算;(太小解决方法:
增大样本含量;确切概率法;与邻近行或列合并;删去)。
③有序多分类变量用秩与检验/Ridit检验;
④多个样本率(或构成比)拒绝无效假设时,只能说各总体率之间总的来说有差别,不能说明彼此之间有差别或两者之间有差别。
2、配对设计资料
1)配对2×2列联表配对设计且结果为“二分类”(独立列联表数据相互独立,配对设计为研究对象先按某种方式配对,再按两种属性统计,结果不就是相互独立)。
又称McNemar检验,H0成立:
B=C
连续性校正:
①
②b+c≤40,
2)配对R×R列联表求统计量T服从x2分布,自由度R-1
3、拟合优度的~
4、先行趋势的~
5、四格表的Fisher确切概率法,好复杂P147
秩与检验:
基于原始数据在整个样本中按大小排列所占的位次计算统计量,总体分布不明,少量离群值小样本。
1、符号秩与检验(Wilcoxon)单一样本与总体中位数的比较,配对设计计量差值的比较。
1)配对设计两样本~差值就是否来自于中位数为0的总体,进而推断两总体中位数有无差别
顺序:
求差值→编秩→分别求正、负秩与→确定检验统计量T→查T界值表
①编秩按绝对值由小到大;差值“0”舍去不计,n也减1;差值绝对值等,求平均秩次,正负相同可顺次编秩;
②正、负秩与T++T-=n(n+1)/2,相等则秩与计算无误。
③任取T+或T-作为统计量。
④5<n≤50,界值内P>α,界值外P<α,n大T大P减小。
概率内大外小相持较多,须校正
⑤N>50,近似正态分布,Z检验,公式P152
2)单一样本与总体中位数~差值=健康人群指标—样本数值公式同上
2、成组设计两样本的~两独立样本代表的总体分布位置就是否有差别
1)原始数据的两样本~两种处理方式的测量值统一从小到大排序
例数较小者为n1、T1,T1+T2=N(N+1)/2
n1≤10且n2-n1≤10时,查T界值表n1≠n2时T=T1,n1=n2时,T=T1或T2
n1>10或n2-n1>10时,计算Z值,查t界值表
2)等级资料的两样本~两种处理方法疗效的等级,
秩次范围:
两组数据按等级顺序(疗效)统一从小到大排序(如痊愈的两种处理结果合计数,1~合计数;痊愈合计数+1~显效合计数,类推)。
平均秩次:
痊愈组=1+痊愈合计数/2,显效组=痊愈合计数+1+显效合计数/2,类推。
秩与:
此处理组的此疗效原始数据×此疗效平均秩次。
例数较小者为n1、T1,
n1≤10且n2-n1≤10时,查T界值表n1≠n2时T=T1,n1=n2时,T=T1或T2
n1>10或n2-n1>10时,计算Z值,查t界值表
3、成组设计多样本~K-WH秩与检验
1)原始数据多样本~三种(、、、)处理方式数据统一从小到大编秩。
相同数据求平均秩次求各组秩与R1R2R3、、、、统计量H值
N=n1+n2+、、、
①组数k=3,ni≤5时,查H界值表;
②当k、ni超出H界值表,则使用v=k-1,x2≈H查x2界值表
2)等级资料多样本~编秩、各疗效组平均秩次、秩与同两样本等级资料
①组数k=3,ni≤5时,查H界值表;
②当k、ni超出H界值表,则使用v=k-1,x2≈H查x2界值表
3)多个独立样本间的多重比较K-WH秩与检验H1仅得到各总体分布位置不全相同,两两比较回答哪两个总体位置不同
H0:
任意两个处理组总体分布位置相同
H1:
任意两个处理组总体分布位置不同
4、随机区组设计的~配伍组
1)多个相关样本比较的FriedmanM检验多区组、多剂量(处理)
Ri为各处理组秩与,b为区组数,k处理组数
2)多个相关样本的两两比较
双变量关联性分析两随机变量的关联方向、密切程度
1、直线相关/简单相关两随机变量之间呈直线趋势的关系
1)直线相关系数/Pearson积矩相关系数
Lyy:
离均差乘积与
①r无单位,[-1,1];
②正、负号标示相关方向(正相关、负相关、零相关、散点为无相关);
③绝对值大小表示相关密切程度。
2)相关系数的统计推断对总体相关系数
就是否为0做假设检验
假设变量x、y均服从正态,H0:
=0,无直线相关关系H1:
≠0,有直线相关关系
t检验
自由度v=n-2
注意:
①相关分析前先绘制散点图;
②要求变量x、y均服从正态;
③出现离群点慎用相关(核实数据、重复观察);
④相关关系不一定就是因果关系;
⑤分层资料不可盲目合并。
2、秩相关不服从正态,总体分布未知,存在极端值,原始数据用等级表示
1)变量x、y分别从小到达编秩,p为x的秩次,q为y的秩次
Spearman秩相关系数/等级相关系数
同样[-1,1],正相关、负相关
2)假设检验
①n≤50,直接查等级相关系数界值表;
②n>50,公式同直线相关,做t检验。
3、分类变量的关联性统计量服从四格表x2分布,自由度为1,有关联,求Pearson列联系数
4、R×C列联表的关联性x2确切概率公式,自由度为(R-1)(C-1),有关联,求Pearson列联系数
直线回归分析一个变量预测另一个变量
1、直线回归方程的建立
1)
随x变化的方程为直线回归方程/直线回归模型
a为直线截距,x为0时y的平均估计值;
b为直线斜率/回归系数,x每改变一个单位时y的平均改变量;
个体观察值不一定总等于其均数,散点图各点不会恰好都在回归直线上。
2)方程的估计b=lxy/lxx
2、统计推断
1)总体回归系数β=0则无直线回归关系方差分析(F统计量)
SS总:
总离均差平方与,不考虑回归关系时y的总变异;
SS回:
回归平方与,y的总变异中回归关系所解释的部分,越大回归效果越好;
SS残:
残差平方与,除回归关系外所有因素对y的变异作用。
SS总=SS回+SS残v总=v回+v残v总=n-1v回=1v残=n-2
对应上式
有无直线关系①F检验
②t检验
2)总体回归系数β置信区间
3)决定系数R2
取值[0,1],表示回归贡献的相对程度。
生存分析不仅关心结局,还关心发生这种结局所经历的时间
1、特点:
①蕴含结局、时间两个信息;
②结局为两分类互斥事件;
③一般通过随访收集,从某一时间点开始(确诊、入院、实施手术、、、),到某规定时间点截止;
④常因失访造成研究对象生存时间数据不完整,分布类型复杂,通常不服从正态。
2、基本概念
①死亡事件:
失效事件/终点事件。
②生存时间:
观察到的存活事件。
完全数据:
观察起点到死亡事件的时间。
截尾数据:
结尾值/删失值/终检值,除死亡事件的其她原因引起的截止(失访、退出、观察终止(“+”表示))。
此时使用校正人口数=年初观察例数—1/2截尾例数。
③死亡概率:
单位时段开始存活的个体在该时段内死亡的可能性
=d/n
生存概率:
单位时段开始存活的个体到时段结束时仍存活的可能性
(有截尾,分母校正。
)
④生存率:
观察对象活过tk时刻的概率,
(T为观察对象存活时间,有截尾,分母校正)。
实为累积生存概率,3年生存率=第一年、第二年、第三年生存概率的连乘积。
⑤生存曲线:
各时点生存率连接(阶梯形,标有截尾值)。
⑥中位生存时间:
半数生存期,生存率为0、5时对应的生存时间,表示50%的观察对象可以活到此时。
3、未分组资料的~
每个观察单位的原始测得值组成的资料。
乘积极限法/Kaplan-Meier法/K-M法
注意:
统计时间比tk时间少1,如生存时间t为4月的生存率为p1*p2*p2,t为5月的生存概率为1-d4/n4
估计总体生存率的置信区间
SE为S的标准误
4、分组资料的~将原始资料按照生存时间分组,再进行分析。
寿命表法
5、生存曲线的比较对数秩检验
假定无效假设成立,两总体生存曲线位置相同,理论死亡数与实际死亡数相差应该不大
①乘积极限法估计各组患者不同时点的生存率,绘制生存曲线;
②将两组患者按生存时间统一从小到大排序,并标明组别
统计量计算
假设检验:
检验水准α,可能性P值,无效假设,备择假设。
Ⅰ型错误:
=α,弃真,假阳性,误诊。
拒绝实际正确的H0。
样本量确定时,α、β呈反比。
Ⅱ型错误:
=β,存伪,假阴性,漏诊。
不拒绝实际错误的H0。
检验效能:
=(1-β),检验方法能发现H1成立的能力。
【Ⅰ型错误、Ⅱ型错误】
1、重点减少Ⅰ型错误:
α可取小,如0、01;重点减少Ⅱ型错误:
α可取大,如0、2。
2、α越大,Ⅱ型错误越小,检验效能1-β越大。
3、P≤α拒绝H0时,只犯Ⅰ型错误;P>α不拒绝H0时,只犯Ⅱ型错误。
4、双侧检验P≤α,单侧必得P≤α;单侧检验P>α,双侧必得P>α。
5、单侧检验易犯Ⅰ型错误,双侧检验易犯Ⅱ型错误,单侧效能高于双侧。
【t检验】
含义
一种以t分布为基础,以t值为检验统计量的计量资料的假设检验方法。
基本思想
假设在H0成立的条件下做随机抽样,按照t分布的规律获得现有样本检验统计量t值的概率为P,将P值与事先设定检验水准α进行比较,判断就是否拒绝H0
应用条件
①独立性;②正态性(可用正态性检验来确认);③方差齐性(可由方差齐性检验来认定)。
主要用途
①单个样本均数与总体均数的比较;
②配对设计资料的差值均数与总体均数的比较;
③成组设计的两样本均数差异的比较。
【方差分析】
含义
一种以数据分析的变异为基础,以F值为统计量的计量资料的假设检验方法。
基本思想
将全部观察值之间的总变异按设计类型分解为两个或多个组成部分,通过比较不同变异来源的均方,借助F分布做出统计推断。
应用条件
①独立性;②正态性(可用正态性检验来确认);③方差齐性(可由方差齐性检验来认定)。
主要用途
多个样本均数的比较(三个及三个以上)
【x2检验】
含义
一种以x2分布为基础,以x2值为检验统计量的计数资料的假设检验方法。
基本思想
通过x2值的大小反映实际频数(A)与理论频数(T)的符合程度,在H0成立时,实际频数(A)与理论频数(T)的相差不应该很大,果实际频数(A)与理论频数(T)的相差很大,则H0成立的可能性很小。
应用条件
①独立性;②正态性(可用正态性检验来确认);③方差齐性(可由方差齐性检验来认定)。
主要用途
①推断两个或两个以上总体率(或构成比)之间有无差别;
②两变量间有无相互关系;③检验频数分布的拟合优度。
2×2表的x2检验的注意事项
①当n≥40且所有T≥5时,用2×2表x2检验的基本公式或专用公式计算x2值;
②当n≥40但有1≤T<5时,需要用校正公式计算x2值;
③当n<40或有T<1时,不宜计算x2值,需采用Fisher确切概率法直接计算概率。
R×C表的x2检验的注意事项
①允许有不超过1/5的基本格子理论频数大于1小于5,但不能有理论频数小于1;
②如果有1/5以上格子的理论频数大于1小于5,或有1个格子的理论频数小于1,可增加样本含量。
【非参数检验的优、缺点】
优点:
①适用于任何分布的资料;
②不受总体方差一致的限制;
③可用于等级资料的统计分析;
④有些问题本身没有适当的参数检验方法而非参数检验则恰能处理。
缺点:
①由于它没有充分利用原始数据中所提供的信息故检验效能低;
②其效果有一定近似性。
【直线回归与直线相关分析区别与联系】
VS
直线相关
直线回归
区别
资料要求不同
两个变量就是双变量正态分布,两者无主次之分。
要求应变量y服从正态分布,自变量x就是能精确测量或控制的变量。
统计意义不同
反映两变量间的相互关系,关系时互相平等的。
两变量之间的数量依存关系,表明y如何依赖x而变化。
分析目的不同
具有直线关系的两变量间关系的方向、密切程度。
回归系数b表示x每改变一个单位所引起的y的平均改变量。
计算公式
b=lxy/lxx
取值范围
[-1,1]
(-∞,∞)
单位
无
如身高、体重的单位
联系
对同一双变量正态资料,关系的方向一致:
其r与b的正负号一致。
假设检验等价:
对同一样本,
双变量正态分布,r与b可相互换算,
但就是r大小与b的大小无关?
?
?
!
!
!
!
!
回归可以解释相关:
回归分析中的决定系数在数值上等于相关系数的平方,即
。
【秩与检验】
含义
亦称符号秩与检验或Wilcoxon配对法,属于非参数检验(不依赖于总体分布类型,不对总体参数进行推断,只就是通过样本观察值推断总体的分布或分布位置就是否有差别)。
基本思想
在H0成立的前提下,差