分析正弦交流电路的相量法.docx
《分析正弦交流电路的相量法.docx》由会员分享,可在线阅读,更多相关《分析正弦交流电路的相量法.docx(14页珍藏版)》请在冰豆网上搜索。
分析正弦交流电路的相量法
2.1.3正弦交流电路的功率、相量法
一、正弦交流电路的功率
(一)、瞬时功率
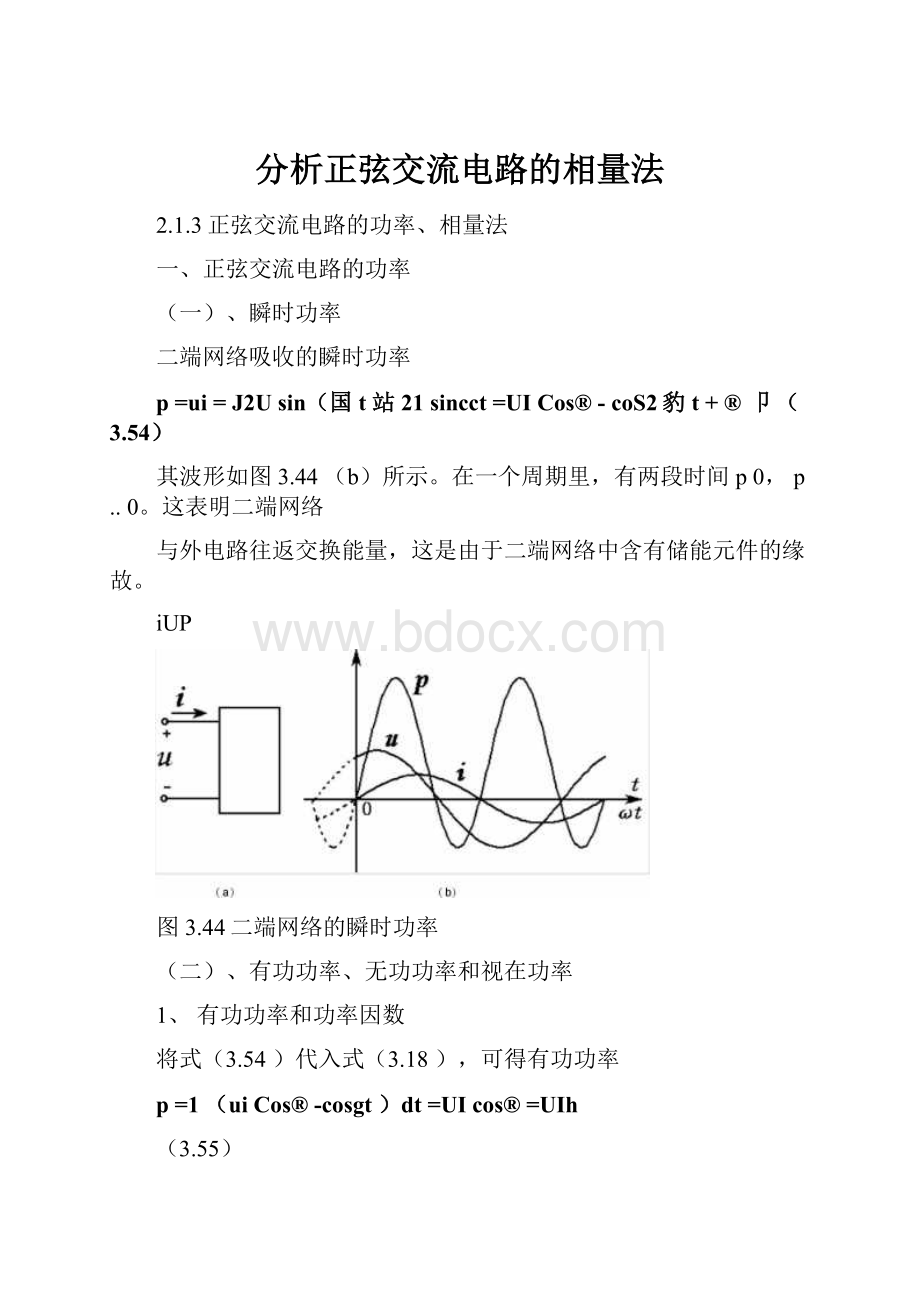
二端网络吸收的瞬时功率
p=ui=J2Usin(国t站21sincct=UICos®-coS2豹t+®卩(3.54)
其波形如图3.44(b)所示。
在一个周期里,有两段时间p0,p..0。
这表明二端网络
与外电路往返交换能量,这是由于二端网络中含有储能元件的缘故。
iUP
图3.44二端网络的瞬时功率
(二)、有功功率、无功功率和视在功率
1、有功功率和功率因数
将式(3.54)代入式(3.18),可得有功功率
p=1(uiCos®-cosgt)dt=UIcos®=UIh
(3.55)
式中’=COS:
:
称为二端网络的功率因数。
由于能量守恒,所以二端网络吸收的有功功率等于各部分吸收的有功功率的和。
2、无功功率
无功功率定义为
Q=Ulsin®(3.56)
对于电感性二端网络,:
:
・0,Q•0,二端网络接受无功功率;对于电容性二端网络,
--0,Q0,二端网络发出无功功率。
在既有电感又有电容的二端网络中,其无功功率
应等于两者的代数和,即
Q=QLQC
一般来说,二端网络吸收的无功功率等于各部分吸收的无功功率的代数和。
3、视在功率
视在功率定义为
S=UI(3.57)
其SI主单位为伏安(VA),工程上也常用千伏安(KVA)。
由于电机和变压器的容量是由它们的额定电压和额定电流来决定的,因此可以用视在功率来表示它们的容量。
视在功率、有功功率与无功功率间,满足下列关系式
图3.45功率三角形
正好构成一个直角三角形(如图3.45所示),称为功率三角形。
例3.25试求图3.46所示电路的有功功率、无功功率和视在功率,其中
尺=2OJR2=1OJC=2mF,L=0.1H,u=502sin100tV。
2
2?
Mt
图3.46例3.25
解:
—jXc(R2+jXl)
Rl'
—jXcR2jXL
=228-15.26门
50.0
22.8-15.26
^2.1915.26
P=UIcos=502.19cos-15.26=105.64W
Q二Ulsin=502.19sin-15.26=-28.82Var
S=UI=502.19=109.5VA
例3.26图3.47所示电路可用于测量线圈的参数R和L。
已测得电压表、电流表和功
率表的读数分别为100V、2A和120W,电源的频率为50Hz,试求R和L。
rvwwx
s
图3.47例3.26
解:
线圈的阻抗模
又有
XL=J|z|2_r2=J502_302=400
所以L==—40—=0.127H
(三)、复功率
为了能够用相量来计算电路的功率,特引入复功率。
在端口电压相量、电流相量分别为
的二端网络中,其复功率定义为:
S=ui(3.61)
式中=I.一“是电流相量I的共轭复数。
复功率的Si主单位为伏安(VA)。
复功率S还可以表示为
S二Ul=u.-入I.一日二UI.九7二UI.二S二Ulcos「jUIsin二PjQ
(3.62)
可见,复功率这个复数的模是网络的视在功率,它的辐角是电压与电流的相位差,它的实部
为有功功率,它的虚部为无功功率。
可以得到,电阻元件的复功率为
S=UIZO°=UI=i2r=u2g
电感元件的复功率为
〜2
S=UIN90°=jUI=jI2Xl
电容元件的复功率为
〜
S=UIN_90°=-jUI=-jl2Xc
在整个电路中,复功率是守恒的,即一些支路发出的复功率一定等于其余支路吸收的复功率。
由复功率守恒,也必然得到有功功率和无功功率是守恒的。
例3.27在图3.48所示电路中,已知R=40iSXl=307,R2=60「,Xc=60,
电源电压US=220・0V。
试求各支路的电流及复功率。
图3.48例3.27
解:
1支路的电流及复功率为
S二Usl=22004"-369=774j581VA
2支路的电流及复功率为
S=U;I;=22002.59/-45=570/-45=403—j403VA
电源支路的电流及复功率为
I=hl2=4.4/-36.92.59亠45=5.42亠8.61A
S=UST=22005.428.61-11928.61=1179j178VA
(四)、功率因数的提高
在正弦交流电路中,由于有功功率
P=UIcos®=Seos®
因此,当负载的功率因数cos:
太低时,电路中电源设备的额定容量就不能充分利用。
P
此外,由于电流I=—,所以当传输的功率、电压一定时,负载的功率因数越低,
Ucos®
则输电线路的电流越大,所引起的线路能量损耗和电压降落越大,影响负载的正常工作。
提高电路的功率因数,就能充分利用电源设备的容量,就能减少输电的电能损耗,改善
供电的电压质量。
一般负载都是电感性的,对于这样的负载,常用电容器与负载并联来提高电路的功率因
数。
可用RL串联表示感性负载,如图3.49(a)所示,画出电路的相量图如图3.49(b)所
示。
在未并电容C时,线路电流「等于负载电流I1,此时功率因数为COS」;并联电容后,
线路电流I=I1I2,功率因数为COS「■。
因为」;•;:
」;,所以COS—•cos「,从而把线路
的功率因数提高。
(a)
(b)
图3.49功率因数的提高
如果要将有功功率为P,端电压为U的负载电路的功率因数由COS「提高到COSX,则所应并联的电容C,可计算如下:
PP
11=,I=
Ucos®Ucos护"
P
丨2=lisin®-IsinW=jy(tan®—tan®J
12==coCU
Xc
代入上式得
P
coCU=—(tan®-tan®”)
U
所以
P
C=r(tan申-tan申")
«U
(3.63)
二、正弦交流电路的相量法
正弦交流电路的分析计算与直流电路的分析计算一样,也是应用基尔霍夫定律和欧姆定
律来进行。
在正弦交流电路中,基尔霍夫定律和欧姆定律的相量形式与直流电路中相应的表达式相似,因而同样可以推出类似于直流电路的分析计算方法。
只要把电路中无源元件用阻
抗或导纳表示,正弦量用相量表示,那么分析计算直流电路的方法都可以推广到正弦交流电路,这样的分析计算方法,称为相量法。
例3.21在图3.40(a)所示电路中,已知R=81,,XC=1O1,
12、I3,并绘出相量图。
u二2202sin•・t60V,试求各支路电流相量h
解
Z1=RjXL=8j6=1036.9「
Z2二-jXC二-j10=10-9011
I=I1I2=2223.122150
=20.2j8.6—19.1j11=1.1j19.6=19.786.8A
(a)
h
ci
(b)
图3.40例3.21图
相量图如图3.40(b)所示。
例3.22在图3.41(a)所示电路中,u=100「2sintV,尺=20「,
4aaa
R2601,试求各支路电流相量I1、I2、I3,并绘出相量图。
oC
=R-i=2011
二R2-jXc=60-j60=602-4511
Z3
二jXL二j60=609011
Ii
(a)(b)
图3.41例3.22图
相量图如图3.41(b)所示。
例3.23在图3.42所示电路中,已知
Usi=2200V,Us2=220/-20V,X“=20",XL2=10」,R=40",试用节点
电压法求各支路电流。
解:
UsiUs22200220-20
ab
—ZlZ2二号“0=213.8-22.8V
丄丄丄丄.丄丄
乙Z2Z3j20j1040
Uab
213.8-22.8
=5.35-22.8A
图3.42例3.23图
在应用相量法时,除用相量解析式计算外,还可利用相量图来分析计算。
例3.24在图3.43(a)所示电路中,已知=l2=10A,U=100V,U与「同
相,试求XL、XC和R。
I=h•12,最后画相量
解以Ubc为参考相量,画在水平方向。
再画相量
U=UabUbc,分别构成两等腰直角三角形,如图3.43(b)所示。
所以
Uab=U=10CM,Ubc二2U=1002VI=21,"0「2A
(b)