m序列产生.doc

m序列产生.doc

《m序列产生.doc》由会员分享，可在线阅读，更多相关《m序列产生.doc（4页珍藏版）》请在冰豆网上搜索。

设计内容及要求

基于MATLAB产生m序列

要求：

1．通过matlab编程产生m序列的产生原理及其产生方法。

2．对特定长度的m序列，分析其性质，及其用来构造其它序列的方法。

第二章m序列设计方案的选择

2.1方案一

MATLAB编程非常简单，无需进行变量声明，可以很方便的实现m序列。

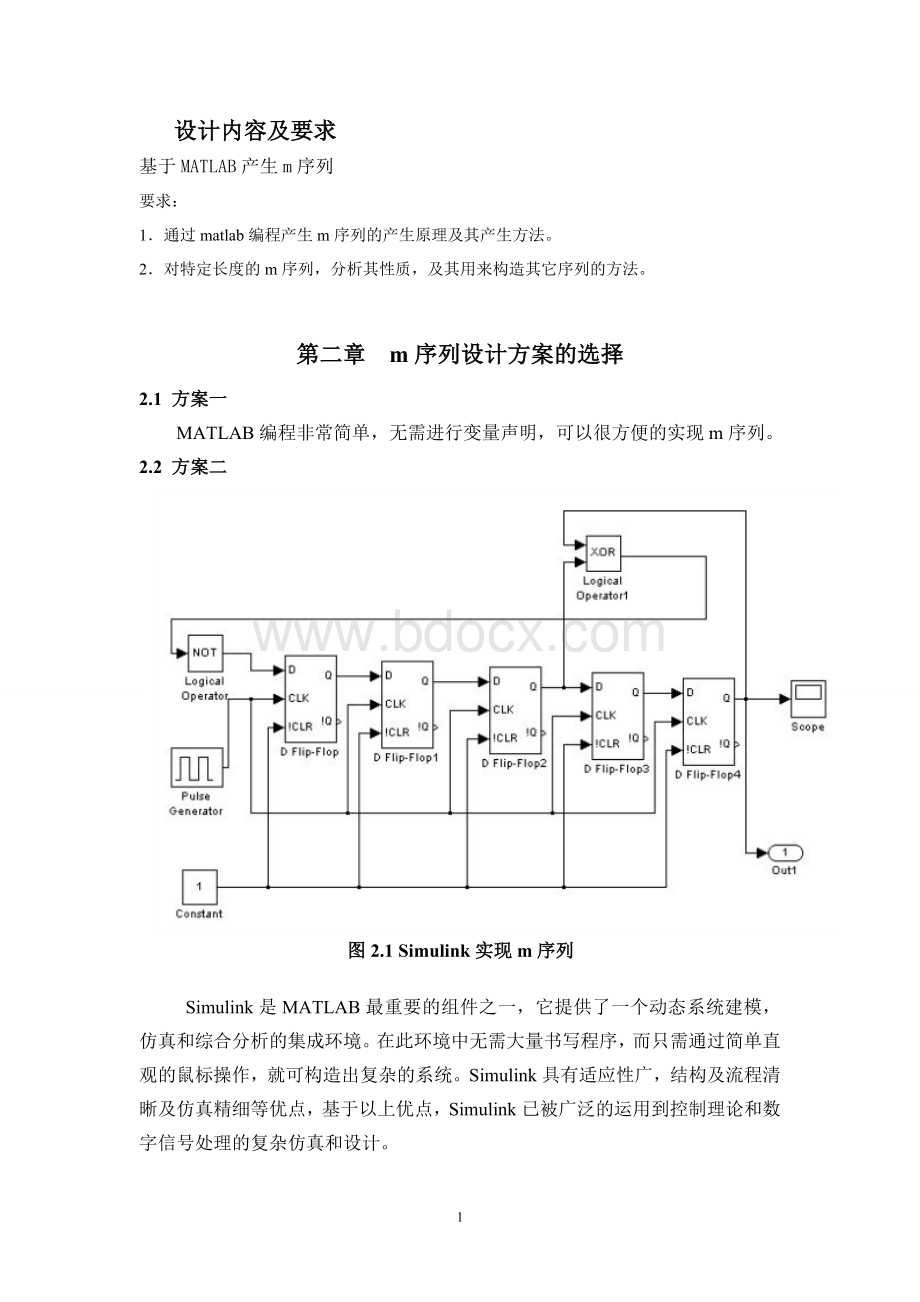
2.2方案二

图2.1Simulink实现m序列

Simulink是MATLAB最重要的组件之一，它提供了一个动态系统建模，仿真和综合分析的集成环境。

在此环境中无需大量书写程序，而只需通过简单直观的鼠标操作，就可构造出复杂的系统。

Simulink具有适应性广，结构及流程清晰及仿真精细等优点，基于以上优点，Simulink已被广泛的运用到控制理论和数字信号处理的复杂仿真和设计。

通过比较方案一和方案二，发现方案一的有点具有通用性而方案二利用MATLAB的Simulink直接搭建模块，在移位寄存器较少的情况下利用此方法比较简单，可是当移位寄存器的个数增多时，要搭建那么多的模块就显的很繁琐了，缺乏通用性，因此本次实验选择方案一。

第三章m序列的产生及性质

3.1m序列的产生原理、结构及产生

m序列是最长线性反馈移位寄存器序列的简称，m序列是由带线性反馈的移位寄存器产生的。

由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器，如果反馈逻辑线路只由模2和构成，则称为线性反馈移位寄存器。

带线性反馈逻辑的移位寄存器设定初始状态后，在时钟触发下，每次移位后各级寄存器会发生变化，其中任何一级寄存器的输出，随着时钟节拍的推移都会产生一个序列，该序列称为移位寄存器序列。

n级线性移位寄存器的如图3.1所示：

图3.1n级线性移位寄存器

图中Ci表示反馈线的两种可能连接方式，Ci=1表示连线接通，第n-i级输出加入反馈中；Ci=0表示连线断开，第n-i级输出未参加反馈。

因此，一般形式的线性反馈逻辑表达式为

------表达式3.1

将等式左边的an移至右边，并将an=C0an（C0=1）带入上式，则上式可以写成

-------表达式3.2

定义一个与上式相对应的多项式

--------表达式3.3

其中x的幂次表示元素的相应位置。

该式为线性反馈移位寄存器的特征多项式，特征多项式与输出序列的周期有密切关系。

当F（x）满足下列三个条件时，就一定能产生m序列：

（1）F（x）是不可约的，即不能再分解多项式；

（2）F（x）可整除xn+1，这里p=2n+1；

（3）F（x）不能整除xn+1，这里q

满足上述条件的多项式称为本原多项式，这样产生m序列的充要条件就变成了如何寻找本原多项式。

根据表9-1中的八进制的反馈系数，可以确定m序列发生器的结构。

以7级m序列反馈系数Ci=（211）8为例，首先将八进制的系数转化为二进制的系数即Ci=（010001001）2，由此我们可以得到各级反馈系数分别为：

C0=1,C1=0,C3=0,C4=0,C5=0,C6=0,C7=1由此就很容易地构造出相应的m序列发生器。

根据反馈系数，其他级数的m序列的构造原理与上述方法相同。

下面通过实例来分析自相关特性

图9-3所示为4级m序列的码序列发生器。

假设初始状态为0001，在时钟脉冲的作

用下，逐次移位。

D3D4作为D1输入，则n＝4码序列产生过程如表9-2所示。

4