练习十磁感应强度洛伦兹力文档格式.docx

资源描述

练习十磁感应强度洛伦兹力文档格式.docx

《练习十磁感应强度洛伦兹力文档格式.docx》由会员分享，可在线阅读，更多相关《练习十磁感应强度洛伦兹力文档格式.docx（45页珍藏版）》请在冰豆网上搜索。

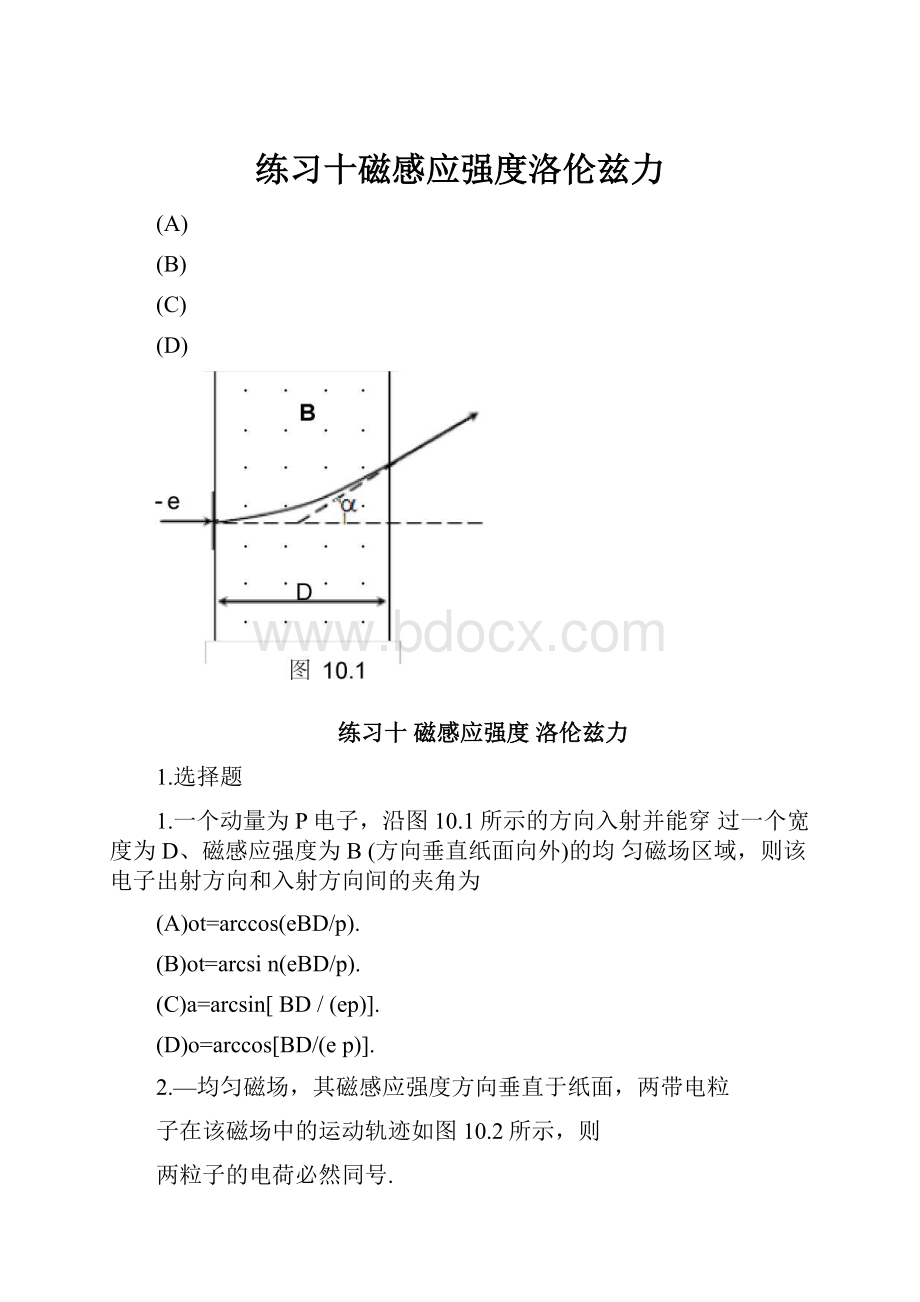
练习十磁感应强度洛伦兹力文档格式.docx

/（eB）

时，（其中me为电子质量，e为电子电量的绝对值，n=1,

2……），电子经过一段飞行后恰好打在图中的O点.

练习十

霍尔效应安培力

图10.6

.选择题

一铜板厚度为D=1.00mm,放置在磁感应强度为B=1.35T的匀强磁场中，磁场方向垂直于导体的侧表面，如图

11.1所示，现测得铜板上下两面电势差为V=1.10X0^V,已知铜板中自由电子数密度n=4.20>

^028m」则此铜板中的电流为

（A）82.2A.（B）54.8A.

（C）30.8A.（D）22.2A.

2.如图11.2,匀强磁场中有一矩形通电线圈，它的平面与磁

场平行，在磁场作用下，线圈发生转动，其方向是

（A）ab边转入纸内

（B）ab边转出纸外

（C）ad边转入纸内

（D）ad边转出纸外

（D）（R2+R1）1（3d）.

5通有电流I的正方形线圈MNOP，边长为a（如图11.5）,放置在均匀磁场中，已知磁感应强度B沿Z轴方向，则线圈所受的磁力矩M为

IaB，沿y负方向.

IaB/2，沿z方向.

IaB，沿y方向.

IaB/2,沿y方向.

二.填空题

1.如图11.6所示，在真空中有一半径为a的3/4园弧形的导线，其

中通以稳恒电流I,导线置于均匀外磁场B中，且B与导线所在平面垂直，则该圆弧载流导线be所受的磁力大小为.

2.平面线圈的磁矩

圈

法则，当四指的方向代表

表方向.

Pm=ISn，其中S是电流为I的平面线,n是线圈的;

按右手螺旋

方向时，大姆指的方向代

绕过圆心且垂直盘面的

—个半径为R、电荷面密度为O的均匀带电圆盘，以角速度

轴线AA旋转，今将其放入磁感应强度为B的均匀外磁场中，B的方向垂直于轴线AA，在距盘心为r处取一宽为dr的与盘同心的圆环，贝恫环内相当于有电流，

该微元电流环磁矩的大小为,该微元电流环所受磁力矩的大小

为，圆盘所受合力矩的大小为.

三•计算题

1.在霍耳效应实验中，宽1.0em，长4.0cm，厚1.0X0'

em的导体，沿长度方向载有

3.0A的电流，此导体片放在与其垂直的匀强磁场（B=1.5T）中，产生1.0X0*V的横向电压,

（3）假设载流子

试由这些数据求：

（1）载流子的漂移速度；

（2）每立方厘米的载流子数目；

是电子，试就此题作图，画出电流方向、磁场方向及霍耳电压的极性.

2如图11.7所示，水平面内有一圆形导体轨道，匀强磁场B的方

向与水平面垂直，一金属杆0M（质量为m）可在轨道上绕0运转,轨道半径为a.若金属杆与轨道的摩擦力正比于M点的速度，比例系

数为k,试求

（1）若保持回路中的电流不变，开始时金属杆处于静止，则t时刻金属杆的角速度等于多少？

（2）为使金属杆不动，

在M点应加多少的切向力.

图11.7

练习十二毕奥一萨伐尔定律

•选择题

1.宽为a，厚度可以忽略不计的无限长扁平载流金属片，如图12.1所示，中心轴线上方一点P的磁感应强度

的方向是

（A）沿y轴正向.

沿z轴负向.

沿y轴负向.沿x轴正向.

（A）72円I

（2

a）,在yz面内，

与

y成45

角.

（B）72比I

y成135

（C）72比I

a）,在xy面内，

x成45

（D）血比I

a）,在zx面内，

z成45

3.—无限长载流导线，

弯成如图12.3所示的形状，

其中

BCD弧是半径为

R的半圆弧，DE段平

2.两无限长载流导线，如图12.2放置，则坐标原点的磁

感应强度的大小和方向分别为：

ABCD段在xOy平面内，

行于Oz轴，则圆心处的磁感应强度为

（A）（4R）].

（4R）].

（B）j比I

4.一电流兀

（4

R）

+k[%I

—k[此I

+k[比

R）—%

R）+Po

R）—比I（4R）].

I位于直角坐标系原点，电流沿Z轴方向，空间点

R）—k[AoI

图

12.3

-R

P（x,y,z）的磁感应强

度沿x轴的分量是：

（A）0.

（B）-（

（C）-（

（D）-（

5.电流I

）iy

）ix

/222、3/2

（x+y+z）.

222、3/2

222、

bc边方向经a点流入一电阻

由长直导线

均匀分布的正三角形线框

直导线2返回电源（如图12.4），若载流直导线1、2和三角形

1沿垂直

，再由b点沿垂直ac边方向流出，经长

框在框中心0点产生的磁感应强度分别用B1、B2和B3表示,则0点的磁感应强度大小

（A）B=0，因为B1=B2=B3=0.

（B）B=0,因为虽然B1

（C）B

（D）B

0，因为虽然

0,B20,但B1+B2=0,B3=0.

B3=0,但B1+B2B1+B2=0,但B3

图12.4

1.氢原子中的电子，以速度v在半径r的圆周上作匀速圆周运动，它等效于一圆电流，

其电流I用v、r、e（电子电量）表示的关系式为I=，此圆电流在中心产生

的磁场为B=，它的磁矩为Pm=_

2.真空中稳恒电流I流过两个半径分别为R1、R2的同心半圆形导线，两半圆导线间由沿直径的直导线连接，电流沿直导线流入

（1）如果两个半圆面共面，如图12.5

（1），

心2b

图12.6

圆心O点磁感应强度Bo的大小为，方向为;

（2）如果两个半圆面正交，如图12.5

（2），则圆心O点磁感应强度

Bo的大小为,B0的方向与y轴的夹角

为.

3.在真空中，电流由长直导线1沿半径方向经a点流入一电阻均匀分布的圆环再由b点沿切向流出，经长直导线2返回电源（如图12.6）,已知直导线上的电流强度为I，圆环半径为R上aOb=90。

则圆心0点处的

磁感应强度的大小B=.

计算题

1.一半径R=1.0cm的无限长1/4圆柱面形金属片，沿轴向通有电流

1=10.0A的电流，设电流在金属片上均匀分布，试求圆柱轴线上任意一

点P的磁感应强度.

2.如图12.6,将一导线由内向外密绕成内半径为R1,外半径为R2

的园形平面线圈，共有N匝，设电流为I，求此园形平面载流线圈在中

心0处产生的磁感应强度的大小.

练习十三毕奥一萨伐尔定律（续）安培环路定律

一.选择题

1.图13.1为磁场B中的一袋形曲面，曲面的边缘为一半径等于R的圆，此圆面的平面与磁感应强度B的方向成/6角，

此袋形曲面的磁通量m（设袋形曲面的法线向外）为

r2b.

R2B/2.

R2B2.

（B）73

（C）-

则

13.2所示，XY平面内有两相距为流导线，电流的大小相等，方向相同且平行于原点均为a,Z轴上有一点感应强度B

大小为^^1

大小为卩01

大小为卩0|

大小为MdI

2.如图

P距两电流均为

L的无限长直载

X轴，距坐标2a,贝yP点的磁

3.如图13.3所示的电路

/（8R）.

/（4R）.

/（2R）.

Ii穿过一回路I

Z轴正向.

（4a）,方向沿

a）,方向沿Z轴正向.

（4a）,方向沿丫轴正向.

（4a）,方向沿丫轴负向.

，设线圈导线的截面积相同，材料相同，则0点处磁感应强度大小为

图13.3

，而电流12则在回路的外面，于是有

（A）I上各点的

B及积分

（B）I上各点的

B只与l1

护dl都只与|1有关.有关，积分ufB'

dl与|1、12有关.

（C）I上各点的

B与Ii、

I2有关，积分cfBdl与I2无关.

（D）I上各点的

B及积分dl都与li、

I2有关.

5.对于某一回路

回路

I，积分cjBdl等于零,内一定有电流.内可能有电流.内一定无电流.

内可能有电流，但代数和为零

则可以断定

1.其圆心重合，相互正交的，半径均为

I,且接触点处相互绝缘，如图13.4所示，则圆心0处磁感应强度的矢量式为.

R的两平面圆形线圈，匝数均为N,电流均为

2.一带正电荷q的粒子以速率v从X负方向飞过来向X正方向飞去，当它经过坐标原

点时，在X轴上的X0处的磁感应强度矢量表达式为，在丫轴上的yo处的磁

感应强度矢量表达式为.

3.如图13.5所示，真空中有两圆形电流11和12和三个环路L1L2L3,则安培环路定

律的表达式为qB.dl=,qBdl=

dl=

1.在一半径R=1.0cm的无限长半圆柱面形金

属薄片中，自上而下地有I=5.0A的电流通过，如图

13.6所示，试求圆柱轴线上任意一点P的磁感应强度

B的大小及方向.

2.试用安培环路定律和磁场的高斯定理证明磁

力线处处平行的无电流空间的磁场为匀强磁场.

13.5

」

图13.6

练习十四安培环路定律（续）变化电场激发的磁场

4.位移电流与传导电流一样

都是由载流子的定向移动产生的;

都可以激发磁场；

都可以用电流表测量其大小；

都一样产生热效应.

2.如图14.1所示,有两根无限长直载流导线平行放置，电流分别为l1和l2,L是空间一闭曲

线,11在L内,12在L外,P是L上的一点，今将12在L外向l1移近时，则有

（A）1Bdl与Bp同时改变.

qBdl与Bp都不改变.qBdl不变,Bp改变.cfBdl改变,Bp不变.

3.如图14.2,—环形电流I和一回路I，则积分cfBdl应等于

2I.

-2止I

2比1.

4.对于某一回路I，积分qB”dl=卩0|工0,则可以肯定

B可能为零，有些可能不为零，或所有点可能全不为零B一定不为零.

B一定为零.

B可能都为零.

14.3中的哪一图

5.载流空心圆柱导体的内外半径分别为点的B—r曲线应为图

b电流在导体截面上均匀分布，则空间各

图14.3

图14.4

器,放在真空中，今对电容器匀速充电，使两板间电场的变化率为dE/dt=1.0x1013Vm-1s-1,则两板

间位移电流的大小为板间一点P距中心线为r=0.05m,则P点处的磁感应强度

为Bp=三.计算题

略不计，今将电容两极板以速率v匀速拉开，当两极板间距为x时，求电容器内位移电流密

度的大小和方向.

2.图14.6所示是一根外半径为R1的无限长圆柱形导体管的横截面，管内空心部分的半径为R2，空心部分的轴与圆柱的轴相平行但不重合，两轴间的距离为a,且a〉R2，现有

电流I沿导体管流动，电流均匀分布在管的横截面上，电流方向与管的轴线平行，求

（1）

圆柱轴线上的磁感应强度的大小；

（2）空心部分轴线上的磁感应强度的大小；

（3）设R1=10mm,

R2=0.5mm,a=5.0mm,l=20A,分别计算上述两处磁感应强度的大小.

只与磁化电流产生的磁场有关.

与外磁场和磁化电流产生的场有关.

只与外磁场有关.

只与介质本身的性质有关，与磁场无关

5.以下说法中正确的是

若闭曲线L内没有包围传导电流，则曲线L上各点的H必等于零;

对于抗磁质，B与H—定同向；

H仅与传导电流有关；

闭曲线L上各点H为零，则该曲线所包围的传导电流的代数和必为零.

1.如图15.1所示的两种不同铁磁质的磁滞回线中，适合制造永久磁铁的是磁介质，适合制造变压器铁芯的是磁介质.

2.一个绕有500匝导线的平均周长50cm的细环，载有0.3A电流时，铁芯的相对磁导率

为600

（1）铁芯中的磁感应强度B为;

（2）铁芯中的磁场强度H为.

的关

图15.2中为三种不同的磁介质的B〜H关系曲线，其中虚线表示的是

系，说明a、b、c各代表哪一类磁介质的B〜H关系曲线：

练习十六静磁场习题课

2.在磁场方向和导体中电流方向不变的条件下

（正负）无关，产生霍耳电压的

导体中的载流子所受磁场力的方向与载流子的种类正负与载流子的种类有关.

（B）导体中的载流子所受磁场力的方向与载流子的种类（正负）无关，产生霍耳电压的

正负与载流子的种类无关

（C）导体中的载流子所受磁场力的方向与载流子的种类正负与载流子的种类无关.

（D）导体中的载流子所受磁场力的方向与载流子的种类正负与载流子的种类有关.

（正负）

有关，产生霍耳电压的

3.在磁场方向和导体中电流方向不变的条件下

（A）导体中的载流子所受磁场力的方向与载流子的种类

力的方向与载流子的种类有关.

（B）导体中的载流子所受磁场力的方向与载流子的种类

（C）导体中的载流子所受磁场力的方向与载流子的种类

力的方向与载流子的种类无关.

（D）导体中的载流子所受磁场力的方向与载流子的种类

4.无限长直电流产生磁场的公式为B=0I（2r）,以下说法正确的是

此公式中只要求导线为直导线；

此公式中只要求导线为无限长，且截面必须为圆形；

当r=0时，此公式不适用，因为磁感强度B为无限大；

当r=0时，此公式不适用，因为此时场点到导线的距离不是远大于导线的截面尺

无关，导线所受的安培

有关，导线所受的安培

寸，导线不能看成无限细.

5.安培环路定律qBdl=皿中的电流I

必须穿过回路必须穿过回路不必穿过回路必须穿过回路

I所圆的曲面,

1.图16.1示为磁场中的通电薄金属

板，当磁感强度B沿X轴负向，电流I沿丫正向时，则金属板中对应于霍尔电场的电场强度EH的方向沿.

2.如图16.2，均匀磁场中放一均匀带

正电荷的圆环，其电荷线密度为，圆环可绕与环面垂直的轴旋

转，当圆环以角速度转动时，圆环受到的磁力矩的大小

为，其方向为.

16.1

7/'

■

丿

3.在氢原子中，若视电子（质量为m,电量为F）绕质子作半径为r，角速度为动所等效的环形电流

的匀速圆周运动，那么，电子作匀速圆周运

；

电子的轨道磁矩为

图16.2

Pm=

1.有一根质量为m的倒U形导线，两端浸没在水银槽中,

中，如图16.3，如果使一个电流脉冲，即电量电流脉冲的持续时间t同导线跳起来的时间

流脉冲的大小，设B=0.1T,m=1CK103kg,l=0.2m,h=0.3m.（提示：

利用动量原理求冲量，并找出Jidt与冲量jFdt的关系）

2.如图16.4所示，将一无限大均匀载流平面放入均匀磁场中，（设均匀磁场方向沿

导线的上段I处于均匀磁场Bq=Jidt通过导线，这导线就会跳起来，假定t相比为非常小，试由导线所达高度h计算电

OX轴正方向）且其电流方向与磁场方向垂直指向纸内，已知放入后平面两侧的总磁感应强度分别为B1与B2,求：

图16.3

（1）原磁场的磁感应强度B0及此无限大均匀载流平面激发磁场的磁感应强度

（2）

（3）

此无限大均匀载流平面的面电流的线密度J;

该载流平面上单位面积所受的磁场力大小及方向

练习十七电磁感应定律动生电动势

1在一线圈回路中，规定满足如图17.1所示的旋转方向时，

值。

若磁铁沿箭头方向进入线圈，则有

（A）d①/dt<

0,£

（B）d①/dt>

0,z<

（C）d①/dt>

0,z>

（D）d①/dt<

2.—磁铁朝线圈运动，如图17.2所示，则线圈内的感应

电流的方向（以螺线管内流向为准）以及电表两端电位Ua

和Ub的高低为：

I由A到B,Ua>

Ub.

I由B至UA,

I由B至UA,I由A至UB,

电动势

磁通量①为正

图17.1

Ua<

Ua>

Ub.

单位长度匝数为nR的测量线圈，如图

图17.2

电流为I，其中部放一面积为A,

17.3所示，开始时螺线管与测

180。

，则通过测量线圈某导线

3.—长直螺线管，总匝数为N，电阻为量线圈的轴线平行，若将测量线圈翻转截面上的电量q为

（A）2onINA/R.（B）onINA/R.

（C）0NIA/R.（D）onlA/R.

4.若尺寸相同的铁环与铜环所包围的面积中穿过相同变化率的磁通量，则在两环中

（A）感应电动势不同，感应电流相同.

（B）感应电动势相同，感应电流也相同.

图17.3

（C）感应电动势不同，感应电流也不同

（D）感应电动势相同，感应电流不同.

5.如17.4图，当无限长直电流旁的边长为

da与I平行）以速率V向右运动时，则某时刻（此时ad距I为r）及感应电流的流向是：

名=A0lvl，电流流向dTAbTa.

l的正方形回路abcda（回路与I共面且be、

回路的感应电动势的大小

2兀r

Aolvl

Ivl2

=，电流流向d—ja.

2ir（r+I）

4Ivl2

=，电流流向a—、b_、e—、d

2兀r（r+丨）

电流流向d.

图17.4

17.5所示，一光滑的金属导轨置于均匀磁场B中，导

I，可在导轨上平行移动，速度为V，则回路中的感应

Ub（填），回路中

线ab长为

电动势=，Ua

的电流1=，电阻R上消耗的功率P=

2.如图17.6所示，长为I的导体棒AB在均匀磁场B中绕通过

的轴00转动，AC长为I3，贝UUb—Ua=

—Uc=,Ub—Uc=

图所示的位置时,B点的运动方向向里.）

3.如图17.7所示，直角三角形金属框

平行于PQ,当金属框绕PQ以角速度

的大小i=方向

势大小i=.（当金属框运动到如图所示的位置时

的运动方向向里.）

•b-

图17.5

C点

.（当导体棒运动到如

0AI半.I/3AC21/3

PQS置于匀强磁场B中,转动时，PS边感应电动势—，整个回路的感应电动

$点

1.半径为R的四分之一圆弧导线位于均匀磁场B中,圆弧的a端与圆心0的连线垂直于

磁场，今以aO为轴让圆弧ae以角速度旋转，当转到如图17.8所示的位置时（此时e点的

运动方向向里），求导线圆弧上的感应电动势.

2.有一很长的长方形的U形导轨，宽

为丨，竖直放置，裸导线ab可沿金属导轨

（电阻忽略）无摩擦地下滑，导轨位于磁

感应强度B水平均匀磁场中，如图17.9所示，设导线电阻为R,试求：

导线数关系.

ab的质量为m,它在电路中的abcd形成回路，t=0时，V=0，ab下滑的速度V与时间t的函

图17.8

XXXX

XXX

展开阅读全文