知识梳理与自测人教A版文科数学《 84直线平面平行的判定与性质》Word文件下载.docx

知识梳理与自测人教A版文科数学《 84直线平面平行的判定与性质》Word文件下载.docx

《知识梳理与自测人教A版文科数学《 84直线平面平行的判定与性质》Word文件下载.docx》由会员分享，可在线阅读，更多相关《知识梳理与自测人教A版文科数学《 84直线平面平行的判定与性质》Word文件下载.docx（26页珍藏版）》请在冰豆网上搜索。

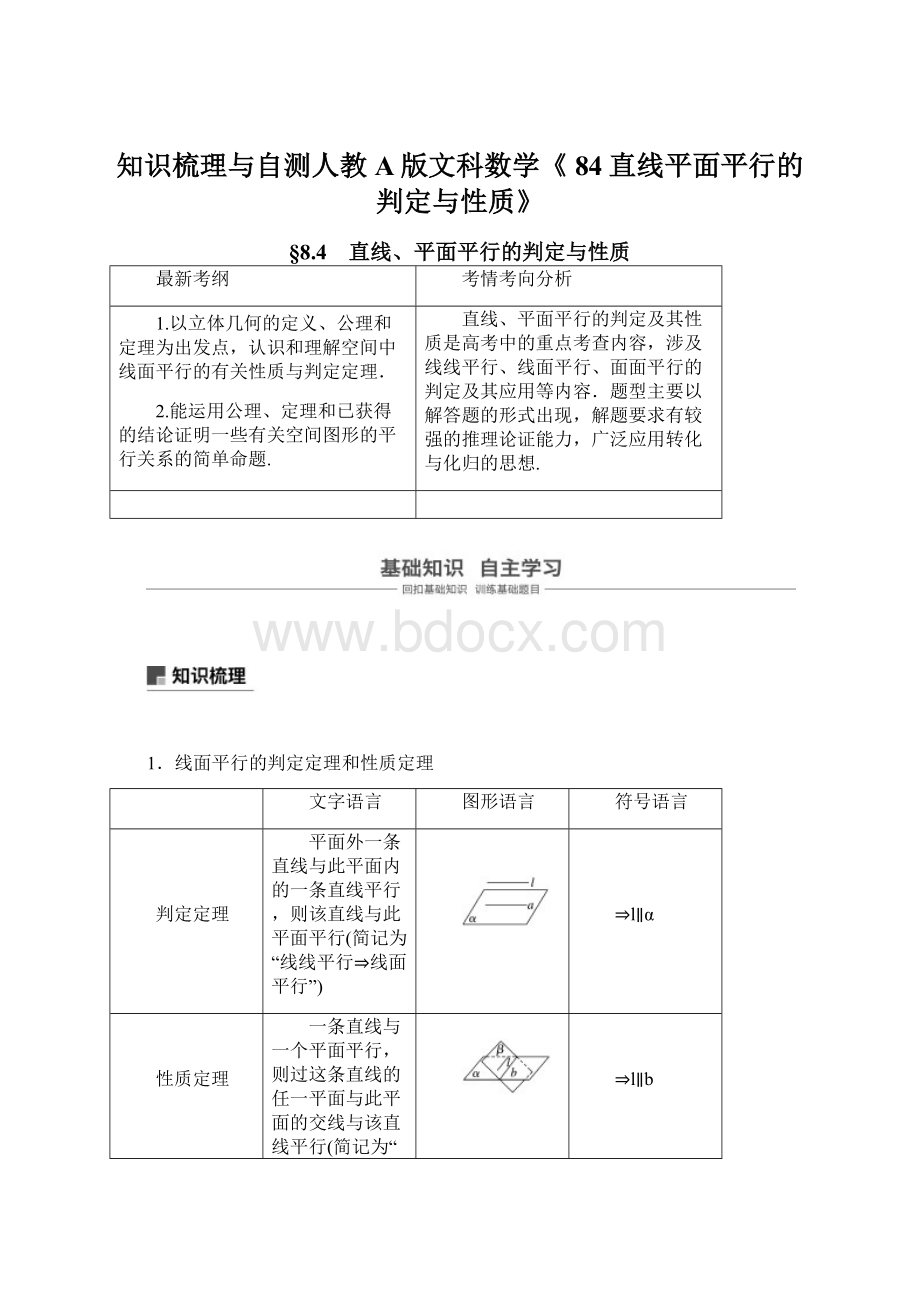
答案　D

解析　若α∩β＝l，a∥l，a⊄α，a⊄β，则a∥α，a∥β，故排除A.若α∩β＝l，a⊂α，a∥l，则a∥β，故排除B.若α∩β＝l，a⊂α，a∥l，b⊂β，b∥l，则a∥β，b∥α，故排除C.故选D.

3．[P62A组T3]如图，在正方体ABCD－A1B1C1D1中，E为DD1的中点，则BD1与平面AEC的位置关系为________．

答案　平行

解析　连接BD，设BD∩AC＝O，连接EO，

在△BDD1中，E为DD1的中点，O为BD的中点，

所以EO为△BDD1的中位线，则BD1∥EO，

而BD1⊄平面ACE，EO⊂平面ACE，

所以BD1∥平面ACE.

题组三　易错自纠

4．（2019·

荆州模拟）对于空间中的两条直线m，n和一个平面α，下列命题中的真命题是（　　）

A．若m∥α，n∥α，则m∥n

B．若m∥α，n⊂α，则m∥n

C．若m∥α，n⊥α，则m∥n

D．若m⊥α，n⊥α，则m∥n

解析　对A，直线m，n可能平行、异面或相交，故A错误；

对B，直线m与n可能平行，也可能异面，故B错误；

对C，m与n垂直而非平行，故C错误；

对D，垂直于同一平面的两直线平行，故D正确．

5．若平面α∥平面β，直线a∥平面α，点B∈β，则在平面β内且过B点的所有直线中（　　）

A．不一定存在与a平行的直线

B．只有两条与a平行的直线

C．存在无数条与a平行的直线

D．存在唯一与a平行的直线

答案　A

解析　当直线a在平面β内且过B点时，不存在与a平行的直线，故选A.

6．设α，β，γ为三个不同的平面，a，b为直线，给出下列条件：

①a⊂α，b⊂β，a∥β，b∥α；

②α∥γ，β∥γ；

③α⊥γ，β⊥γ；

④a⊥α，b⊥β，a∥b.

其中能推出α∥β的条件是______．（填上所有正确的序号）

答案　②④

解析　在条件①或条件③中，α∥β或α与β相交；

由α∥γ，β∥γ⇒α∥β，条件②满足；

在④中，a⊥α，a∥b⇒b⊥α，又b⊥β，从而α∥β，④满足．

题型一　直线与平面平行的判定与性质

命题点1　直线与平面平行的判定

例1如图，在几何体ABCDE中，四边形ABCD是矩形，AB⊥平面BEC，BE⊥EC，AB＝BE＝EC＝2，G，F分别是线段BE，DC的中点．

求证：

GF∥平面ADE.

证明　方法一　如图，取AE的中点H，连接HG，HD，

又G是BE的中点，

所以GH∥AB，且GH＝AB.

又F是CD的中点，

所以DF＝CD.

由四边形ABCD是矩形得

AB∥CD，AB＝CD，

所以GH∥DF，且GH＝DF，

从而四边形HGFD是平行四边形，

所以GF∥DH.

又DH⊂平面ADE，GF⊄平面ADE，

所以GF∥平面ADE.

方法二　如图，取AB的中点M，连接MG，MF.

又G是BE的中点，可知GM∥AE.

又AE⊂平面ADE，GM⊄平面ADE，

所以GM∥平面ADE.

在矩形ABCD中，

由M，F分别是AB，CD的中点得MF∥AD.

又AD⊂平面ADE，MF⊄平面ADE.

所以MF∥平面ADE.

又因为GM∩MF＝M，GM⊂平面GMF，MF⊂平面GMF，

所以平面GMF∥平面ADE.

因为GF⊂平面GMF，

命题点2　直线与平面平行的性质

例2（2019·

东三省四市教研联合体模拟）在如图所示的几何体中，四边形ABCD是正方形，PA⊥平面ABCD，E，F分别是线段AD，PB的中点，PA＝AB＝1.

（1）证明：

EF∥平面PDC；

（2）求点F到平面PDC的距离．

（1）证明　取PC的中点M，连接DM，MF，

∵M，F分别是PC，PB的中点，

∴MF∥CB，MF＝CB，

∵E为DA的中点，四边形ABCD为正方形，

∴DE∥CB，DE＝CB，

∴MF∥DE，MF＝DE，∴四边形DEFM为平行四边形，

∴EF∥DM，

∵EF⊄平面PDC，DM⊂平面PDC，

∴EF∥平面PDC.

（2）解　∵EF∥平面PDC，∴点F到平面PDC的距离等于点E到平面PDC的距离．

∵PA⊥平面ABCD，∴PA⊥DA，

在Rt△PAD中，PA＝AD＝1，∴DP＝，

∵PA⊥平面ABCD，∴PA⊥CB，

∵CB⊥AB，PA∩AB＝A，PA，AB⊂平面PAB，

∴CB⊥平面PAB，

∴CB⊥PB，则PC＝，

∴PD2＋DC2＝PC2，

∴△PDC为直角三角形，其中PD⊥CD，

∴S△PDC＝×

1×

＝，

连接EP，EC，易知VE－PDC＝VC－PDE，

设E到平面PDC的距离为h，

∵CD⊥AD，CD⊥PA，AD∩PA＝A，AD，PA⊂平面PAD，

∴CD⊥平面PAD，

则×

h×

＝×

×

1，

∴h＝，∴F到平面PDC的距离为.

思维升华判断或证明线面平行的常用方法

（1）利用线面平行的定义（无公共点）．

（2）利用线面平行的判定定理（a⊄α，b⊂α，a∥b⇒a∥α）．

（3）利用面面平行的性质（α∥β，a⊂α⇒a∥β）．

（4）利用面面平行的性质（α∥β，a⊄β，a∥α⇒a∥β）．

跟踪训练1（2019·

崇左联考）如图，在四棱锥P－ABCD中，平面PAC⊥平面ABCD，且PA⊥AC，PA＝AD＝2，四边形ABCD满足BC∥AD，AB⊥AD，AB＝BC＝1.点E，F分别为侧棱PB，PC上的点，且＝＝λ（λ≠0）．

（1）求证：

EF∥平面PAD；

（2）当λ＝时，求点D到平面AFB的距离．

（1）证明　∵＝＝λ（λ≠0），∴EF∥BC.

∵BC∥AD，∴EF∥AD.

又EF⊄平面PAD，AD⊂平面PAD，

∴EF∥平面PAD.

（2）解　∵λ＝，

∴F是PC的中点，

在Rt△PAC中，PA＝2，AC＝，

∴PC＝＝，

∴PF＝PC＝.

∵平面PAC⊥平面ABCD，且平面PAC∩平面ABCD＝AC，PA⊥AC，PA⊂平面PAC，

∴PA⊥平面ABCD，∴PA⊥BC.

又AB⊥AD，BC∥AD，∴BC⊥AB，

又PA∩AB＝A，PA，AB⊂平面PAB，

∴BC⊥平面PAB，

∴BC⊥PB，∴在Rt△PBC中，BF＝PC＝.

连接BD，DF，设点D到平面AFB的距离为d，

在等腰三角形BAF中，BF＝AF＝，AB＝1，

∴S△ABF＝，

又S△ABD＝1，点F到平面ABD的距离为1，

∴由VF－ABD＝VD－AFB，得×

1＝×

d×

，

解得d＝，即点D到平面AFB的距离为.

题型二　平面与平面平行的判定与性质

例3如图所示，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：

（1）B，C，H，G四点共面；

（2）平面EFA1∥平面BCHG.

证明　

（1）∵G，H分别是A1B1，A1C1的中点，

∴GH是△A1B1C1的中位线，

∴GH∥B1C1.

又∵B1C1∥BC，∴GH∥BC，

∴B，C，H，G四点共面．

（2）∵E，F分别是AB，AC的中点，

∴EF∥BC.

∵EF⊄平面BCHG，BC⊂平面BCHG，

∴EF∥平面BCHG.

又G，E分别为A1B1，AB的中点，A1B1∥AB且A1B1＝AB，

∴A1G∥EB，A1G＝EB，

∴四边形A1EBG是平行四边形，

∴A1E∥GB.

又∵A1E⊄平面BCHG，GB⊂平面BCHG，

∴A1E∥平面BCHG.

又∵A1E∩EF＝E，A1E，EF⊂平面EFA1，

∴平面EFA1∥平面BCHG.

引申探究

1．在本例中，若将条件“E，F，G，H分别是AB，AC，A1B1，A1C1的中点”变为“D1，D分别为B1C1，BC的中点”，求证：

平面A1BD1∥平面AC1D.

证明　如图所示，连接A1C，AC1，交于点M，

∵四边形A1ACC1是平行四边形，

∴M是A1C的中点，连接MD，

∵D为BC的中点，

∴A1B∥DM.

∵A1B⊂平面A1BD1，DM⊄平面A1BD1，

∴DM∥平面A1BD1，

又由三棱柱的性质知，D1C1∥BD且D1C1＝BD，

∴四边形BDC1D1为平行四边形，

∴DC1∥BD1.

又DC1⊄平面A1BD1，BD1⊂平面A1BD1，

∴DC1∥平面A1BD1，

又DC1∩DM＝D，DC1，DM⊂平面AC1D，

因此平面A1BD1∥平面AC1D.

2．在本例中，若将条件“E，F，G，H分别是AB，AC，A1B1，A1C1的中点”变为“点D，D1分别是AC，A1C1上的点，且平面BC1D∥平面AB1D1”，试求的值．

解　连接A1B，AB1，交于点O，连接OD1.

由平面BC1D∥平面AB1D1，

且平面A1BC1∩平面BC1D＝BC1，平面A1BC1∩平面AB1D1＝D1O，

所以BC1∥D1O，则＝＝1.

同理，AD1∥C1D，

又AD∥C1D1，

所以四边形ADC1D1是平行四边形，

所以AD＝D1C1，

又AC＝A1C1，

所以＝，所以＝1，即＝1.

思维升华证明面面平行的方法

（1）面面平行的定义．

（2）面面平行的判定定理．

（3）垂直于同一条直线的两个平面平行．

（4）两个平面同时平行于第三个平面，那么这两个平面平行．

（5）利用“线线平行”、“线面平行”、“面面平行”的相互转化．

跟踪训练2（2018·

合肥质检）如图，在多面体ABCDEF中，四边形ABCD是正方形，BF⊥平面ABCD，DE⊥平面ABCD，BF＝DE，M为棱AE的中点．

平面BDM∥平面EFC；

（2）若AB＝1，BF＝2，求三棱锥A－CEF的体积．

（1）证明　如图，设AC与BD交于点N，

则N为AC的中点，连接MN，

又M为棱AE的中点，

∴MN∥EC.

∵MN⊄平面EFC，EC⊂平面EFC，

∴MN∥平面EFC.

∵BF⊥平面ABCD，DE⊥平面ABCD，且BF＝DE，

∴BF∥DE且BF＝DE，

∴四边形BDEF为平行四边形，

∴BD∥EF.

∵BD⊄平面EFC，EF⊂平面EFC，

∴BD∥平面EFC.

又MN∩BD＝N，MN，BD⊂平面BDM，

∴平面BDM∥平面EFC.

（2）解　连接EN，FN.

在正方形ABCD中，AC⊥BD，

又BF⊥平面ABCD，∴BF⊥AC.

又BF∩BD＝B，BF，BD⊂平面BDEF，

∴AC⊥平面BDEF，

又N是AC的中点，

∴V三棱锥A－NEF＝V三棱锥C－NEF，

∴V三棱锥A－CEF＝2V三棱锥A－NEF＝2×

AN×

S△NEF＝2×

2＝，

∴三棱锥A－CEF的体积为.

题型三　平行关系的综合应用

例4如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．

AB∥平面EFGH，CD∥平面EFGH；

（2）若AB＝4，CD＝6，求四边形EFGH周长的取值范围．

（1）证明　∵四边形EFGH为平行四边形，

∴EF∥HG.

∵HG⊂平面ABD，EF⊄平面ABD，

∴EF∥平面ABD.

又∵EF⊂平面ABC，平面ABD∩平面ABC＝AB，

∴EF∥AB，又∵AB⊄平面EFGH，EF⊂平面EFGH，

∴AB∥平面EFGH.同理可证，CD∥平面EFGH.

（2）解　设EF＝x（0<

x<

4），

∵EF∥AB，FG∥CD，

∴＝，则＝＝＝1－.

∴FG＝6－x.

∵四边形EFGH为平行四边形，

∴四边形EFGH的周长l＝2＝12－x.

又∵0<

4，∴8<

l<

12，

即四边形EFGH周长的取值范围是（8,12）．

思维升华利用线面平行的性质，可以实现与线线平行的转化，尤其在截面图的画法中，常用来确定交线的位置，对于最值问题，常用函数思想来解决．

跟踪训练3如图，E是正方体ABCD－A1B1C1D1的棱DD1的中点，过A，C，E三点作平面α与正方体的面相交．

（1）画出平面α与正方体ABCD－A1B1C1D1各面的交线；

（2）求证：

BD1∥平面α.

（1）解　如图，交线即为EC，AC，AE，平面α即为平面AEC.

（2）证明　连接AC，BD，设BD与AC交于点O，连接EO，

∵四边形ABCD为正方形，∴O是BD的中点，

又E为DD1的中点．

∴OE∥BD1，又OE⊂平面α，BD1⊄平面α.

∴BD1∥平面α.

1．下列命题中正确的是（　　）

A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面

B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行

C．平行于同一条直线的两个平面平行

D．若直线a，b和平面α满足a∥b，a∥α，b⊄α，则b∥α

解析　A中，a可以在过b的平面内；

B中，a与α内的直线也可能异面；

C中，两平面可相交；

D中，由直线与平面平行的判定定理知b∥α，正确．

2．已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是（　　）

A．若α，β垂直于同一平面，则α与β平行

B．若m，n平行于同一平面，则m与n平行

C．若α，β不平行，则在α内不存在与β平行的直线

D．若m，n不平行，则m与n不可能垂直于同一平面

解析　A项，α，β可能相交，故错误；

B项，直线m，n的位置关系不确定，可能相交、平行或异面，故错误；

C项，若m⊂α，α∩β＝n，m∥n，则m∥β，故错误；

D项，假设m，n垂直于同一平面，则必有m∥n，所以原命题正确，故D项正确．

3．（2019·

济南模拟）如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB的位置关系是（　　）

A．异面

B．平行

C．相交

D．以上均有可能

答案　B

解析　在三棱柱ABC－A1B1C1中，AB∥A1B1.

∵AB⊂平面ABC，A1B1⊄平面ABC，

∴A1B1∥平面ABC.

∵过A1B1的平面与平面ABC交于DE，

∴DE∥A1B1，∴DE∥AB.

4．（2018·

大同模拟）若平面α截三棱锥所得截面为平行四边形，则该三棱锥与平面α平行的棱有（　　）

A．0条B．1条

C．2条D．0条或2条

答案　C

解析　如图，设平面α截三棱锥所得的四边形EFGH是平行四边形，

则EF∥GH，EF⊄平面BCD，GH⊂平面BCD，

所以EF∥平面BCD，

又EF⊂平面ACD，平面ACD∩平面BCD＝CD，

则EF∥CD，EF⊂平面EFGH，CD⊄平面EFGH，

则CD∥平面EFGH，

同理AB∥平面EFGH，

所以该三棱锥与平面α平行的棱有2条，故选C.

5．（2017·

全国Ⅰ）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（　　）

解析　A项，作如图①所示的辅助线，其中D为BC的中点，则QD∥AB.

∵QD∩平面MNQ＝Q，∴QD与平面MNQ相交，

∴直线AB与平面MNQ相交；

B项，作如图②所示的辅助线，则AB∥CD，CD∥MQ，

∴AB∥MQ，

又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ；

C项，作如图③所示的辅助线，则AB∥CD，CD∥MQ，

D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，

∴AB∥NQ，

又AB⊄平面MNQ，NQ⊂平面MNQ，

∴AB∥平面MNQ.

故选A.

6．α，β是两个平面，m，n是两条直线，有下列四个命题：

①如果m⊥n，m⊥α，n∥β，那么α⊥β；

②如果m⊥α，n∥α，那么m⊥n；

③如果α∥β，m⊂α，那么m∥β；

④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．

其中正确的命题有________．（填写所有正确命题的序号）

答案　②③④

解析　当m⊥n，m⊥α，n∥β时，两个平面的位置关系不确定，故①错误，经判断知②③④均正确，故正确答案为②③④.

7．（2018·

贵阳模拟）设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：

①若m⊂α，n∥α，则m∥n；

②若α∥β，β∥γ，m⊥α，则m⊥γ；

③若α∩β＝n，m∥n，m∥α，则m∥β；

④若m∥α，n∥β，m∥n，则α∥β.

其中是真命题的是________．（填序号）

答案　②

解析　①m∥n或m，n异面，故①错误；

易知②正确；

③m∥β或m⊂β，故③错误；

④α∥β或α与β相交，故④错误．

8．棱长为2的正方体ABCD－A1B1C1D1中，M是棱AA1的中点，过C，M，D1作正方体的截面，则截面的面积是________．

答案　

解析　由面面平行的性质知截面与面AB1的交线MN是△AA1B的中位线，所以截面是梯形CD1MN，易求其面积为.

9.如图所示，正方体ABCD－A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度为________．

解析　在正方体ABCD－A1B1C1D1中，AB＝2，

∴AC＝2.

又E为AD中点，EF∥平面AB1C，EF⊂平面ADC，平面ADC∩平面AB1C＝AC，

∴EF∥AC，∴F为DC中点，

∴EF＝AC＝.

10.如图所示，在正四棱柱ABCD—A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M只需满足条件______时，就有MN∥平面B1BDD1.（注：

请填上你认为正确的一个条件即可，不必考虑全部可能情况）

答案　点M在线段FH上（或点M与点H重合）

解析　连接HN，FH，FN，则FH∥DD1，HN∥BD，

∴平面FHN∥平面B1BDD1，只需M∈FH，

则MN⊂平面FHN，∴MN∥平面B1BDD1.

11．（2019·

南昌模拟）如图，在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°

，∠BAC＝∠CAD＝60°

，PA⊥平面ABCD，PA＝2，AB＝1.设M，N分别为PD，AD的中点．

平面CMN∥平面PAB；

（2）求三棱锥P－ABM的体积．

（1）证明　∵M，N分别为PD，AD的中点，∴MN∥PA，

又MN⊄平面PAB，PA⊂平面PAB，

∴MN∥平面PAB.

在Rt△ACD中，∠CAD＝60°

，CN＝AN，

∴∠ACN＝60°

.

又∠BAC＝60°

，∴CN∥AB.

∵CN⊄平面PAB，AB⊂平面PAB，

∴CN∥平面PAB.

又CN∩MN＝N，CN，MN⊂平面CMN，

∴平面CMN∥平面PAB.

（2）解　由

（1）知，平面CMN∥平面PAB，

∴点M到平面PAB的距离等于点C到平面PAB的距离．

∵AB＝1，∠ABC＝90°

，∠BAC＝60°

，∴BC＝，

∴三棱锥P－ABM的体积V＝VM－PAB＝VC－PAB＝VP－ABC＝×

2＝.

12.如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形．

平面A1BD∥平面CD1B1；

（2）若平面ABCD∩平面B1D1C＝直线l，证明：

B1D1∥l.

证明　

（1）由题设知BB1∥DD1且BB1＝DD1，

所以四边形BB1D1D是平行四边形，

所以BD∥B1D1.

又BD⊄平面CD1B1，B1D1⊂平面CD1B1，

所以BD∥平面CD1B1.

因为A1D1∥B1C1∥BC且A1D1＝B1C1＝BC，

所以四边形A1BCD1是平行四边形，

所以A1B∥D1C.

又A1B⊄平面CD1B1，D1C⊂平面CD1B1，

所以A1B∥平面CD1B1.

又因为BD∩A1B＝B，BD，A1B⊂平面A1BD，

所以平面A1BD∥平面CD1B1.

（2）由

（1）知平面A1BD∥平面CD1B1，

又平面ABCD∩平面B1D1C＝直线l，

平面ABCD∩平面A1BD＝直线BD，

所以直线l∥直线BD，

在四棱柱ABCD－A1B1C1D1中，四边形BDD1B1为平行四边形，

所以B1D1∥BD，所以B1D1∥l.

13.如图，正方体ABCD－A1B1C1D1的棱长为1，E，F是线段B1D1上的两个动点，且EF＝，则下列结论中错误的是（　　）

A．AC⊥BF

B．三棱锥A－BEF的体积为定值

C．EF∥平面ABCD

D．异面直线AE，BF所成的角为定值

解析　∵ABCD－A1B1C1D1为正方体，

易证AC⊥平面BDD1B1，

∵BF⊂平面BDD1B1，

∴AC⊥BF