完整版完全平方公式的几何背景专题训练试题精选附答案Word文件下载.docx

完整版完全平方公式的几何背景专题训练试题精选附答案Word文件下载.docx

《完整版完全平方公式的几何背景专题训练试题精选附答案Word文件下载.docx》由会员分享，可在线阅读，更多相关《完整版完全平方公式的几何背景专题训练试题精选附答案Word文件下载.docx（35页珍藏版）》请在冰豆网上搜索。

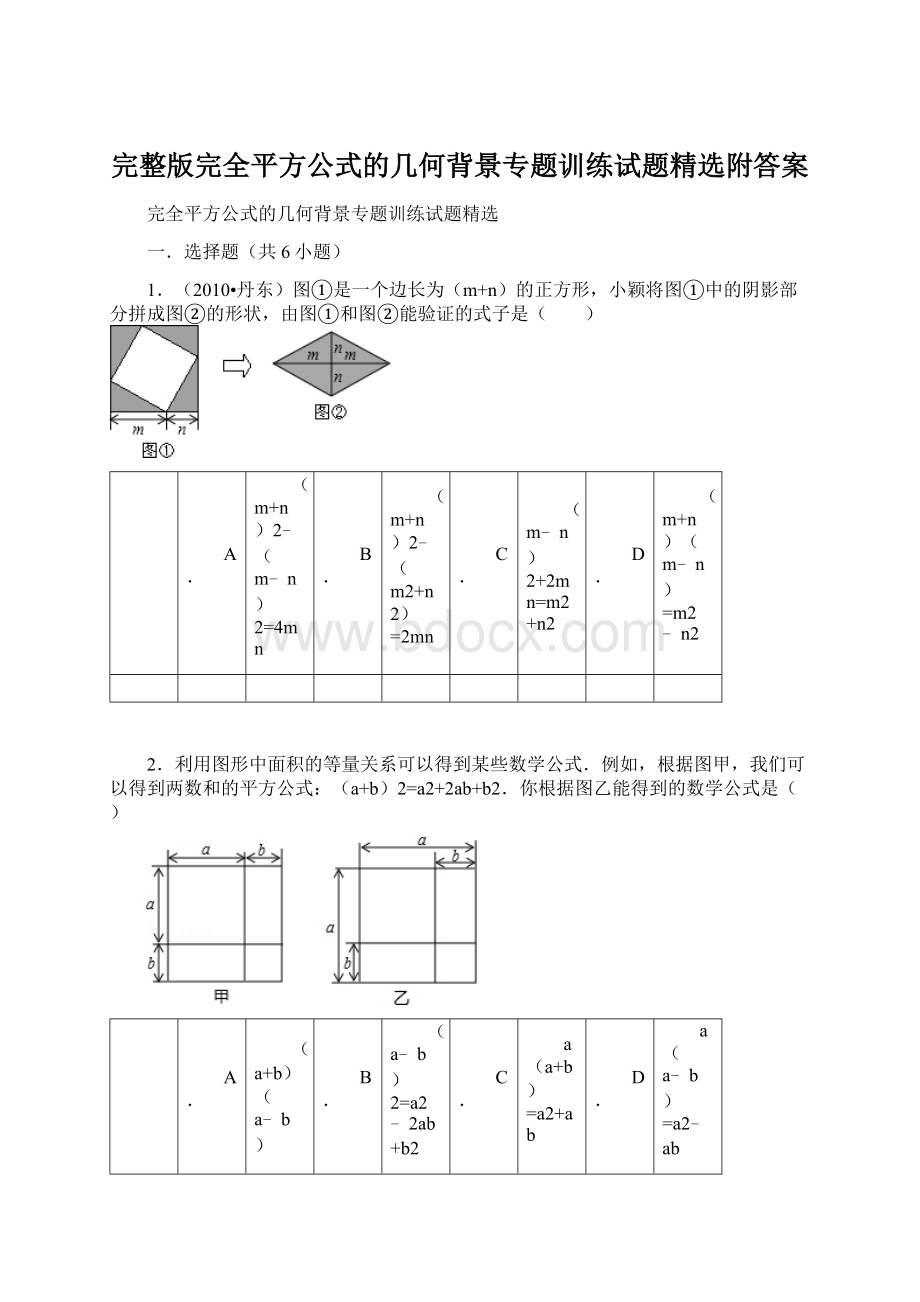
（a+b）2

（a﹣b）2

a2﹣b2

5．如图的图形面积由以下哪个公式表示（　　）

a2﹣b2=a（a﹣b）+b（a﹣b）

6．如果关于x的二次三项式x2﹣mx+16是一个完全平方式，那么m的值是（　　）

8或﹣8

8

﹣8

无法确定

二．填空题（共7小题）

7．（2014•玄武区二模）如图，在一个矩形中，有两个面积分别为a2、b2（a＞0，b＞0）的正方形．这个矩形的面积为　_________　（用含a、b的代数式表示）

8．如图，边长为（m+2）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为2，则另一边长是　_________　．（用含m的代数式表示）

9．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为　_________　．

10．如图1和图2，有多个长方形和正方形的卡片，图1是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．根据图2，利用面积的不同表示方法，写出一个代数恒等式　_________　．

11．如图，正方形广场的边长为a米，中央有一个正方形的水池，水池四周有一条宽度为

的环形小路，那么水池的面积用含a、b的代数式可表示为　_________　平方米．

12．如图，请写出三个代数式（a+b）2、（a﹣b）2、ab之间的等量关系是　_________　．

13．如图，长为a，宽为b的四个小长方形拼成一个大正方形，且大正方形的面积为64，中间小正方形的面积为16，则a=　_________　，b=　_________　．

三．解答题（共10小题）

14．阅读学习：

数学中有很多等式可以用图形的面积来表示．如图1，它表示（m+2n）（m+n）=m2+3mn+2n2，

（1）观察图2，请你写出（a+b）2，（a﹣b）2，ab之间的关系　_________　．

（2）小明用8个一样大的长方形，（长为a，宽为b），拼成了如图甲乙两种图案，图案甲是一个正方形，图案甲中间留下了一个边长为2的正方形；

图形乙是一个长方形．

①a2﹣4ab+4b2=　_________　②ab=　_________　．

15．【学习回顾】我们已经知道，根据几何图形的面积关系可以说明完全平方公式，说明如下：

如图1，正方形ABCD的面积=正方形EBNH的面积+（长方形AEHM的面积+长方形HNCF的面积）+正方形MHFD的面积．即：

（a+b）2=a2+2ab+b2．

【思考问题】还有一些等式也可以用上述方式加以说明，请你尝试完成．

如图2，长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣　_________　的面积，即：

（2a﹣b）（a+b）=　_________　．

【尝试实践】计算（2a+b）（a+b）=　_________　．仿照上述方法，画图并说明．

16．阅读下列文字，我们知道对于一个图形，通过不同的方法计算图形的面积，可以得到一个数学等式，例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2．请解答下列问题：

（1）写出图2中所表示的数学等式　_________　；

（2）利用

（1）中所得到的结论，解决下面的问题：

已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；

（3）图3中给出了若干个边长为a和边长为b的小正方形纸片．若干个长为a和宽为b的长方形纸片，利用所给的纸片拼出一个几何图形，使得计算它的面积能得到数学公式：

2a2+5ab+2b2=（2a+b）（a+2b）．

17．如图1，将一个长为4a，宽为2b的长方形，沿图中虚线均匀分成4个小长方形，然后按图2形状拼成一个正方形．

（1）图2的空白部分的边长是多少？

（用含ab的式子表示）

（2）若2a+b=7，且ab=3，求图2中的空白正方形的面积．

（3）观察图2，用等式表示出（2a﹣b）2，ab和（2a+b）2的数量关系．

18．动手操作：

如图①是一个长为2a，宽为2b的长方形，沿图中的虚线剪开分成四个大小相等的长方形，然后按照图②所示拼成一个正方形．

提出问题：

（1）观察图②，请用两种不同的方法表示阴影部分的面积；

（2）请写出三个代数式（a+b）2，（a﹣b）2，ab之间的一个等量关系．

问题解决：

根据上述

（2）中得到的等量关系，解决下列问题：

已知：

x+y=6，xy=3．求：

（x﹣y）2的值．

19．图①是一个长为2a，宽为2b的长方形，沿图中虚线剪开，可分成四块小长方形．

（1）将图①中所得的四块长为a，宽为b的小长方形拼成一个正方形（如图②）．请利用图②中阴影部分面积的不同表示方法，直接写出代数式（a+b）2、（a﹣b）2、ab之间的等量关系是　_________　；

（2）根据

（2）题中的等量关系，解决如下问题：

已知m+n=8，mn=7，则m﹣n=　_________　；

（3）将如图①所得的四块长为a，宽为b的小长方形不重叠地放在长方形ABCD的内部（如图③），未被覆盖的部分（两个长方形）用阴影表示．若左下角与右上角的阴影部分的周长之差为4，且小长方形的周长为8，则每一个小长方形的面积为　_________　．

20．把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的式子，或可以求出一些不规则图形的面积．

（1）如图1，是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的方法计算这个图形的面积，你能发现什么结论，请写出来．

（2）如图2，是将两个边长分别为a和b的正方形拼在一起，B、C、G三点在同一直线上，连接BD和BF，若两正方形的边长满足a+b=10，ab=20，你能求出阴影部分的面积吗？

21．阅读材料并填空：

我们知道，完全平方式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式样也可以用这种形式表示，

如：

（2a+b）（a+b）=2a2+3ab+b2，就可以用图

（1），或图

（2）等图形的面积表示．

请你写出图（3）所表示的代数恒等式　_________　．

请你写出图（4）所表示的代数恒等式　_________　．

22．图1是一个长为2x、宽为2y的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．

（1）你认为图2中的阴影部分的正方形的边长等于　_________　．

（2）试用两种不同的方法求图2中阴影部分的面积．

方法1：

　_________　；

方法2：

　_________　．

（3）根据图2你能写出下列三个代数式之间的等量关系吗？

代数式：

（x+y）2，（x﹣y）2，4xy．　_________　

（4）根据（3）题中的等量关系，解决如下问题：

若x+y=4，xy=3，则（x﹣y）2=　_________　．

23．已知图甲是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均匀分成四小块长方形，然后按图乙的形状拼成一个正方形．

（1）你认为图乙中阴影部分的正方形的边长等于多少？

（2）请用两种不同的方法求图乙中阴影部分的面积．

方法一：

方法二：

（3）观察图乙，你能写出下列三个代数式之间的等量关系吗？

（m+n）2；

（m﹣n）2；

mm

若a+b=8，ab=5，求（a﹣b）2的值．

参考答案与试题解析

考点：

完全平方公式的几何背景．菁优网版权所有

专题：

计算题；

压轴题．

分析：

根据图示可知，阴影部分的面积是边长为m+n的正方形减去中间白色的正方形的面积m2+n2，即为对角线分别是2m，2n的菱形的面积．据此即可解答．

解答：

解：

（m+n）2﹣（m2+n2）=2mn．

故选B．

点评：

本题是利用几何图形的面积来验证（m+n）2﹣（m2+n2）=2mn，解题关键是利用图形的面积之间的相等关系列等式．

根据图形，左上角正方形的面积等于大正方形的面积减去两个矩形的面积，然后加上多减去的右下角的小正方形的面积．

大正方形的面积=（a﹣b）2，

还可以表示为a2﹣2ab+b2，

∴（a﹣b）2=a2﹣2ab+b2．

正确列出正方形面积的两种表示是得出公式的关键，也考查了对完全平方公式的理解能力．

根据图形得出阴影部分的面积是（a﹣b）2和b2，剩余的矩形面积是（a﹣b）b和（a﹣b）b，即大阴影部分的面积是（a﹣b）2，即可得出选项．

从图中可知：

阴影部分的面积是（a﹣b）2和b2，剩余的矩形面积是（a﹣b）b和（a﹣b）b，

即大阴影部分的面积是（a﹣b）2，

∴（a﹣b）2=a2﹣2ab+b2，

故选C．

本题考查了完全平方公式的应用，主要考查学生的阅读能力和转化能力，题目比较好，有一定的难度．

先求出正方形的边长，继而得出面积，然后根据空白部分的面积=正方形的面积﹣矩形的面积即可得出答案．

由题意可得，正方形的边长为（a+b），

故正方形的面积为（a+b）2，

又∵原矩形的面积为4ab，

∴中间空的部分的面积=（a+b）2﹣4ab=（a﹣b）2．

此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的关键，难度一般．

通过图中几个图形的面积的关系来进行推导．

根据图形可得出：

大正方形面积为：

（a+b）2，大正方形面积=4个小图形的面积和=a2+b2+ab+ab，

∴可以得到公式：

故选：

本题考查了完全平方公式的推导过程，运用图形的面积表示是解题的关键．

根据两平方项确定出这两个数，再根据乘积二倍项列式求解即可．

∵x2﹣mx+16是一个完全平方式，

∴﹣mx=±

2×

4•x，

解得m=±

8．

故选A．

本题是完全平方公式的考查，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．

7．（2014•玄武区二模）如图，在一个矩形中，有两个面积分别为a2、b2（a＞0，b＞0）的正方形．这个矩形的面积为　（a+b）2　（用含a、b的代数式表示）

求出大正方形的边长为a+b，再利用正方形的面积公式求解．

解；

∵两个小矩形的长为a，宽为b，

∴正方形的边长为：

a+b

∴它的面积为：

故答案为：

本题主要考查完全平方公式的几何表示，运用不同方法表示阴影部分面积是解题的关键．

8．如图，边长为（m+2）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为2，则另一边长是　2m+2　．（用含m的代数式表示）

几何图形问题．

由于边长为（m+2）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），那么根据正方形的面积公式，可以求出剩余部分的面积，而矩形一边长为2，利用矩形的面积公式即可求出另一边长．

依题意得剩余部分为

（m+2）2﹣m2=m2+4m+4﹣m2=4m+4，

而拼成的矩形一边长为2，

∴另一边长是（4m+4）÷

2=2m+2．

2m+2．

本题主要考查了多项式除以单项式，解题关键是熟悉除法法则．

9．有两个正方形A，B，现将B放在A的内部得图甲，将A，B并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为1和12，则正方形A，B的面积之和为　13　．

设正方形A的边长为a，正方形B的边长为b，由图形得出关系式求解即可．

设正方形A的边长为a，正方形B的边长为b，

由图甲得a2﹣b2﹣2（a﹣b）=1即a2+b2﹣2ab=1，

由图乙得（a+b）2﹣a2﹣b2=12，2ab=12，

所以a2+b2=13，

13．

本题主要考查了完全平方公式的几何背景，解题的关键是根据图形得出数量关系．

10．如图1和图2，有多个长方形和正方形的卡片，图1是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证等式a（a+b）=a2+ab成立．根据图2，利用面积的不同表示方法，写出一个代数恒等式　（a+b）（a+2b）=a2+2b2+3ab　．

计算题．

表示阴影部分的面积有两种方法：

①大长方形的面积=（a+b）（a+2b），②3个正方形的面积加上3个矩形的面积a2+ab+ab+ab+b2+b2，推出即可．

由图2可知：

阴影部分的面积是：

①（a+b）（a+2b），②a2+ab+ab+ab+b2+b2=a2+2b2+3ab，

∴（a+b）（a+2b）=a2+2b2+3ab，

（a+b）（a+2b）=a2+2b2+3ab．

本题考查了完全平方公式的几何背景的应用，关键是检查学生能否正确表示图形中阴影部分的面积，题目具有一定的代表性，考查了学生的理解能力、观察图形的能力等

的环形小路，那么水池的面积用含a、b的代数式可表示为　a2﹣4ab+4b2或（a﹣2b）2　平方米．

根据图示计算出中央正方形的水池的边长，然后根据正方形的面积公式来计算水池的面积．

水池的边长是：

a﹣2b，

所以，正方形水池的面积是（a﹣2b）（a﹣2b）=a2﹣4ab+4b2或（a﹣2b）（a﹣2b）=（a﹣2b）2．

故答案是：

a2﹣4ab+4b2或（a﹣2b）2．

本题考查对完全平方公式几何意义的理解．解题时，主要围绕图形面积展开分析．

12．如图，请写出三个代数式（a+b）2、（a﹣b）2、ab之间的等量关系是　a+b）2=（a﹣b）2+4ab　．

通过观察图形知：

（a+b）2，（a﹣b）2，ab分别表示的是大正方形、空白部分的正方形及小长方形的面积．

由图可以看出，大正方形面积=阴影部分的正方形的面积+四个小长方形的面积，

即：

（a+b）2=（a﹣b）2+4ab，

（a+b）2=（a﹣b）2+4ab．

此题考查了学生观察、分析图形解答问题的综合能力，关键是通过观察图形找出各图形之间的关系．

13．如图，长为a，宽为b的四个小长方形拼成一个大正方形，且大正方形的面积为64，中间小正方形的面积为16，则a=　6　，b=　2　．

先求出大正方形的边长为：

a+b，小正方形的边长为：

a﹣b，再列出方程组求解．

大正方形的边长为：

a﹣b

解得

6，2．

本题的关键是求出大正方形的边长和小正方形的边长．列出方程组．

（1）观察图2，请你写出（a+b）2，（a﹣b）2，ab之间的关系　（a+b）2﹣（a﹣b）2=4ab　．

①a2﹣4ab+4b2=　4　②ab=　60　．

数形结合．

根据图形的面积公式来进行分析即可得到．

（1）（a+b）2﹣（a﹣b）2=4ab；

（2）①4②ab=60

该题目考查了利用图形的面积来得到数学公式，关键是灵活进行数学结合来分析．

如图2，长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣　正方形MHFD　的面积，即：

（2a﹣b）（a+b）=　2a2﹣ab﹣b2　．

【尝试实践】计算（2a+b）（a+b）=　2a2+3ab+b2　．仿照上述方法，画图并说明．

（1）利用长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积计算．

（2）利用长方形ABCD的面积=正方形GBHF的面积+正方形FHQN的面积+长方形AGFE的面积+长方形EFNM的面积+长方形NQCO的面积+正方形MNOD的面积计算．

（1）长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积，即：

（2a﹣b）（a+b）=2a2﹣ab﹣b2．

正方形MHFD，2a2﹣ab﹣b2．

（2）（2a+b）（a+b）=2a2+3ab+b2．

如图，

2a2﹣ab﹣b2．

本题主要考查了完全平方公式的几何背景，解题的关键是通过几何图形之间的数量关系对公式做出几何解释．

（1）写出图2中所表示的数学等式　（a+b+c）2=a2+b2+c2+2ab+2ac+2bc　；

已知