1819 第2章 1交变电流Word文件下载.docx

1819 第2章 1交变电流Word文件下载.docx

《1819 第2章 1交变电流Word文件下载.docx》由会员分享，可在线阅读，更多相关《1819 第2章 1交变电流Word文件下载.docx（12页珍藏版）》请在冰豆网上搜索。

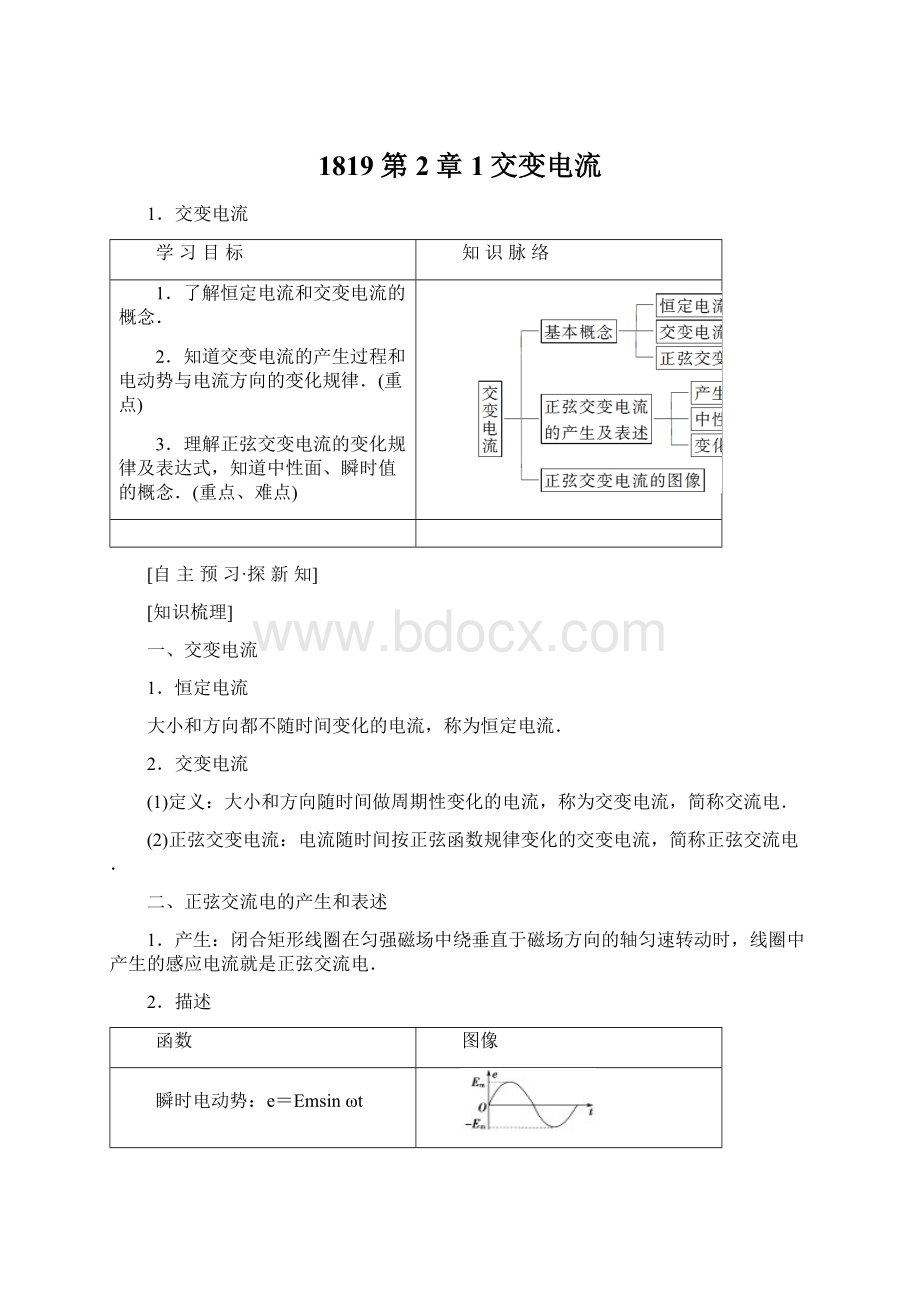
瞬时电压：

u＝Umsin_ωt

瞬时电流：

i＝Imsin_ωt

最大值表达式：

Em＝NBSω.

3．中性面：

线圈平面与磁场垂直的位置．

[基础自测]

1．思考判断

（1）交变电流指的是正弦交流电．（×

）

（2）教室的照明电路中所用的是正弦式交流电．（√）

（3）电流方向做周期性变化的电流就是交变电流．（√）

（4）只要闭合线圈在匀强磁场里匀速转动就一定产生正弦交变电流．（×

（5）正弦交变电流的函数形式与计时起点有关．（√）

（6）当线圈中的磁通量为零时，产生的电流也为零．（×

2．下列四个图像中不属于交流电的是（　　）

D　[A、B、C中e的方向均做周期性变化，故它们属于交流电，D中e的大小变化而方向不变，属直流电．]

3．如图211所示，一线圈在匀强磁场中匀速转动，经过图示位置时（　　）

【导学号：

24622053】

图211

A．穿过线圈的磁通量最小，磁通量的变化率最大

B．穿过线圈的磁通量最大，磁通量的变化率最大

C．穿过线圈的磁通量最大，磁通量的变化率最小

D．穿过线圈的磁通量最小，磁通量的变化率最小

A　[由图可知线圈平面与磁感线平行，应处于垂直于中性面的平面，此时穿过线圈的磁通量最小，磁通量的变化率最大，所以A选项正确．]

[合作探究·

攻重难]

交变电流的产生

1．产生

在匀强磁场中，绕垂直磁场方向的轴匀速转动的线圈中产生的是交变电流，实验装置如图212所示．

图212

2．过程分析（如图213所示）

图213

线圈由甲位置转到乙位置过程中，电流方向为b→a→d→c.

线圈由乙位置转到丙位置过程中，电流方向为b→a→d→c.

线圈由丙位置转到丁位置过程中，电流方向为a→b→c→d.

线圈由丁位置转到甲位置过程中，电流方向为a→b→c→d.

3．两个特殊位置对比

位置

中性面

中性面的垂面

磁通量

最大

零

磁通量变化率

感应电动势

线圈边缘切割磁感线的有效速度

感应电流

电流方向

改变

不变

　（多选）矩形线框绕垂直于匀强磁场且在线框平面内的轴匀速转动时产生了交变电流，下列说法正确的是（　　）

24622054】

A．当线框位于中性面时，线框中感应电动势最大

B．当穿过线框的磁通量为零时，线框中的感应电动势也为零

C．每当线框经过中性面时，感应电动势或感应电流的方向就改变一次

D．线框经过中性面时，各边切割磁感线的速度为零

CD　[线框位于中性面时，线框平面与磁感线垂直，穿过线框的磁通量最大，原来切割磁感线的两边此时与磁感线平行，即不切割磁感线，所以感应电动势等于零，此时穿过线框的磁通量的变化率也等于零，感应电动势或感应电流的方向也就在此时发生变化．线框垂直于中性面时，穿过线框的磁通量为零，但切割磁感线的两边都垂直切割磁感线，有效切割速度最大，所以感应电动势最大，也可以说此时穿过线框的磁通量的变化率最大，故C、D选项正确．]

[针对训练]

1．（多选）下列各图中，线圈中能产生交变电流的有（　　）

A　　　　　　　　　B

C　　　　　　　　　D

BCD　[B、C、D中当线圈在磁场中转动时，穿过线圈的磁通量变化，会产生感应电流，而A中线圈转动时，穿过线圈的磁通量始终为零，无感应电流产生，故B、C、D正确．]

2．（多选）如图214甲所示，一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的轴OO′以恒定的角速度ω转动．从线圈平面与磁场方向平行时开始计时，线圈中产生的交变电流按照如图214乙所示的余弦规律变化，则在t＝

时刻（　　）

甲　　　　　　　　　　乙

图214

A．线圈中的电流最大

B．穿过线圈的磁通量为零

C．线圈所受的安培力为零

D．线圈中的电流为零

CD　[线圈转动的角速度为ω，则转过一圈用时

，当t＝

时说明转过了

圈，此时线圈位于中性面位置，所以穿过线圈的磁通量最大，B错误；

由于此时感应电动势为零，所以线圈中电流为零，线圈所受的安培力为零，A错误，C、D正确．]

正弦交流电的瞬时值和最大值

1．瞬时值表达式的推导

图215

若线圈平面从中性面开始转动，如图215所示，则经时间t：

纯电阻电路电流的瞬时值：

i＝

＝

sinωt＝Imsinωt

某个电阻R′电压的瞬时值：

u＝iR′＝ImR′sinωt＝Umsinωt

2．峰值表达式

（1）Em＝NBSω＝NΦmω.

（2）Im＝

.

（3）Um＝ImR′.

3．正弦交变电流的瞬时值表达式

（1）e＝NBSωsinωt＝Emsinωt.

（2）i＝

sinωt＝Imsinωt.

（3）u＝iR＝ImRsinωt＝Umsinωt.

上面各式中的e、i、u仅限于从中性面开始计时的情况．若从垂直于中性面（即从线圈平面与磁场平行时）开始计时，则上述表达式应为e＝Emcosωt，i＝Imcosωt，u＝Umcosωt.

　一矩形线圈，面积是0.05m2，共100匝，线圈电阻r＝2Ω，外接电阻R＝8Ω，线圈在磁感应强度B＝

T的匀强磁场中以n＝300r/min的转速绕垂直于磁感线的轴匀速转动，如图216所示，若从中性面开始计时，求：

图216

（1）线圈中感应电动势的瞬时值表达式；

（2）线圈从开始计时经

s时线圈中由此得到的感应电流的瞬时值；

（3）外电路R两端电压瞬时值的表达式．

思路点拨：

①线圈在匀强磁场中绕垂直于磁场的轴匀速转动时电动势的最大值Em＝NBSω.②感应电动势瞬时值表达式与开始计时的位置有关，若从中性面开始计时，则e＝Emsinωt.

【解析】　

（1）线圈转速n＝300r/min＝5r/s

角速度ω＝2πn＝10πrad/s

线圈产生的感应电动势最大值Em＝NBSω＝50V

由此得到的感应电动势瞬时值表达式为

e＝Emsinωt＝50sin10πtV.

（2）将t＝

s代入感应电动势瞬时值表达式中，

得e′＝50sin（10π×

）V＝25

V

对应的感应电流i′＝

A.

（3）由欧姆定律得u＝

R＝40sin10πtV.

【答案】　

（1）e＝50sin10πtV　

（2）

A　

（3）u＝40sin10πtV

（1）求交变电流瞬时值的方法

①确定线圈转动从哪个位置开始计时；

②确定表达式是正弦函数还是余弦函数；

③确定转动的角速度ω＝2πn（n的单位为r/s）、Em＝NBSω；

④写出表达式，代入角速度求瞬时值．

（2）线圈在匀强磁场中匀速转动产生正弦式交变电流，产生的交变电流与线圈的形状无关．如图所示，若线圈的面积与例2中题图所示线圈面积相同，则答案完全相同．

3．某线圈在匀强磁场中转动所产生的电动势变化规律为e＝Emsinωt，保持其他条件不变，使该线圈的转速和匝数同时增加一倍，则此时所产生的电动势的瞬时值表达式为（　　）

24622055】

A．e′＝2Emsin2ωt　　　B．e′＝2Emsinωt

C．e′＝4Emsin2ωtD．e′＝4Emsinωt

C　[因ω＝2πn，故转速加倍时，角速度也加倍，根据Em＝NBSω，转速和匝数均加倍时，电动势的峰值将变为原来的4倍，所以选项C正确．]

4.一矩形线圈在匀强磁场中匀速转动时，产生的感应电动势最大值为50V，那么该线圈从如图217所示位置转过30°

时，线圈中的感应电动势大小为（　　）

图217

A．50VB．25

C．25VD．10V

B　[矩形线圈从图示位置开始计时转动产生的感应电动势e＝50cosωtV，所以当线圈转过30°

时，线圈中的感应电动势大小为50cos30°

V＝25

V，选项B正确．]

交变电流的图像问题

交变电流随时间t的变化规律不再是简单的正比例关系，所以借助图像来分析研究比单纯用代数的方法更简捷、直观．

1．从如图218所示的交变电流定以下量：

图218

（1）可以读出电动势的最大值Em.

（2）可根据线圈转至中性面时电动势为零的特点，确定线圈处于中性面的时刻，确定了该时刻，也就确定了磁通量最大的时刻和磁通量变化率最小的时刻．

（3）可根据线圈转至与磁场平行时感应电动势最大的特点，确定线圈与中性面垂直的时刻，此时刻也就是磁通量为零的时刻和磁通量变化率最大的时刻．

（4）可以确定某一时刻电动势大小以及某一时刻电动势的变化趋势．

2．交变电流的电压或电流变化的快慢（变化率），在图线上等于某瞬间切线的斜率，它与电压或电流瞬时值的大小是两回事．瞬时值最大时，变化率最小（等于零）；

瞬时值为零时，变化率恰好最大．在具体问题中，必须弄清楚哪些量与瞬时值有关，哪些量与变化率有关．

　（多选）一矩形线圈，绕垂直于匀强磁场并位于线圈平面内的固定轴匀速转动．线圈中的感应电动势e随时间t变化的规律如图219所示，则下列说法正确的是（　　）

图219

A．图中是从线圈平面与磁场方向平行时开始计时的

B．t1和t3时刻穿过线圈的磁通量为零

C．t1和t3时刻穿过线圈的磁通量的变化率为零

D．感应电动势e的方向变化时，穿过线圈的磁通量最大

解答本题时应弄清以下两点：

①线圈转动过程中几个特殊位置的特点．②磁通量、磁通量的变化率、感应电动势、感应电流之间的关系．

ACD　[由题图可知，当t＝0时，感应电动势最大，说明穿过线圈的磁通量的变化率最大，磁通量为零，即是从线圈平面与磁场方向平行时开始计时的，选项A正确；

t1、t3时刻感应电动势为零，穿过线圈的磁通量的变化率为零，磁通量最大，选项B错误，C正确；

感应电动势e的方向变化时，线圈通过中性面，穿过线圈的磁通量最大，选项D正确．]

交变电流图像问题的分析方法

（1）看清两轴物理量的物理意义，分清是何种图像．

（2）分析“斜率”“截距”“点”表示的物理意义．

（3）掌握“图与图”“图与式”和“图与物”间的对应关系．

5.（多选）一矩形线圈的匝数为50匝，在匀强磁场中绕垂直于磁场方向的轴匀速转动时，穿过线圈的磁通量随时间的变化规律如图2110所示．下列结论正确的是（　　）

图2110

A．在t＝0.1s和t＝0.3s时，电动势最大

B．在t＝0.2s和t＝0.4s时，电动势方向发生改变

C．电动势的最大值是157V

D．在t＝0.4s时，磁通量的变化率最大，为3.14Wb/s

CD　[在t＝0.1s和t＝0.3s时，穿过线圈的磁通量最大，但其变化率为零，电动势为零，选项A错误；

在t＝0.2s和t＝0.4s时，穿过线圈的磁通量为零，但磁通量的变化率最大，电动势最大，电动势方向不变，选项B错误；

根据电动势的最大值Em＝nBSω，Φm＝BS，ω＝

，可得Em＝50×

0.2×

V＝157V，选项C正确；

在t＝0.4s时，磁通量的变化率最大，为

＝3.14Wb/s，选项D正确．]

6．如图2111甲所示，一矩形线圈abcd放置在匀强磁场中，并绕过ab、cd中点的轴OO′以角速度ω逆时针匀速转动．若以线圈平面与磁场夹角θ＝45°

时（如图2111乙）为计时起点，并规定当电流自a流向b时电流方向为正．下列四个选项中正确的是（　　）

图2111

B　[当从题图乙所示位置转过

时刻，线圈处在中性面位置，感应电流为零，且在此段转动时间内电流方向为从b流向a，故选项B正确．]

[当堂达标·

固双基]

1．（多选）关于交变电流和直流电的说法中，正确的是（　　）

24622056】

A．如果电流大小做周期性变化，则一定是交变电流

B．直流电的大小可以变化，但方向一定不变

C．交变电流一定是按正弦或余弦规律变化的

D．交变电流的最大特征就是电流的方向发生周期性的变化

BD　[直流电的特征是电流方向不变，交流电的特征是电流方向周期性改变．另外交变电流不一定都是正弦交流电或余弦交流电．故选B、D.]

2．（多选）矩形线圈在匀强磁场中绕垂直磁场的轴匀速转动，在线圈平面经过中性面瞬间（　　）

A．线圈平面与磁感线平行

B．通过线圈的磁通量最大

C．线圈中的感应电动势最大

D．线圈中感应电流的方向改变

BD　[在线圈平面垂直于磁感线时，各边都不切割磁感线，线圈中没有感应电流，这样的位置叫做中性面．根据这一定义，线圈平面经过中性面瞬间，通过线圈的磁通量最大，线圈中的感应电动势为零，此时，感应电流的方向发生改变，所以选项B、D正确．]

3．如图2112所示为演示交变电流产生的装置图，关于这个实验，正确的说法是（　　）

24622057】

图2112

A．线圈每转动一周，指针左右摆动两次

B．图示位置为中性面，线圈中无感应电流

C．图示位置ab边的感应电流方向为a→b

D．线圈平面与磁场方向平行时，磁通量变化率为零

C　[线圈在磁场中匀速转动时，在电路中产生呈周期性变化的交变电流，图示位置为垂直中性面，线圈中感应电流最大，故B错误；

线圈经过中性面时电流改变方向，线圈每转动一周，有两次通过中性面，电流方向改变两次，指针左右摆动一次；

线圈处于图示位置时，ab边向右运动，由右手定则知，ab边的感应电流方向为a→b；

线圈平面与磁场方向平行时，ab、cd边垂直切割磁感线，线圈产生的电动势最大，也可以这样认为，线圈处于竖直位置时，磁通量为零，但磁通量的变化率最大．]

4．有一10匝正方形线框，边长为20cm，线框总电阻为1Ω，线框绕OO′轴以10πrad/s的角速度匀速转动，如图2113，垂直于线框平面向里的匀强磁场的磁感应强度为0.5T．问：

图2113

（1）该线框产生的交变电流电动势最大值、电流最大值分别是多少？

（2）线框从图示位置转过60°

时，感应电动势的瞬时值是多大？

（3）写出感应电动势随时间变化的表达式．

【解析】　

（1）交变电流电动势最大值为Em＝NBSω＝10×

0.5×

0.22×

10πV＝6.28V

电流的最大值为Im＝

A＝6.28A.

（2）线框转过60°

时，感应电动势

E＝Emsin60°

＝5.44V.

（3）由于线框转动是从中性面开始计时的，所以瞬时值表达式为e＝Emsinωt＝6.28sin10πtV.

【答案】　

（1）6.28V　6.28A　

（2）5.44V

（3）e＝6.28sin10πtV