北师大版初二数学下册《第3章达标检测卷》附答案Word文档下载推荐.docx
《北师大版初二数学下册《第3章达标检测卷》附答案Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《北师大版初二数学下册《第3章达标检测卷》附答案Word文档下载推荐.docx(10页珍藏版)》请在冰豆网上搜索。
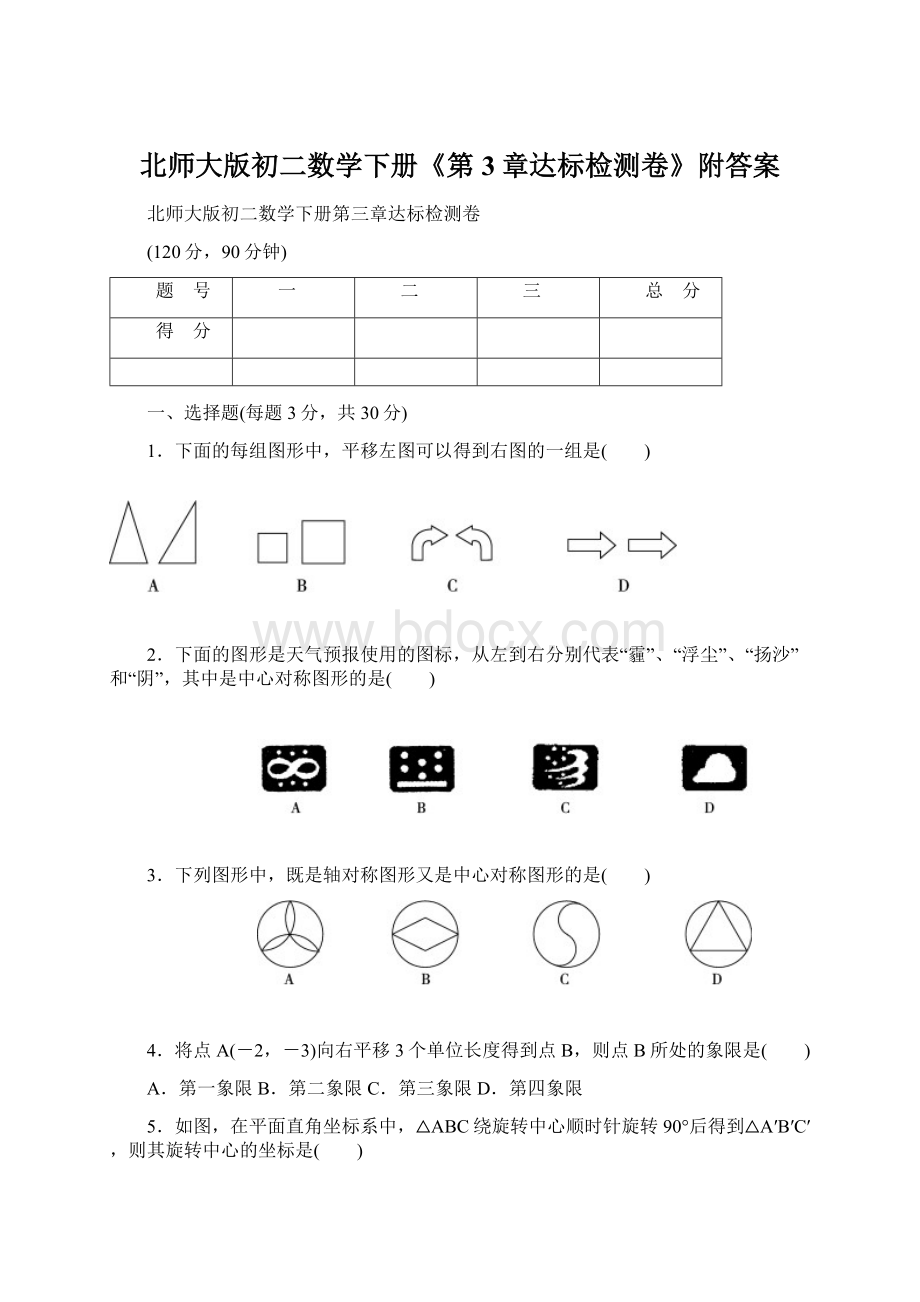
6.如图,在Rt△ABO中,∠ABO=90°
,OA=2,AB=1,把Rt△ABO绕着原点逆时针旋转90°
,得△A′B′O,那么点A′的坐标为( )
A.(-
,1)B.(-2,
)C.(-1,
)D.(-
,2)
(第5题)
(第6题)
(第8题)
7.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.在成中心对称的两个图形中,连接对称点的线段都被对称中心平分
C.在平面直角坐标系中,一点向右平移a个单位长度,则该点的纵坐标加a
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
8.如图,在正方形ABCD中,点E为DC边上的点,连接BE,若△BCE绕C点按顺时针方向旋转90°
得到△DCF,连接EF,若∠BEC=60°
,则∠EFD的度数为( )
A.10°
B.15°
C.20°
D.25°
9.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°
,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC平移的距离为( )
A.4B.5C.6D.8
(第9题)
(第10题)
10.如图,在Rt△ABC中,∠ACB=90°
,∠B=30°
,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;
将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
;
将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
…,按此规律继续旋转,得到点P2018为止,则AP2018等于( )
A.2016+673
B.2017+673
C.2018+673
D.2019+673
二、填空题(每题3分,共24分)
11.如图,已知△ABD沿BD方向平移到了△FCE的位置,若BE=12,CD=5,则平移的距离是________.
12.在平面直角坐标系中,将点P(-2,1)先向右平移3个单位长度,再向上平移4个单位长度,得到点P′,则点P′的坐标是________.
13.在平面直角坐标系中,点(a,5)关于原点对称的点的坐标是(1,b+1),则a+b的值为________.
14.等边三角形至少绕中心旋转________才能与自身重合.
15.如图,△ABC的顶点分别为A(3,6),B(1,3),C(4,2).若将△ABC绕点B顺时针旋转90°
,得到△A′BC′,则点A的对应点A′的坐标为________.
(第11题)
(第15题)
(第16题)
(第17题)
16.如图,把边长为3cm的正方形ABCD先向右平移1cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为________.
17.如图,在△AOB中,AO=AB,点A的坐标是(4,4),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上,点O′,B′在x轴上,则点O′的坐标是________.
(第18题)
18.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°
,将△ADC绕点A顺时针旋转90°
后得到△AFB,连接EF,则有下列结论:
①△AED≌△AEF;
②BE+DC=DE;
③S△ABE+S△ACD>S△AED;
④BE2+DC2=DE2.其中正确的是________(填入所有正确结论的序号).
三、解答题(19~21题每题10分,22~24题每题12分,共66分)
19.如图,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°
,得到△A1B2C2,在网格中画出旋转后的△A1B2C2.
(第19题)
20.如图所示,在Rt△ABC中,∠ACB=90°
,AC=4cm,BC=3cm,△ABC沿AB方向平移至△DEF,若AE=8cm,BD=2cm.求:
(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
(第20题)
21.如图所示,△ABO与△CDO关于O点中心对称,点E,F在线段AC上,且AF=CE.求证:
FD=EB.
(第21题)
22.实践与操作:
现有如图①所示的两种瓷砖,请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案,使拼铺的图案是轴对称图形或中心对称图形(如图②所示).
(1)分别在图③、图④中各设计一种与图②不同的拼法,使其中的一个是轴对称图形而不是中心对称图形,另一个是中心对称图形而不是轴对称图形;
(2)分别在图⑤、图⑥中各设计一个拼铺图案,使这两个图案都既是轴对称图形又是中心对称图形,且互不相同(两个图案之间若能通过轴对称、平移、旋转变换相互得到,则视为相同图案).
(第22题)
23.如图①所示,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF,BE.
(1)线段AF和BE有怎样的数量关系?
请说明理由.
(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,
(1)中的结论还成立吗?
作出判断并说明理由.
(第23题)
24.在平面直角坐标系xOy中,如图,已知Rt△DOE中,∠DOE=90°
,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5,∠ACB+∠ODE=180°
,∠B=∠OED,BC=DE.
(1)将△ODE绕O点按逆时针方向旋转90°
得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN(不写作法,保留作图痕迹);
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与
(1)中的△OMN的边NM的重合,画出△A′B′C′(不写作法,保留作图痕迹);
(3)求OE的长.
(第24题)
参考答案及解析
一、1.D 2.A 3.B 4.D 5.C
6.C 点拨:
在Rt△ABO中,∠ABO=90°
,OA=2,AB=1,所以OB′=OB=
,A′B′=AB=1.因为点A′在第二象限,所以点A′的坐标为(-1,
).故选C.
7.B 8.B
9.A 点拨:
∵点A,B的坐标分别为(1,0),(4,0),∴AB=3.又∵∠CAB=90°
,BC=5,∴AC=4.当点C落在直线y=2x-6上时,令2x-6=4,解得x=5,故线段BC平移的距离为5-1=4.
10.C 点拨:
∵在Rt△ABC中,∠ACB=90°
,AC=1,∴AB=2.∴BC=
.由题意知,AP1=2,AP2=2+
,AP3=2+
+1=3+
,每三次旋转为一个循环,又∵2018÷
3=672……2,∴AP2018=672(3+
)+2+
=2018+673
.故选C.
二、11.3.5 12.(1,5) 13.-7
14.120°
15.(4,1) 16.4cm2
17.(-4,0)
18.①③④ 点拨:
由旋转的性质知AF=AD,BF=CD,∠FBA=∠DCA,∠FAD=∠BAC=90°
,∴∠FAE=∠EAD=45°
.又AE=AE,∴△AED≌△AEF.∴DE=EF.∵∠EBF=∠FBA+∠ABE=∠ACD+∠ABE=90°
,∴BE2+BF2=BE2+DC2=EF2=DE2.S△ABE+S△ACD=S△ABE+S△AFB>S△AED,BE+DC=BE+FB>EF=ED,∴正确的结论是①③④.
三、19.解:
(1)如图.
(2)如图.
20.解:
(1)∵△ABC沿AB方向平移至△DEF,
∴AD=BE.
∵AE=8cm,BD=2cm,
∴AD=
=3(cm),
即△ABC沿AB方向平移的距离是3cm.
(2)由平移的特征及
(1)得,
CF=AD=3cm,EF=BC=3cm.
又AE=8cm,AC=4cm,
∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
21.证明:
∵△ABO与△CDO关于O点中心对称,
∴OB=OD,OA=OC.
∵AF=CE,
∴OF=OE.
在△DOF和△BOE中,OD=OB,∠DOF=∠BOE,OF=OE,
∴△DOF≌△BOE(SAS).
∴FD=EB.
22.解:
(1)如图①是轴对称图形而不是中心对称图形.
如图②是中心对称图形而不是轴对称图形.
(2)如图③、图④、图⑤既是轴对称图形又是中心对称图形(画出其中的两个即可).
点拨:
本题答案不唯一.
23.解:
(1)AF=BE.
理由如下:
∵△ABC和△CEF是等边三角形,∴AC=BC,CF=CE,∠ACF=∠BCE=60°
.
在△AFC与△BEC中,
∴△AFC≌△BEC(SAS).
∴AF=BE.
(2)成立.
理由:
∵△ABC和△CEF是等边三角形,
∴AC=BC,CF=CE,∠ACB=∠FCE=60°
∴∠ACB-∠FCB=∠FCE-∠FCB,即∠ACF=∠BCE.
24.解:
(1)△OMN如图所示.
(2)△A′B′C′如图所示.
(3)设OE=x,则ON=x,过点M作MF⊥A′B′于点F,如图所示.由作图可知,
∠ONC′=∠OED,∠A′B′C′=∠B,
∵∠B=∠OED,
∴∠ONC′=∠A′B′C′.
∴B′C′平分∠A′B′O.
∵C′O⊥OB′,
易得△FB′C′≌△OB′C′.
∴B′F=B′O=OE=x,FC′=OC′=OD=3.
∵A′C′=AC=5,
∴A′F=
=
=4,
∴A′B′=x+4,A′O=5+3=8.
在Rt△A′B′O中,A′O2+NO2=A′B′2,即82+x2=(4+x)2,解得x=6.∴OE=6.