新人教版八年级数学《三角形》重点难点培优训练习试题集Word文档格式.docx

新人教版八年级数学《三角形》重点难点培优训练习试题集Word文档格式.docx

《新人教版八年级数学《三角形》重点难点培优训练习试题集Word文档格式.docx》由会员分享，可在线阅读，更多相关《新人教版八年级数学《三角形》重点难点培优训练习试题集Word文档格式.docx（5页珍藏版）》请在冰豆网上搜索。

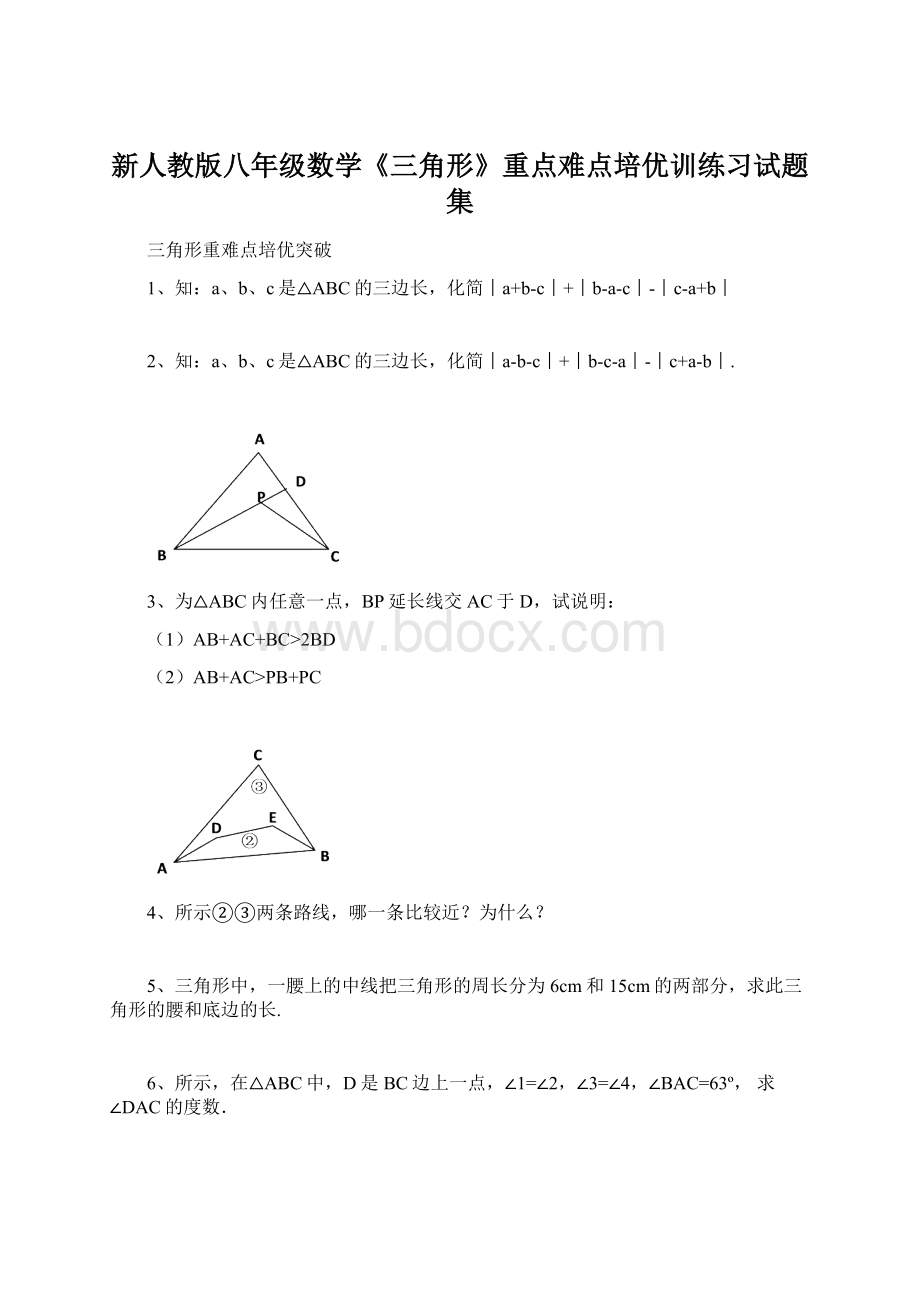
3、为△ABC内任意一点，BP延长线交AC于D，试说明：

（1）AB+AC+BC>

2BD

（2）AB+AC>

PB+PC

4、所示②③两条路线，哪一条比较近？

为什么？

5、三角形中，一腰上的中线把三角形的周长分为6cm和15cm的两部分，求此三角形的腰和底边的长.

6、所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63º

，求∠DAC的度数．

7、图所示,已知∠1=∠2,∠3=∠4,∠C=32°

∠D=28°

求∠P的度数.

8、已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角为50°

，则∠BAC的度数为。

9如图，把△ABC的纸片沿着DE折叠．

（1）若点A落在四边形BCDE的内部点A′的位置．（如图1）且∠1=40°

，∠2=24°

，求：

∠A′的度数；

（2）若点A落在四边形BCDE的外部（BE的上方）点A′的位置（如图2），则∠A′与∠1，∠2有怎样的关系？

请说明你的理由；

（3）若点A落在四边形BCDE的外部（CD的下方）点A′的位置（如图3），∠A′与∠1，∠2又有怎样的关系？

直接写出你的结论．

10、，∠MON=90°

，点A、B分别在射线OM、ON上移动，BD是∠NBA的平分线，BD的反向延长线与∠BAO的平分线相交于点C．试猜想：

∠ACB的大小是否随A、B的移动发生变化？

如果保持不变，请给出证明；

如果随点A、B的移动发生变化，请给出变化范围．

11、如图

（1），在△ABC中，∠C＞∠B，AD⊥BC于点D，AE平分∠BAC，你能找出∠EAD与∠B、∠C之间的数量关系吗？

并说明理由．

（2）如图

（2），AE平分∠BAC，F为AE上一点，FM⊥BC于点M，这时∠EFM与∠B、∠C之间又有何数量关系？

请你直接说出它们的关系，不需要证明．

12、（09•顺义区一模）取一副三角板按图1拼接，固定三角板ADC，将三角板ABC绕点A依顺时针方向旋转一个大小为α的角（0°

＜α≤45°

）得到△ABC′，如图所示．

试问：

（1）当α为多少度时，能使得图2中AB∥DC；

（2）连接BD，当0°

时，探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况，并给出你的证明．

13、探索：

在图1至图3中，已知△ABC的面积为a，

（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA．若△ACD的面积为S1，则S1=（用含a的代数式表示）

（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE．若△DEC的面积为S2，则S2=（用含a的代数式表示）

（3）在图2的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3=（用含a的代数式表示），并运用上述

（2）的结论写出理由．

发现：

像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的倍．

应用：

要在一块足够大的空地上栽种花卉，工程人员进行了如下的图案设计：

首先在△ABC的空地

上种红花，然后将△ABC向外扩展三次（图4已给出了前两次扩展的图案）．在第一次扩展区域内种谎话，第二次扩展区域内种紫花，第三次扩展区域内种蓝花．如果种红花的区域（即△ABC）的面积是10平方米，请你运用上述结论求出：

（1）种紫花的区域的面积；

（2）种蓝花的区域的面积．

14、已知△ABC中，∠BAC=100°

．

（1）若∠ABC和∠ACB的角平分线交于点O，如图1所示，试求∠BOC的大小；

（2）若∠ABC和∠ACB的三等分线（即将一个角平均分成三等分的射线）相交于O，O1，如图2所示，试求∠BOC的大小；

（3）如此类推，若∠ABC和∠ACB的n等分线自下而上依次相交于O，O1，O2…，如图3所示，试探求∠BOC的大小与n的关系，并判断当∠BOC=170°

时，是几等分线的交线所成的角．

15、如图，DC平分∠ADB，EC平分∠AEB

（1）如图1，若∠DAE=50°

，∠DBE=130°

，求∠DCE；

（2）如图2，若∠DAE=α，∠DBE=β，求∠DCE（用α，β表示）