圆形薄板在均布载荷作用下的挠度Word格式.docx
《圆形薄板在均布载荷作用下的挠度Word格式.docx》由会员分享,可在线阅读,更多相关《圆形薄板在均布载荷作用下的挠度Word格式.docx(16页珍藏版)》请在冰豆网上搜索。
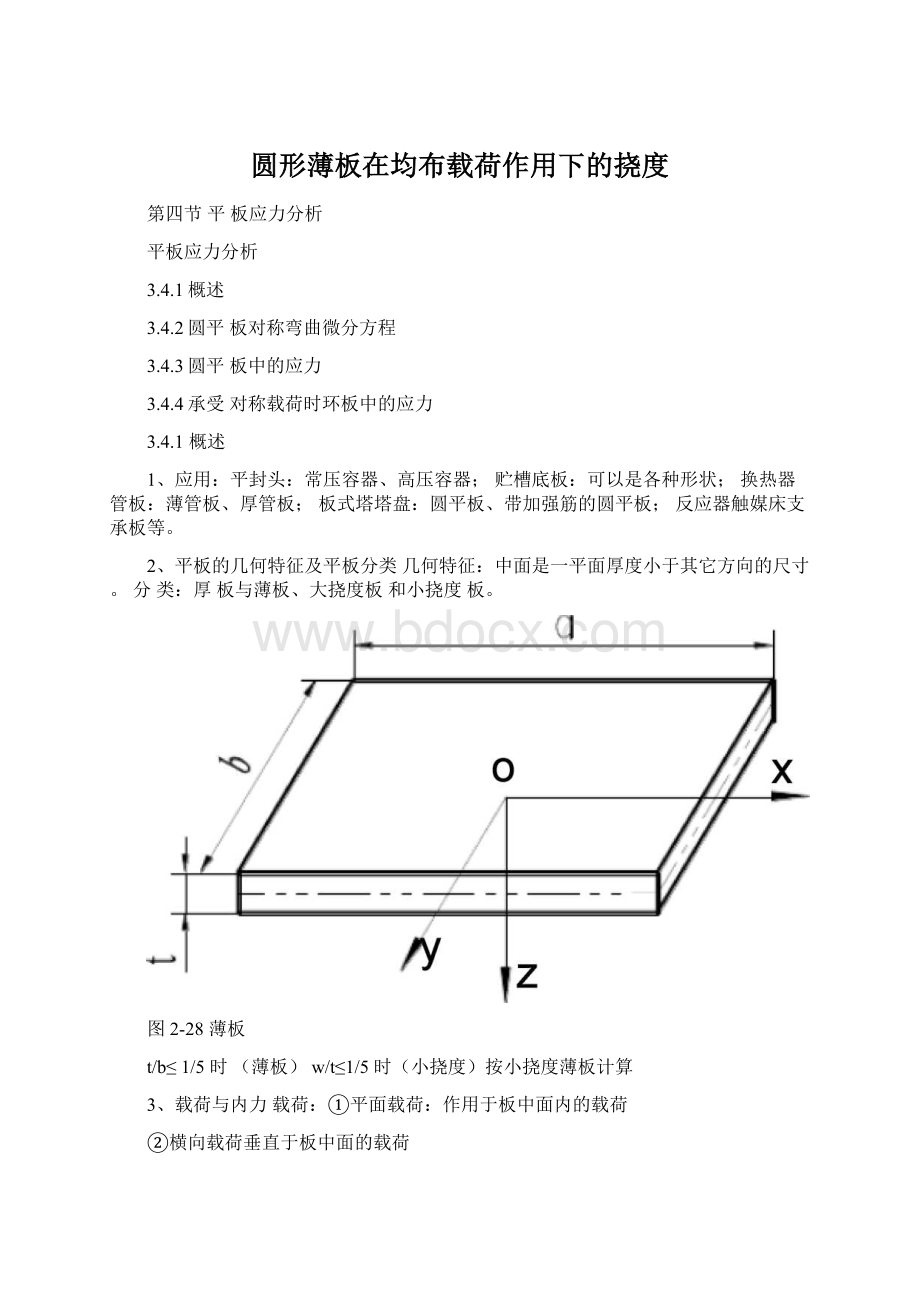
①薄膜力——中面内的拉、压力和面内剪力,并产生面内变形
②弯曲内力——弯矩、扭矩和横向剪力,且产生弯扭变形
◆当变形很大时,面内载荷也会产生弯曲内力,而弯曲载荷也会产生面内力,所以,大挠度分析要比小挠度分析复杂的多。
◆本书仅讨论弹性薄板的小挠度理论。
4、弹性薄板的小挠度理论基本假设---克希霍夫Kirchhoff
①板弯曲时其中面保持中性,即板中面内各点无伸缩和剪切变形,只有沿中面法线w的挠度。
只有横向力载荷
②变形前位于中面法线上的各点,变形后仍位于弹性曲面的同一法线上,且法线上各点间的距离不变。
类同于梁的平面假设:
变形前原为平面的梁的横截面变形后仍保持为平面,且仍然垂直于变形后的梁轴线。
③平行于中面的各层材料互不挤压,即板内垂直于板面的正应力较小,可忽略不计。
◆研究:
弹性,薄板/受横向载荷/小挠度理论/近似双向弯曲问题
3.4.2圆平板对称弯曲微分方程
分析模型
分析模型:
半径R,厚度t的圆平板受轴对称载荷Pz,在r、θ、z圆柱坐标系中,内力Mr、Mθ、Qr三个内力分量
轴对称性:
几何对称,载荷对称,约束对称,在r、θ、z圆柱坐标系中,挠度w只pz
是r的函数,而与θ无关。
求解思路:
经t/2一系列推导(基于平衡、几何、物理方程)→弯r曲挠度微分方程(pz:
w)
t/2
→求w求→内力
M→求应力
z
微元体:
用半径为r和r+dr的圆柱a面.和夹角为dθ的两个径向截面截取板上一微元体
微元体内力
径向:
Mr、Mr+(dMr/dr)dr
周向:
Mθ、Mθ
横向剪力:
Qr、Qr+(dQr/dr)dr
微元体外力:
上表面Ppzrddr
1、平衡方程
dr
Qr
d.
za.
Qrdr
圆平板在轴对称载y荷下的平衡方程)c.
2、几何协调方程(W~ε)
取ABdr,径向截面上与中面相距为z,半径为r与rdr两点A与B构成的微段
板变形后:
应变与挠度关系的几何方程:
d2w
rzdr2
dr(2-55)
zdw
rdr
3、物理方程
根据第3个假设,圆平板弯曲后,其上任意一点均处于两向应力状态。
由广义虎克
定律可得圆板物理方程为:
2-56)
4、圆平板轴对称弯曲的小挠度微分方程
(2-55)代入(2-56)式:
Ezd2wdw
2-57)
r12dr2rdr
2
Ez1dwdw
12rdrdr2
可见,r和沿着厚度(即z方向)均为线性分布,图2-31中所示为径向应力的分布图
图2-31圆平板内的应力与内力之间的关系
的线性分布力系便组成弯矩Mr、M。
单位长度上的径向弯矩为:
t2E
d2w
dw
z2dz
21
2dr2
t
Mr2trzdz
参照38页壳体的抗弯刚度,——“抗弯刚度”与圆板的几何尺寸及材料性能有关
(2-58)代入(2-57),得弯矩和应力的关系式为:
12Mr
2-59)
12tM3rz12M
t3z
即:
受轴对称横向载荷圆形薄板小挠度弯曲微分方程:
d1dd
r
drrdrdr
D
2-60)
Qr值可依不同载荷情况用静力法求得
3.4.3圆平板中的应力(圆平板轴对称弯曲的小挠度微分方程的应用)
承受均布载荷时圆平板中的应力:
①简支②固支
承受集中载荷时圆平板中的应力
图2-32均布载荷作用时圆板内Qr的确定
、承受均布载荷时圆平板中的应力
据图2-32,可确定作用在半径为r的圆柱截面上的剪力,即:
rppr
2r2
代入2-60式中,得均布载荷作用下圆平板弯曲微分方程为:
d1ddwrdrrdrdr
pr
2D
对r连续两次积分得到挠曲面在半径方向的斜率:
3
dwprC1rC2dr16D2r
2-61)
对r连续三次积分,得到中面在弯曲后的挠度
4pr464D
C1r
C2lnrC3
2-62)
C2
因而要求积分常数
C1、C2、C3均为积分常数。
对于圆平板在板中心处(r=0)挠曲面之斜率与挠度均为有限值,=0,于是上述方程改写为:
式中C1、C3由边界条件确定
下面讨论两种典型支承情况(两种边界条件)
①周边固支圆平板
②周边简支圆平板
p
R
a.b.
周边固支圆平板周边简支圆平板图2-33承受均布横向载荷的圆板
pR2
8D
pR4
64D
1、周边固支圆平板:
(在支承处不允许有挠度和转角)
周边固支圆平板
rR,0
rR,w0
C1将上述边界条件代入式(2-63),解得积分常数:
C3
代入式(2-63)得周边固支平板的斜率和挠度方程:
dwdrw
prR2
16D
22
R2r2
2-64)
将挠度w对r的一阶导数和二阶导数代入式(2-58),便得固支条件下的周边固支
圆平板弯矩表达式:
Mr
16
R21
r23
M
r213
2-65)
由此(代入2-59)弯曲应力计算试,可得r处上、下板面的应力表达式:
周边固支圆平板下表面的应力分布,如图2-34(a)所示
图2-34圆板的弯曲应力分布(板下表面)
2、周边简支圆平板
将上述边界条件代入式(2-63),解得积分常数C1、C3:
代入式(2-63)得周边简支平板的挠度方程:
222R2r224R2R2r2
2-67)
b.
周边简支圆平板
弯矩表达式:
Mrp3R2r2
2-68)
r16
MpR23r213
应力表达式:
m3p23R2r2
2-69)
8t2
3p22
m2R3r13
可以看出,最大弯矩和相应的最大应力均在板中心处r0,
周边简支板下表面的应力分布曲线见图2-34(b)。
a.
b.图2-34圆板的弯曲应力分布(板下表面)
3、比较两种支承
a.边界条件
周边固支时:
R,
0dr
w0
周边简支时:
Mr0
b.挠度
c.
2-70)
2-71)
表明:
周边简支板的最大挠度远大于周边固支板的挠度
d.应力
周边固支圆平板中的最大正应力为支承处的径向应力,其值为
f
rmax
3pR2
4t2
2-72)
周边简支圆平板中的最大正应力为板中心处的径向应力,其值为
表明:
周边简支板的最大正应力大于周边固支板的应力
内力引起的切应力:
在均布载荷p作用下,圆板柱面上的最大剪力
max
pR
p2R(r
R处),
近似采用矩形截面梁中最大切应力公式
3Q
2bh
得到3Qrmax3pR
得到max
21t4t
2最大正应力与Rt2同一量级;
最大切应力则与Rt同一量级。
因而对于薄板R>
>
t,板内的正应力远比切应力大。
从以上可以看出:
max与wmax圆平板的材料(E、μ)、半径、厚度有关•若构成板的材料和载荷已确定,则减小半径或增加厚度都可减小挠度和降低最大正
应力。
•工程中较多的是采用改变其周边支承结构,使它更趋近于固支条件•增加圆平板厚度或用正交栅格、圆环肋加固平板等方法来提高平板的强度与刚度
4、结论
a.板内为二向应力状态:
r、且为弯曲应力,平行于中面各层相互之间的正应力z及剪力Qr引起的切应力均可予以忽略。
b.应力分布:
沿厚度呈线性分布,且最大值在板的上下表面。
沿半径呈抛物线分
布,且与周边支承方式有关
工程实际中的圆板周边支承是介于两者之间的形式。
c.强度:
e.刚度:
∴周边固支的圆平板在刚度和强度两方面均优于周边简支圆平板
f.薄板结构的最大弯曲应力max与Rt成正比,而薄壳的最大拉(压)应力max与Rt成正比。
故在相同Rt条件下,薄板所需厚度比薄壳大。
、承受集中载荷时圆平板中的应力
挠度微分方程式(2-60)中,剪力Qr可由图2-35中的平衡条件确定:
Qr2Fr
采用与求解均布载荷圆平板应力相同的方法,可求得周边固支与周边简支圆板的挠度
和弯矩方程及计算其应力值
图2-35圆板中心承受集中载荷时板中的剪力Qr
3.4.4承受轴对称载荷时环板中的应力
◆通常的环板仍主要受弯曲,仍可利用上述圆板的基本方程求解环板的应力、应变,只是在内孔边缘上增加了一个边界条件。
◆当环板内半径和外半径比较接近时,环板可简化为圆环。
圆环在沿其中心线(通过形心)均布力矩M作用下,矩形截面只产生微小的转角而无其它变形,从而在圆环上
产生周向应力。
这类问题虽然为轴对称问题,但不能应用上述圆平板的基本方程求解。
R1
设圆环的内半径为Ri、外半径为Ro、形心处的半径为Rx、厚度t,沿其中心线(通
过形心)均布力矩M的作用,如图2-37所示。
文献[40]给出了导出圆环绕其形心的转角
和最大应力max(在圆环内侧两表面)
12MRx
Et3lnRo
Ri(2-74)
6MRx
t2RilnRo
iRi
图2-37圆环转角和应力分析