回归分析作业参考答案Word格式文档下载.docx

资源描述

回归分析作业参考答案Word格式文档下载.docx

《回归分析作业参考答案Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《回归分析作业参考答案Word格式文档下载.docx（26页珍藏版）》请在冰豆网上搜索。

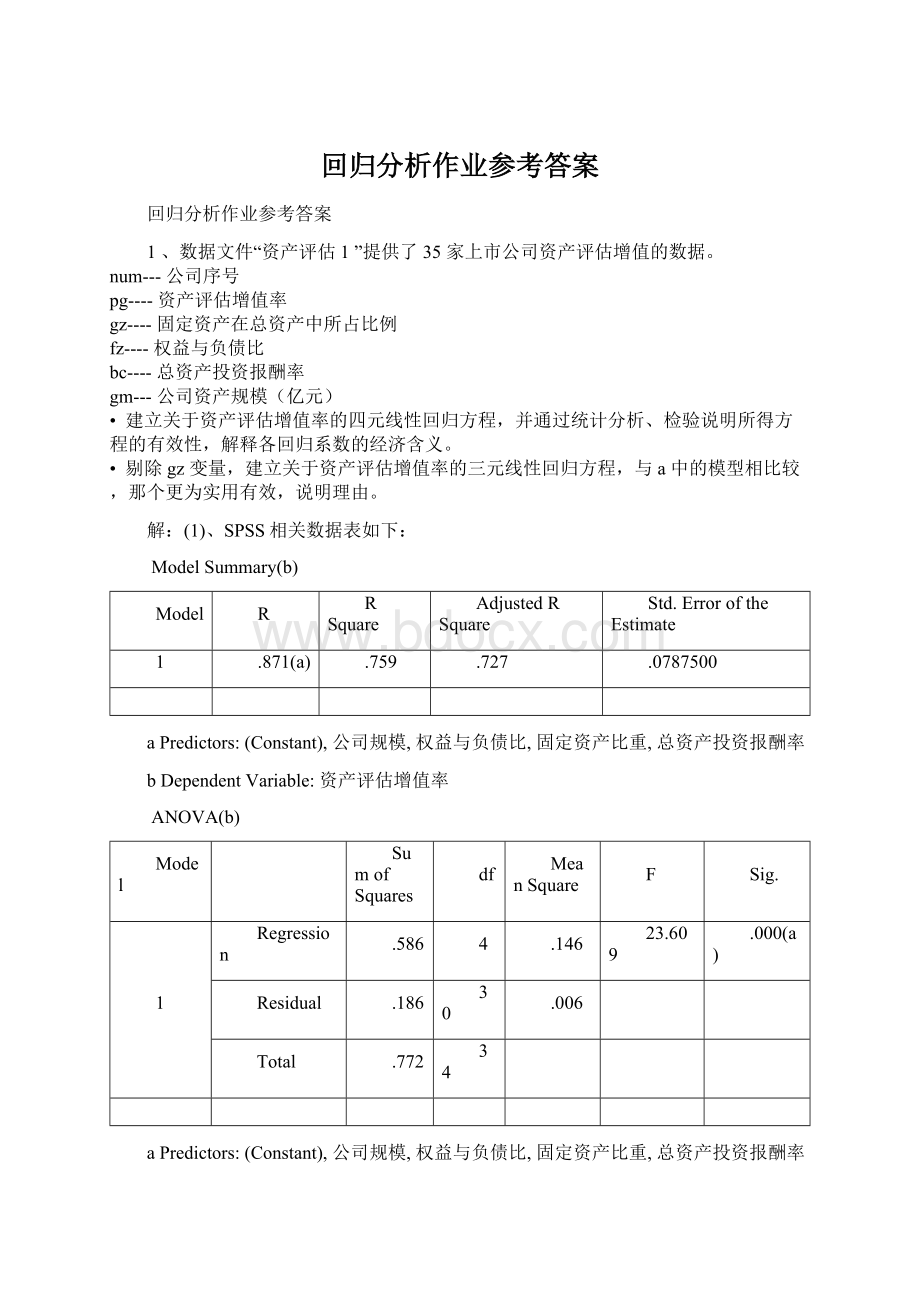
回归分析作业参考答案Word格式文档下载.docx

Residual

.186

.006

Total

.772

ResidualsStatistics（a）

Minimum

Maximum

Mean

Std.Deviation

PredictedValue

-.084652

.494055

.172240

.1312429

-.150002

.149380

.000000

.0739727

Std.PredictedValue

-1.957

2.452

.000

1.000

Std.Residual

-1.905

1.897

.939

aDependentVariable:

R为0.871，决定系数R2为0.759，校正决定系数为0.727。

拟合的回归模型F值为23.609，P值为0，所以拟合的模型是有统计意义的。

从系数的t检验可以看出，只有固定资产比重的相伴概率0.339>

0.05，说明只有固定资产比重对资产评估增值率的影响是不显著的，其他自变量对固定资产增值的比率均有显著的影响。

线性回归方程为：

pg=0.396+0.079gz+0.063fz+0.602bc-0.044gm

表示，在权益与负债比、总资产投资报酬率和公司规模不变的条件下，固定资产比重每增加1个单位，资产评估增值率增加

。

表示，在固定资产比重、总资产投资报酬率和公司规模不变的条件下，权益与负债比每增加1个单位，资产评估增值率增加

表示，在固定资产比重、权益与负债比和公司规模不变的条件下，总资产投资报酬率每增加1个单位，资产评估增值率增加

表示，在固定资产比重、权益与负债比和总资产投资报酬率不变的条件下，公司规模每增加1亿元，资产评估增值率减少

（2）、SPSS相关数据表如下：

.867（a）

.751

.0786809

（Constant）,公司规模,权益与负债比,总资产投资报酬率

.580

.193

31.218

.192

ResidualsStatistics（a）

-.062589

.511513

.1305841

-.161246

.145304

.0751295

-1.798

2.598

-2.049

1.847

.955

相关系数R为0.867，决定系数R2为0.751，校正决定系数为0.727。

从系数的t检验可以看出，该模型的回归系数都通过检验。

所以，剔除gz变量，建立关于资产评估增值率的三元线性回归方程为：

pg=0.376+0.063fz+0.600bc-0.040gm

b更为有效实用，因为所有的回归系数都通过了t检验，并且b模型估计的标准误较小。

2、数据文件“房产销售”提供了20件房地产的销售价格和评估的数据（美元）：

y----销售价格；

x1----地产评估价值；

x2----房产评估价值；

x3----面积（平方英尺）。

建立适当的关于销售价格的多元线性回归模型.

利用模型预测地产评估价值为2000，房产评估价值为12000，面积为1100的销售价格，并给出预测值的95%的置信区间。

通过对模型的统计检验说明预测值的可信度。

通常先做enter，然后做逐步

（1）对原数据进行回归分析，得到回归方程为：

y=105.382+0.961x2+16.348x3

（2）地产评估价值为2000，房产评估价值为12000，面积为1100的销售价格的95%的置信区间为：

（21468.99197，37776.93332）。

（3）该模型的AdjustedRSquare=0.867，也就是这两个自变量可以解释86.7%的因变量变差，应该说是预测的可信度比较高；

并且残差符合正态性、独立性和方差齐次性，模型成立，即有95%的可能性b的预测值在区间21468.99197-37776.93332内。

3、

大多数公司都提供了β估计值，以反映证券的系统风险。

一种股票的β值所测量的是这种股票的回报率与整个市场平均回报率之间的关系。

这个指标的名称就来自简单线性回归中的斜率参数β。

在这种回归中，因变量是股票回报率（Y）。

而自变量则是市场回报率（X）。

值大于1的股票被称为“攻击性”证券，因为它们的回报率变动（向上或向下）得比整个市场的回报率快。

相反，β值小于1的股票被称为“防御性”证券，因为它们的回报率变动的比市场回报率慢。

值接近1的股票被称为“中性”证券，因为它们的回报率反映市场回报率。

下面表中的数据是随机抽选的7个月内某只特定的股票的月回报率及整个市场的回报率。

试对这些数据完成简单线性回归分析。

根据你的分析结果，你认为这只股票是属于攻击性，防御性，还是中性的股票？

回归模型：

y=1.762x-1.329。

β值为线性回归斜率参数1.762>

1，所以，该股票属于“攻击性股票”。

4、参考上题。

股票的β值是否依赖于计算回报率的时间长度？

因为有些经济商号用的是按月数据计算的β值，另一些经济商号则用按年数据计算的β值，所以这个问题对投资者来说很重要。

H.莱维分别研究了三类股票的时间长度（月）和平均β值。

将时间长度从一个月逐步增加到30个月，莱维计算了1946---1975年间144只股票的回报率。

根据他所得的β值，这144只股票中有38只攻击性股票，38只防御性股票，以及68只中性股票。

下表中给出的这三类股票对不同时间水平的平均β值。

对于攻击性股票、防御性股票和中性股票三种情况，分别求表达平均β值Y与时间长度X之间关系的最小二乘简单线性回归方程。

对每一类股票检验假设：

时间长度是平均β值的有效线性预测器，检验时用α=0.05。

对每一类股票，构造直线斜率的95%置信区间，哪只股票的β值随时间长度的增大而线性增大？

（1）攻击性股票：

系数a

模型

非标准化系数

标准系数

标准误差

试用版

（常量）

1.451

.059

24.392

时间长度

.016

.004

.856

4.377

.003

a.因变量:

攻性型股票

回归方程：

Y1=1.451+0.016X

防御性股票：

.459

.013

34.178

-.005

.001

-.901

-5.488

防御性股票

Y2=0.459-0.005X

中性股票：

.911

.025

37.083

.009

.002

.906

5.672

中性股票

Y3=0.911+0.009X

（2）（3）攻击型股票：

B的95.0%置信区间

下限

上限

1.310

1.591

.007

直线斜率的95%的置信区间为（0.007，0.025）

.428

.491

-.007

-.003

直线斜率的95%的置信区间为（-0.007，-0.003）

.853

.969

.005

.012

直线斜率的95%的置信区间为（0.005，0.012）

时间长度的t检验P值分别为0.003、0.001、0.001均小于0.05，所以，拒绝原假设，即线性关系显著。

从上面三张表中，我们通过观察系数95%的置信区间，得出攻击性和中性股票的β值随时间长度的增大而线性增大。

5个人计算机（PC机）正以非凡的技术在发展，PC机的零售价格也是这样。

由于购买时间和机器特点不同，一台PC机的零售价格可能发生戏剧性的变化。

不久前收集了一批IBMPC机和IBMPC兼容机的零售价格数据，共有N=60，见数据文件“计算机价格”。

这些数据被用来拟合多元回归

E（Y）=β0+β1x1+β2x2

其中：

Y=零售价格（美元）

x1=微处理器速度（兆赫）

试写出最小二乘预测方程。

此模型是否适合于预测？

用α=0.10进行检验。

构造β1的90%置信区间，并对此区间作出解释。

本模型中的CPU芯片（x2）是否是价格（Y）的有效预测器？

用α=0.10进行预测。

Correlations

价格y

速度

分组

PearsonCorrelation

.607

.284

.371

Sig.（1-tailed）

.015

ModelSummary

.610a

.373

.350

962.967

a.Predictors:

（Constant）,分组,速度

ANOVAb

3.083E7

1.541E7

16.622

.000a

5.193E7

927305.918

8.276E7

b.DependentVariable:

价格y

Coefficientsa

UnstandardizedCoefficients

StandardizedCoefficients

95.0%ConfidenceIntervalforB

Std.Error

Beta

LowerBound

UpperBound

Zero-order

Partial

Part

（Constant）

642.477

481.312

1.335

.187

-321.707

1606.660

108.237

21.198

.582

5.106

65.772

150.702

.564

.540

248.597

417.408

.068

.596

.554

-587.573

1084.766

.079

.063

a.DependentVariable:

最小二乘预测方程为：

E（y）=642.477+108.237X1+248.597X2

此模型中常量和芯片的t检验P值大于0.10不能拒绝原假设，即线性关系不显著。

故在α=0.10的条件下，此模型并不适合于预测。

β1的90%置信区间为（72.783，143.691）。

这表示，1个单位的速度变化量对价格产生的影响有90%的概率在72.783—143.691之间。

CPU芯片（x2）不是价格（Y）的有效预测器。

6、在工厂中，准确估计完成一项作业所需的工时数对于诸如决定雇佣工人的数量，确定向客户报价的最后期限，或者作出与预算有关的成本分析决策等决策管理来说是极端重要的。

一名锅炉筒制造商想预测在一些在未来预测项目中装配锅炉筒所需的工时数。

为了用回归方法实现此目标，他收集了35个锅炉的项目数据（数据文件“锅炉”）。

除工时（Y）外，被测量的变量有锅炉工作容量（X1=磅/小时），锅炉设计压力（X2=磅/平方英寸），锅炉的类型（X3=1，如在生产领域装配；

X3=0，如在使用领域装配），以及炉筒类型（X4=1，蒸汽炉筒；

X4=0，液体炉筒）。

试检验假设：

锅炉容量（X1）与工时数（Y）之间有正线性关系。

锅炉压力（X3）与工时数（Y）之间有正线性关系。

构造β1的95%置信区间并对结果做出解释。

构造β3的95%置信区间。

此题题目有误：

第二小题应该是“锅炉压力（X2）与工时数（Y）之间有正线性关系”

A绘制锅炉容量（X1）与工时数（Y）的散点图，由散点图看到，锅炉容量（X1）与工时数（Y）之间有一定的线性相关关系，但不明显；

对两个变量继续作相关分析，通过检验认为；

锅炉容量（X1）与工时数（Y）之间有正线性关系。