随机过程习题第4章01Word文档下载推荐.docx
《随机过程习题第4章01Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《随机过程习题第4章01Word文档下载推荐.docx(29页珍藏版)》请在冰豆网上搜索。
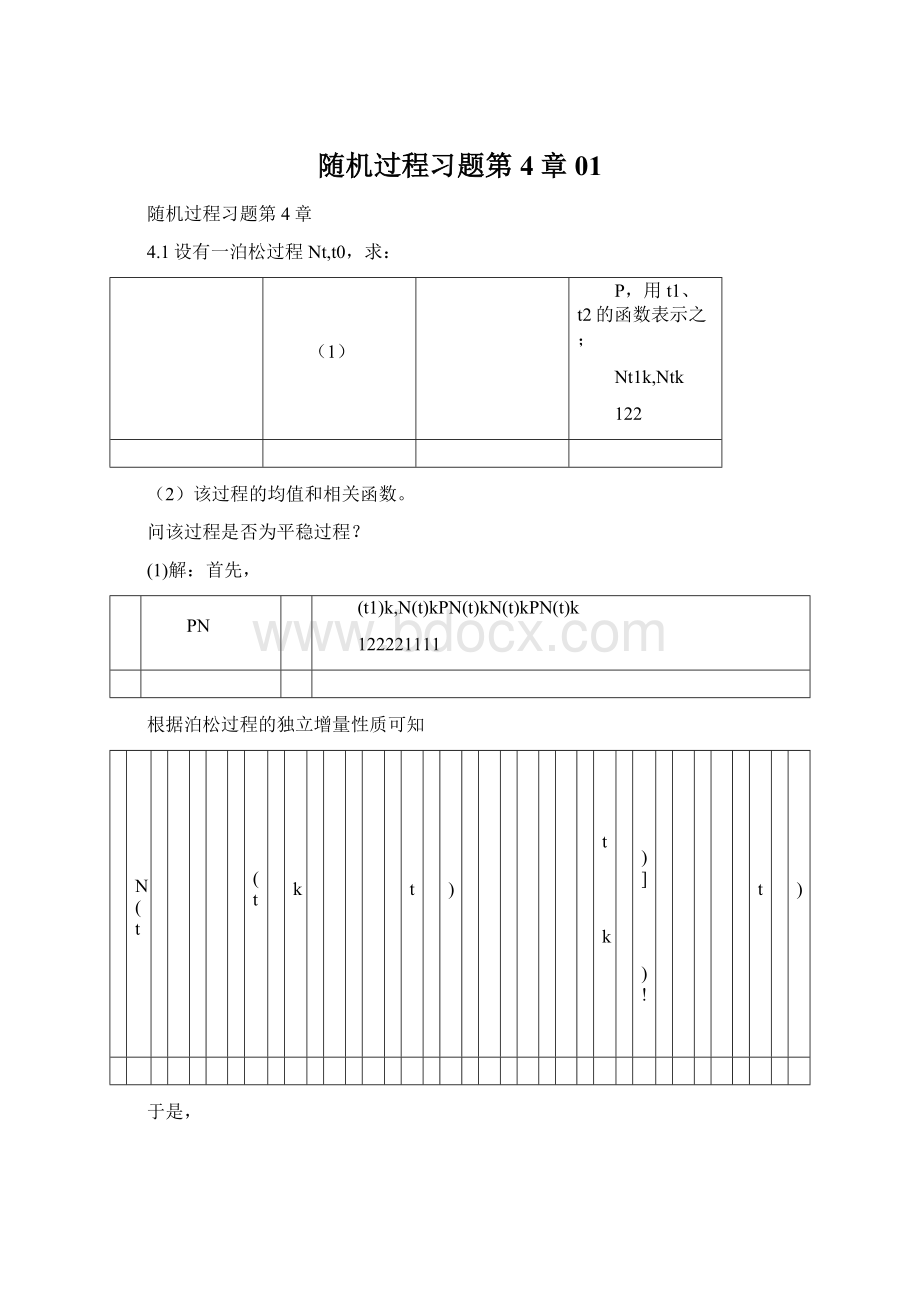
(t)t
tt
kete
0!
k1!
k1
根据泊松过程的独立增量过程性质可得其相关函数为(t2t1)
EN
(t)
E
E[N
(t)]E[
N(t)]
E[
)]
其中,
[N(t2)N(t1)](t2t1)
E[Nttt
2()]22
111
于是,t2t1时的相关函数为
2222
N(t1)N(t)t(tt)ttttt
212111121
同理可得t1t2时的相关函数为
(tNtttt
1)()
2122
4-1
所以,泊松过程的相关函数为
N(tNttttt
1)()min,
21212
所以,泊松过程过程不是平稳过程。
4.2设有一个最一般概念的随机电报信号{(t)},它的定义如下:
(1)(0)是正态分布的随机变量N(0,2);
(2)时间内出现电报脉冲的个数服从泊松分布,即
()
P{k,}e(k=1,2,⋯)
(3)不同时间的电报脉冲幅度服从正态分布N(0,2),这个脉冲幅度延伸到下
一个电报脉冲出现时保持不变,不同电报脉冲幅度的取值是相互统计独立
的,同一电报脉冲内幅度是不变的。
(4)不同时间间隔内出现电报脉冲的个数是相互统计独立的。
它的样本函数如图4-2。
(k)(t)
图4-2
(1)试求它的二元概率密度。
(2)试问该过程是否平稳?
设t1<
t2,t1和t2时刻的脉冲幅度之间的关系有两种情况:
①t1和t2处于同
一脉冲内;
②t1,和t2不处于同一脉冲内。
对于情况②,由于不同脉冲内的幅度取值
是相互统计独立的,因此两时刻的脉冲幅度间的联合概率密度函数为
f(t1(x1)f(t2)x2
(
4-2
其中,f(t)
(1)和f(t)
(2)分别是(t)在t1和t2时刻的概率密度函数。
发生情况②
1x2x
的概率就是t1和t2两个时刻间的脉冲变化次数大于等于1的概率,即
Pr{t1t}e1e,tt
和处于不同脉冲内
21
显然,t1和t2处于同一脉冲内的概率为e。
在这种情况下,两时刻的脉冲幅度间
的联合概率密度函数为
ft
(1)(21
(1xxx
因此,t1和t2时刻的脉冲幅度的联合概率密度函数为
f
(x,
x)
[1e
]
exp
x
(2).由此可见该过程是平稳过程,并且可以推导其多维PDF也是只与各时刻间的间
隔有关,因此是严平稳过程。
4.3设1、2为独立同分布随机变量,且均匀分布于(0,1)上,又设有随机过程
(t)1sin(2t)
求
(1)(t)均值;
(2)(t)的相关函数
由于1、2是独立的,因此
E[(t)]E[1sin(2t)]E[1]E[sin(2t
1、2都均匀分布于(0,1)上,所以
E]
[1
E[sin(
sin(t)d
022
cost
E[(t)]
cos
2t
(2)相关函数为
4-3
E[2122
()()][)(
t1tE]E[sin(tsint
其中
[2
3
和
t)sin
22
{cos[(tt)]cos[(tt)]}d
02122122
sin(t
212
所以,
6
4.4设(t)是实正态分布平稳随机过程,它的数学期望为0。
如定义
|
试证明
E()}cos
{t1k
22C代表(t)的方
k,C()代表(t)的协方差函数,(0)
()C()/
差。
证明:
由给出的(t)定义式可知它有两种可能的取值,即
1,(t)(t)0(t)
0,(t)(t)0
因为(t)是实正态平稳随机过程,且均值为0,所以联合正态分布为
ftt
()(
(x,y)
1x
1r
2rxy
(1
r
y
2k
rC()/()
参考《概率随机变量和随机过程》(西安电子科技大学译本)之第226至229页可以
4-4
得
P{(t)(t)0}
arcsinr
因此,(t)的均值为
E{(t)}1P{(t)(t)0}0P{(t)(t)0}
arccos(r)cos
1k
4.5设有随机过程(t)zsin(t),(t)。
其中,z,是相互独立的随机变
量,
P{},
42
P{},Z均匀分布于(-1,1)之间。
试证明(t)是宽
平稳随机过程,但(t)不满足严平稳的条件(不满足一级严平稳的条件)。
由Z均匀分布于(-1,1)之间得
E]0,[
[zEz2
并且z和相互独立。
所以,(t)的均值为
E[(t)]E[z]E[sin(t)]0
(t)的相关函数为
R[
z
]E[sin(t)sin(t
cos(t
cos(tt
由此可见,(t)的均值为常数,相关函数只与时间差t2t1有关。
因此,随机过程(t)
4-5
是宽平稳随机过程。
证明严平稳可以用特征函数,(t)的一维特征函数为
juzsin(t)
E[e]
Z
4
[e]
E[e
juzsin(t
d
juz
sin[usin(t)]sin[usin(t)]
44
jusin(t)jusin(t)
与时间t有关(如下图所示),因此(t)不是严平稳。
4.6设z为随机变量,为另一随机变量,z与相互统计独立,均匀分布于(0,2)
间;
又设有随机过程
(t)zsin(t)(t)
其中为常数,0,试利用特征函数证明(t)是一严平稳随机过程。
因为特征函数能唯一地确定概率密度函数,若能证明(t)的k阶特征函数具有
4-6
时移不变性,即
(u1,u2,,uk;
t1,t2,,tk)(u1,u2,,uk;
t1,t2,,tk)
则其k维概率密度函数是时移不变的。
如果对于任意k都成立,则该过程是严平稳
的。
该随机过程中包含z和两个随机变量,且z与相互统计独立。
因此,其特征
函数可以分两步求解。
首先,令za,对求均值,然后再对z求均值。
由于均匀
分布于(0,2)间,即
f(),于是
kk
Ei
{exp[ju(t)]za}exp[juasin(t)]
iii
i1i1
令。
则
E{exp[ju(t)]za}exp[juasin(ti)]
上式中的被积函数是的周期函数,周期为2。
因此,
E{exp[j
u(t)]z
ii
a}
i1
exp[j
u
i
asin(
(t)]z
E{i
E{exp[ju(t)]z}}E{E{exp[ju(t
ZiiZi
)]z}}
即
ui(t)]}E{exp[ju(t
)]}
由此可见,(t)的k阶特征函数具有时移不变性,即(t)为严平稳随机过程。
4.7设有一相位调制的正弦信号,其复数表示式为
4-7
(t)e
j
(t(tt
))
其中,为常数,>
0,(t)是一个二级严平稳过程,设t1t(u1,u2)是过程(t)的二
维特征函数,即
t1(u,u)Ee
t12
j[u
同时对于任何,0(1,0)0。
试证明过程(t)是宽平稳过程,并求它的相
关函数R(t1,t2)。
首先,(t)的均值为
jEeee
tj(t)jtjt
E{(,0,
t)}e[1,0]
[1,0]0
R
(t,
E{
)}
j(tt)j[(t)(t)]
1212
eEe
[1,
t,t
1]
因为(t)是一个二级严平稳过程,所以t(1,1)只与t1t2有关。
因此,R(t1,t2)也
1,t
只与t1t2有关,且其均值为常数,所以(t)是宽平稳随机过程。
4.8设有一时间离散的马尔可夫过程(n)(n0,1,2,)。
(0)具有概率密度函数
2x(0x1)
(x)
其它
对于n1,2,3,,当给定(n1)x时(n)的条件概率密度均匀分布于(1-x,1)之
间。
问(n)(n1,2,)是否满足严平稳的条件?
解:
对于任意一个马尔可夫过程和任意m+1个取样点,它们的联合概率密度函数有
如下性质
m1
f(x
jxfxf(xx
,)()1|)
jmjjijijxfxf(xx
i0
对于本题,其中的f(xi1|xi)是不随时刻i变化的。
若f(xi)也是与时刻i无关的,
4-8
则f(xj,,xjm)在时间轴上做任意平移时是不变的,那么该过程是严平稳的。
只需要证明f(xj)与时刻j无关。
首先,
(1)的概率密度函数为
11
ff(y|x)f(x)dx2d2,(0
1yxxyy
11|00
y1y
1)
由此可见,
(1)的概率密度函数与(0)的概率密度函数相同。
依此类推,可得
(n)(n2,3,)的概率密度函数也与(0)的概率密度函数相同,即(n)的概率密度
函数不随时刻i变化。
因此,取样点在时间轴上做任意平移时该过程的所有有限维分
布函数是不变的,即(n)是严平稳过程。
01-y1x
4.9设有两状态时间离散的马尔可夫链(n)(n=1,2,3,⋯),..(n)可取0或1,它的一
步转移矩阵为
q
p
p1+q1=1,p2+q2=1
P{(0)0},
pp
P{(0)1}
试证明该过程为严平稳过程。
对于齐次马尔可夫链,其一步转移概率与时刻无关,若其一维概率分布也与
时刻无关,则其任意维联合概率密度函数只与取样点间的时间间隔有关,而与具体
4-9
的时刻无关,即具有严平稳性质。
因此,对于本题只需要证明该马尔可夫链的一维
概率分布与时刻无关。
首先,
(1)的概率分布为
P{
(1)0}P{
(1)0,(0)0}P{
(1)0,(0)1}
P{
(1)0|(0)0}P{(0)0}P{
(1)0|(0)1}P{(0)1}
qP{
(0)0}
pP{(0)
1}
P{(0)0}
同理可得
P{
(1)1}
ppqp
1221
p1P{(0)0}qP{(0)1}P{
(0)
由于一步转移概率与时刻无关。
所以,由此可以推知
P{(n)1}P{
(1)1}P{(0)1}
P{(n)0}P{
(1)0}P{(0)0}
其中,n=1,2,3,⋯。
..所以该过程为严平稳过程。
此题的另一种解法就是先求n步转移阵,然后直接求n时刻的概率分布。
利用习题2.11的结果可得n步转移阵为
(n)
p(1
n
p)
P{(n)1}
01
P{
0}
PP{
0)
4-10
同理可得,
P{(n)0}P{(0)0}
所以,该过程是严平稳过程。
4.10设有相位调制的正弦过程
(t)Acos[(t(t)]
0,t,t0是泊松过程,A是对称贝努利型随机变量,即
P{A1},
P{A1},A和t是相互统计独立的。
试画出其样本函数,样
本函数是否连续?
求(t)的相关函数R(t1,t2),问是否均方连续?
设t1t2。
由给出的(t)Acos[(t(t)]可得
A
cos[(t(t)]cos[(t
偶数
Acos
奇数
2(t2t)
1e
P{tt偶数}
P{tt奇数}
(t)(t)|A
a]
a