二次函数几何定义题文档格式.docx
《二次函数几何定义题文档格式.docx》由会员分享,可在线阅读,更多相关《二次函数几何定义题文档格式.docx(23页珍藏版)》请在冰豆网上搜索。
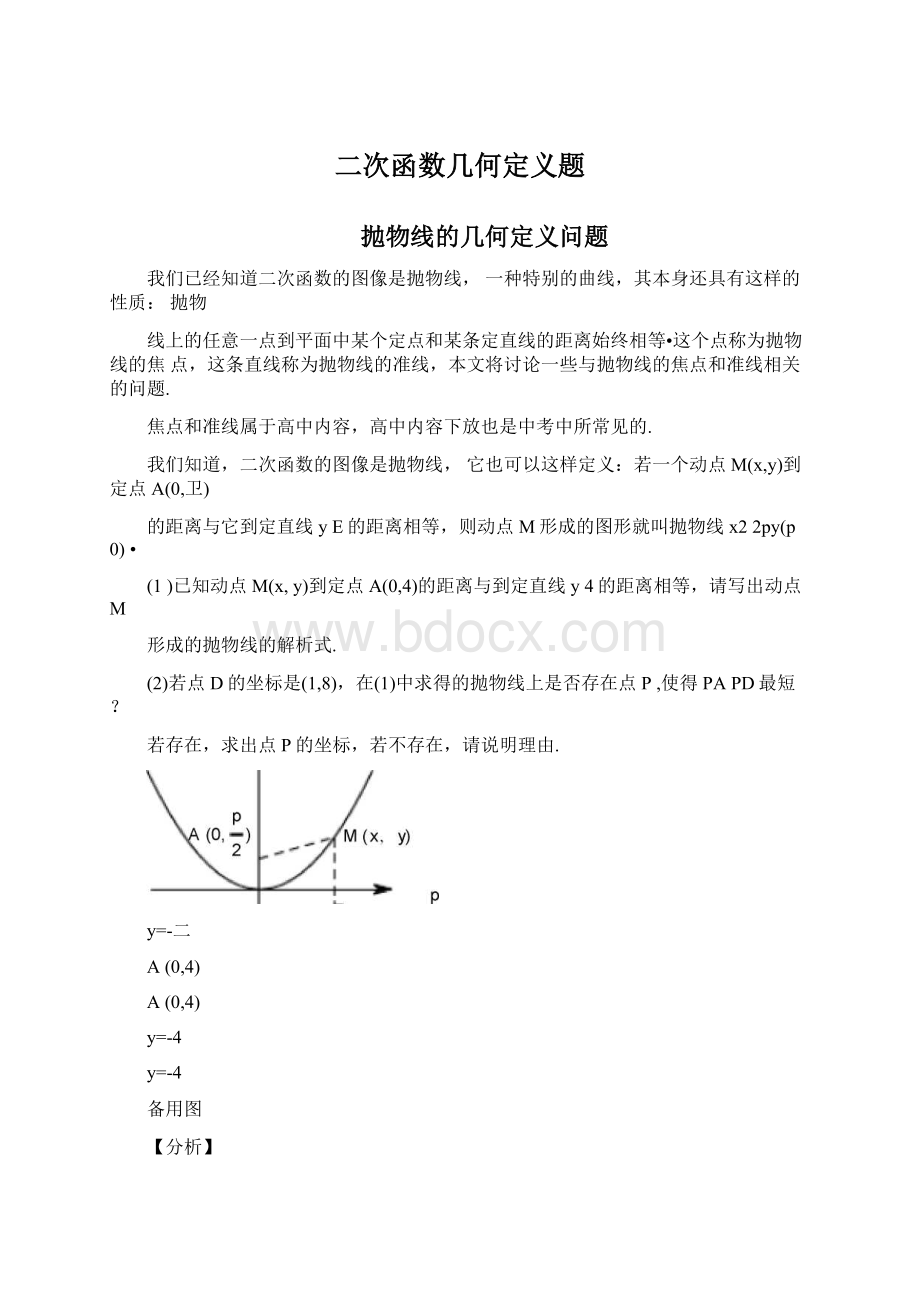
(2018•湘潭中考)
如图,点P为抛物线y—x2上一动点.
4
(1)若抛物线y—x2是由抛物线y—(x2)21通过图像平移得到的,请写出平移的过程;
44
(2)若直线I经过y轴上一点N,且平行于x轴,点N的坐标为(0,1),过点P作PMI
于M.
1问题探究:
如图一,在对称轴上是否存在一定点F,使得PMPF恒成立?
若存在,
求出点F的坐标:
若不存在,请说明理由.
2问题解决:
如图二,若点Q的坐标为(1,5),求QPPF的最小值.
(1)向右平移2个单位,向上平移1个单位;
(2)①直线I即为抛物线的准线,所求F点为焦点.
考虑特殊位置,当P点在顶点时,可得F点坐标为(0,1)或(0,-1)(舍掉),以下证明P在抛物线任意位置,均满足PF=PM:
12
设P点坐标为m,-m
则
PF.
m02
1
2.
m1
J
12-m1
2m21,
V
又
PM
-m21
-m1
m1,
•••PF=PM,
•••当F点坐标为(0,1)时,PM=PF恒成立.
②由①可得PQ+PF=PQ+PM,
过点Q作QM丄x轴,与x轴交点即为M点,与抛物线交点为P点,
此时PQ+PM=QM=6,故QP+PF的最小值为6.
(2019自贡删减)
如图,已知直线AB与抛物线C:
yax22xc相交于点A(1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)在抛物线C的对称轴上是否存在定点F,使抛物线C上任意一点P到点F的距离等于
17
到直线y—的距离?
若存在,求出定点F的坐标;
(1)函数解析式:
y
x2*
2x3
(2)问题已经很明显了,
—是抛物线准线,我们要求的F是焦点.
易求抛物线对称轴为直线
x=1,不妨取特殊位置得到结果,再证明.
当点p在抛物线顶点时,
P点坐标为(1,4),此时点P到直线y
171
-的距离为-,
故此时点P到点F的距离也为!
,满足条件的F点坐标有1,15
4'
考虑到吧在直线y147上,故需舍去,
F点可能的坐标只有1,15,
的距离.
接下来证明,P在抛物线任意位置,均满足PF等于P到直线y
设P点坐标为m,n
,过P点作PQ丄直线y17,垂足记为Q点,
则PQ=n17,又
PF
15
•••点P在抛物线上,
2m
4nn—
n—
即PF=PQ,
所以当F点坐标为
1罟时,点P在抛物线任意位置,均满足
PF等于P到直线
y一的距离.
(2018•宜宾删减)
在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线
y-x与抛物线交于A、B两点,直线I为y1.
(1)求抛物线的解析式;
(2)知Fxo,yo为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线I的距离与
点M到点F的距离总是相等,求定点F的坐标.
(1)抛物线:
y丄x22;
(2)不难猜测直线I是抛物线的准线,所求F点为抛物线焦点.
当M点在顶点位置时,M点到直线I的距离为1,故此时F点应为(2,1).
下证明M在抛物线任意位置,均有点M到直线I的距离与点M到点F的距离相等.
证明同上题,设点坐标表示出这两个距离,即可得相等.
自行证明.
(2018张家界)
如图,已知二次函数yax21(a0,a为实数)的图像过点A2,2),一次函数
ykxb(k0,k、b为实数)的图像I经过点B(0,2).
(1)求a值并写出二次函数表达式;
(2)求b值;
(3)设直线I与二次函数图像交于M,N两点,过M作MC垂直x轴于点C,试证明:
MBMC;
(4)在(3)的条件下,请判断以线段MN为直径的圆与x轴的位置关系,并说明理由.
C
则MB=
化简得MB
-m
12m
12—
12彳
-m10
又MC
一m21,
•••MB=MC.
(4)相切
过点N作ND丄x轴交x轴于点D,由(3)可得NB=ND,取MN中点P,过点P作PQ丄x轴于点Q,
111
则PQ-DNCM-BNBM-MN,
222
若以MN为直径作圆,则P点为圆心,又PQ-MN,
•••以MN为直径的圆与x轴相切.
112
C1)a一,二次函数表达式:
y—X1;
(2)b=2;
(3)由问题可推测B点即抛物线焦点,x轴是抛物线准线.
设M点坐标为m,—m1,
1:
m12
(2015•永州)
已知抛物线yax2bxc的顶点为(1,0),与y轴的交点坐标为0,--R(1,1)是
抛物线对称轴I上的一点.
(1)求抛物线yax2bxc的解析式;
(2)若P是抛物线上的一个动点(如图一),求证:
点P到R的距离与点P到直线y1的距离恒相等;
(3)设直线PR与抛物线的另一交点为Q,E为线段PQ的中点,过点P、E、Q分别作直线y1的垂线.垂足分别为M、F、N(如图二).求证:
PFQF.
x=1
*y
图1
(1)解析式:
(2)这个证明跟前面一样一样的,表示出两个距离,就能得到相等了.
设P点坐标为
m,lm12
则PR
Jm1
-m11,
1,
•••PR=PM.
(3)这个问题呢,我们换个说法:
如图,在直角梯形
ABCD中,AD//BC,/A=90。
,且CD=AD+BC,E点为AB边
中点,连接EC、ED,求证:
EC丄ED.
考虑到E点为AB边中点,倍长中线.延长DE与CB的延长线交于点F,
易证△AEDBEF,•AD=BF,
•CF=CB+BF=CB+AD=CD,易证△CED心CEF(SSS),
•••/CED=90°
•CE丄DE.
对于本题,就同理可证PF丄QF了吧.
l于R,CS
于S,连接FR、
(2015•资阳删减)
已知直线ykxb(k0)过点F(0,1),与抛物线ylx2相交于B、C两点.
(1)如图1,当点C的横坐标为1时,求直线BC的解析式;
(2)如图2,设B(m,n)(m<
0),过点E(0,-1)的直线I//x轴,BR
(1)由题意得点C坐标为1,1,故直线BC解析式为
(2)△RFS是直角三角形.
不妨把问题单独拿出来看:
E是CD边一点且满足DA=DE,
如图,在直角梯形ABCD中,AD//BC,/A=90
CB=CE,连接
AE、BE,求证:
AE丄BE.
180,
•/DA=DE
•/CB=CE
AEB
DEA
90
2,
CEB
90-
180
•••AE丄BE.
类似可证明本题中的△
RFS是直角三角形.
21
已知抛物线yax1-经过点A(0,1),AB//x轴交抛物线于B,M为线段AB的中
点,点P为抛物线上任意一点,点P的纵坐标为n.
(1)直接写出a;
线段PM的长为.(用n的代数式表示)
(2)P不为抛物线的顶点.
如图1,作PN丄x轴于N,C为x轴上一点,当△MPNABC时,求n的值;
如图2,延长PM交抛物线于Q,请证明:
—
QM
x
(1)a—,线段PM的长=n;
虽然题目并没有说M点是什么,但根据图中所画,大胆猜测:
以下检验PM=PN是否恒成立:
—21
设P点坐标为m,—m1-,又M点坐标为(1,1),
22
•2
…PM,m1
又PN=1m1
•••对于抛物线上的任意点
P均满足
所以PM的长=PN=n.
PM=PN,猜想成立.
f2
一m1
一
V2
(2)对于△PMN来说,PM=PN,即△PMN是等腰三角形,
若厶MPNABC,则△ABC必须是等腰三角形,且AB=BC.
考虑到AB=2,且点C在x轴上,不难求得
C点坐标为23,0或23,0,
F右图不是很准,意思是这个意思.
当C点坐标为23,0时,/ABC=150°
•••/MPN=15C°
•••直线PM与x轴夹角为60°
即kPM矗,
可得直线PM解析式为y•3x-31,
与抛物线联立方程:
丄x1213x11,
解得:
X131,x233,
将x,31代入直线解析式可得P点纵坐标为423,
故n的值为423.
当C点坐标为2.3,0,/ABC=30°
,则/MPN=30
•••/PMN=/PNM=75
•••/PMA=60
可得直线PM解析式为
与抛物线联立方程:
解得P点纵坐标为
2.3+4,n的值为23+4.
(3)分别过P、M、Q作x轴的垂线,垂足分别记为
qE2
G,
易证△EDMECF,
MD
FC
ED
EC
易证△CDMCEG,
GE
CD
CE
综上,n的值为4
C、D、
PC
连接EM并延长与CP延长线交于点F,连接CM并延长与EQ延长线交于点
易证△MPFMQE,可设PF=PM=PC=a,•CF=2a,
易证△MQGMPC,可设QG=QM=QE=b,•EG=2b,
CD彳
2a
2b
11
亦1
2,
即-
ab
【补充】一般地,
PCQEMD
【总结】结论1:
对于抛物线yax2,焦点坐标为0,丄,准线为直线y—.
4a4a
看前面的例子,不难发现,焦点一般会用字母F表示•而且二次项系数很多时候是1,只是
4为了焦点坐标便于计算.
至于形如yax2bxc的抛物线可化为顶点式yaxhk,然后通过由yax2平移
来确定焦点和准线.
结论2:
如下图,
证明:
设NPF
PFNQFM
90,
FM丄FN.
结论3:
取PQ中点E,作EH丄x轴交x轴于H点,贝UPH丄QH.
倍长中线证两次全等.
结论4:
记MN与y轴交于点G,则
14,即