《统计学》第五章时间数列补充例题Word下载.docx

《统计学》第五章时间数列补充例题Word下载.docx

《《统计学》第五章时间数列补充例题Word下载.docx》由会员分享，可在线阅读，更多相关《《统计学》第五章时间数列补充例题Word下载.docx（27页珍藏版）》请在冰豆网上搜索。

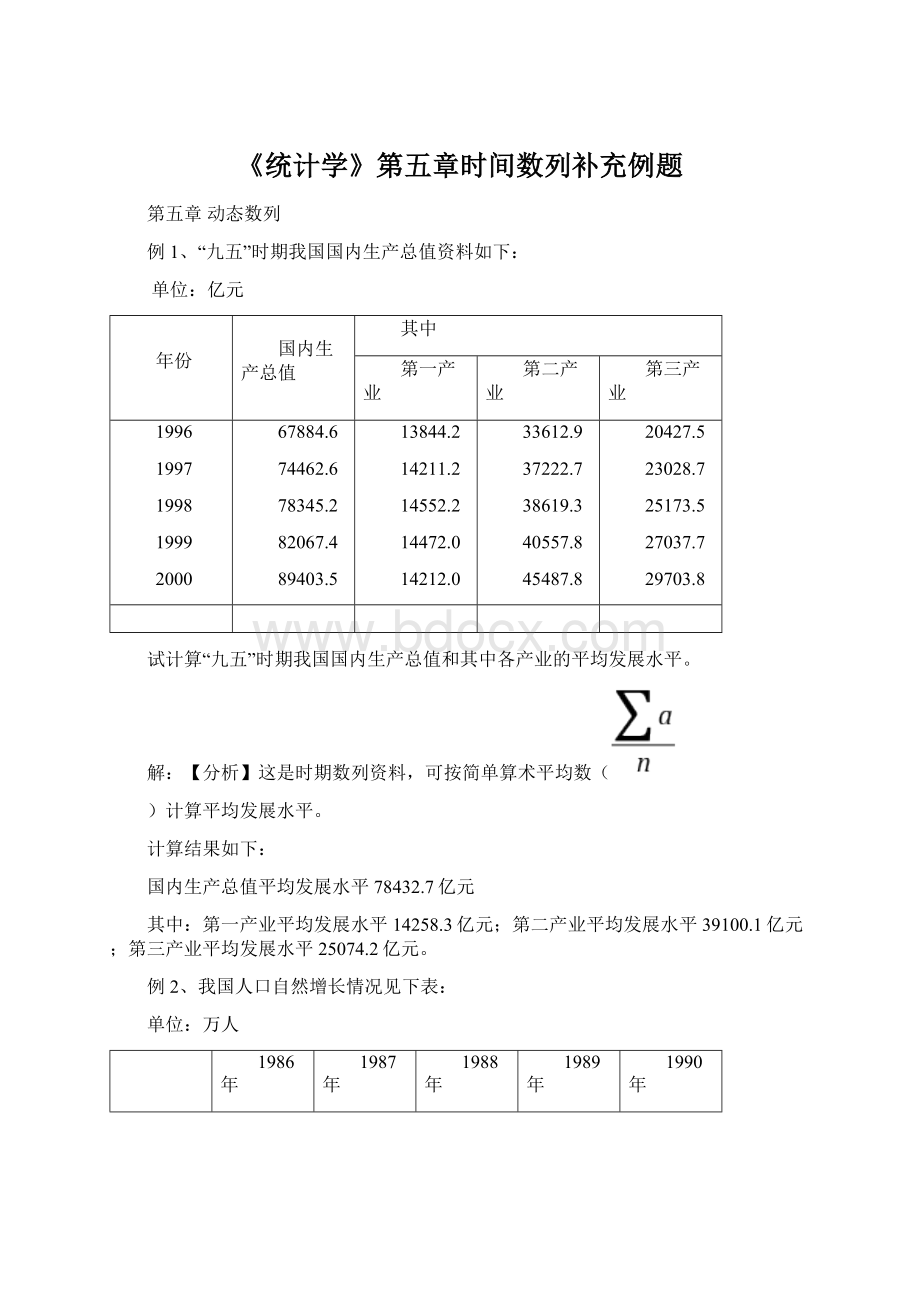
（万人）

例3、某商店2010年商品库存资料如下：

万元

日期

库存额

1月1日

1月31日

2月28日

3月31日

4月30日

5月31日

6月30日

63

60

55

48

43

40

50

7月31日

8月31日

9月30日

10月31日

11月30日

12月31日

45

57

68

试计算第一季度、第二季度、上半年、下半年和全年的平均库存额。

这是一个等间隔时点数列，用“首末折半法”计算：

例4、某企业2002年各月份记录在册的工人数如下：

2月1日

4月1日

6月1日

9月1日

12月1日

在册工人数

326

330

335

408

414

412

试计算2002年该企业平均工人数。

【分析】这是不等间隔时点数列，用间隔月数进行加权的公式计算平均工人数：

=385（人）

例5、某企业2002年各季度计划利润和利润计划完成程度的资料如下：

计划利润（万元）

利润计划完成（%）

第一季度

第二季度

第三季度

第四季度

860

887

875

898

130

135

138

125

试计算该企业年度利润计划平均完成百分比。

【分析】应该按两个时期数列对比组成的相对指标动态数列计算序时平均数的算式计算：

该企业利润年平均计划完成百分比（%）

例6、1995-2000年各年底某企业职工工人数和工程技术人员数资料如下：

职工人数

工程技术人员

1995

1000

1020

1085

1120

1218

1425

52

78

82

试计算工程技术人员占全部职工人数的平均比重。

【分析】这是由两个时点数列对比所组成的相对指标动态数列计算序时平均数的问题。

分子和分母均应按“首末折半法”计算序时平均数后加以对比。

工程技术人员占全部职工工人数比重（%）

=

例7、某工厂2003年上半年工人数和工业总产值资料如下：

月份

月初工人数（人）

总产值（亿元）

1

2

3

4

5

6

1850

2050

1950

2150

2216

2190

2.50

2.72

2.71

3.23

3.74

3.73

另外，7月初工人数为2250人。

根据上述资料计算：

（1）上半年平均工人数。

（2）上半年平均总产值。

（3）上半年平均劳动生产率。

（4）上半年劳动生产率。

【分析】解答本题要明确劳动生产率的概念；

认识月初工人数是时点指标，总产值是时期指标，然后采用相应的方法计算序时平均数加以对比。

（1）上半年平均工人数

（2）上半年平均总产值

（3）上半年平均劳动生产率

（4）上半年劳动生产率

例8、某公司的两个企业2004年2月份工业增加值及每日工人在册资料如下：

企业

增加值（万元）

工人数

1-15日

16-20日

21-28日

甲

乙

415

452

332

312

314

245

328

试计算各企业和综合两企业的月劳动生产率

先按

公式计算平均工人数

甲企业：

乙企业：

全公司：

计算结果如下表：

平均工人数（人）

月劳动生产率（元/人）

（1）

（2）

（3）=

（1）÷

302.5

327.6

13719

13797

合计

867

630

13762

例9、试利用动态指标的互相联系来确定某市生产总值动态数列水平和所缺的环比动态指标：

生产

总值

（亿元）

环比动态指标

增长量

发展速度（%）

增长速度（%）

增长1%绝对值（亿元）

353

2001

24

2002

106.1

2003

7.25

2004

2005

32

4.59

2006

108

2007

42

2008

612

5.72

2009

【分析】动态分析指标中增长速度与发展水平、前期水平与增长1%绝对值的关系是解答本题的依据。

就是结果如下表所示：

——

377

106.8

6.8

3.53

400

23

6.1

3.77

429

29

107.25

4.00

459

30

107.0

7.0

4.29

491

530

39

8.0

4.91

572

107.9

7.9

5.30

660

107.8

7.8

6.12

平均增长量=

平均发展速度=

平均增长速度=1.072-1=0.072

即该市生产总值年平均总值34.11亿元，平均发展速度107.2%。

例10、已知某公司所属甲、乙两工厂2001年利税各为500万元与1000万元，其环比增长速度如下：

%

2002年

2003年

甲厂

乙厂

12.5

10.0

10

15

试通过计算确定哪个工厂平均增长速度较高？

整个公司哪年的发展速度较快？

各年份利税总量指标计算如下：

2001年

500

500×

1.125=562.5

1000×

1.1=1100

562.5×

1.1=618.75

1100×

1.15=1265

1500

1662.5

1883.75

平均增长速度：

甲厂：

乙厂：

乙厂的平均增长速度比甲厂高1.23个百分点

公司发展速度：

2002年：

2003年：

说明整个公司2003年发展速度较快。

例11、某地区粮食产量1985—1987年平均发展速度是1.03，1988—1989年平均发展速度是1.05，1990年比1989年增长6%，试求1985—1990年六年的平均发展速度。

【分析】本题的基年是1984年，前后跨度七年，可理解为对6项环比发展速度按几何平均法计算其平均值。

平均发展速度

例12、1995年我国国内生产总值5.76万亿元。

“九五”的奋斗目标是到2000年增加到9.5万亿元，远景目标是2010年比2000年翻一番。

试问：

（1）“九五”期间将有多大平均增长速度？

（2）1996—2010年（以1995年为基期）平均每年发展速度多大才能实现远景目标？

（3）2010年人口控制在14亿内，那时人均国内生产总值达到多少元？

（1）平均发展速度=

“九五”平均增长速度将达到10.52%

（2）至2010年国内生产总值将达到的规模是：

实现远景目标的平均增长速度为：

（3）2010年人均国内生产总值将达到的水平是：

例13、某煤矿采煤量如下：

产量

7

8

9

301

302

304

291

298

310

305

315

11

12

13

14

16

17

18

19

20

308

319

320

323

296

290

334

338

21

22

25

26

27

28

336

339

345

342

356

350

351

求：

（1）按五日和按旬合并煤产量，编成时间数列；

（2）按五日和按旬计算平均日产量，编成时间数列；

（3）运用移动平均法（时距扩大为四天和五天）编制时间数列。

（1）

（2）按五日和按旬计算的采煤量与按五日和按旬的平均日产量编成时间数列。

某煤矿每五日的采煤量和每五日平均每日采煤量的时间数列

吨

日期起止

煤产量

平均日产量

1-5

6-10

11-15

1496

1552

1566

299.2

310.4

313.2

16-20

21-25

26-30

1615

1685

1744

337

348.8

某煤矿每10日的采煤量和每10日平均每日采煤量的时间数列

1-10

11-20

21-30

3048

304.8

3181

318.1

3429

342.9

（3）运用移动平均法（时距扩大为四天和五天）编制时间数列:

五天移动平均：

第一个平均数为

对正第三天原值。

依次类推移动平均，得出五天移动平均数列共26项。

四天移动平均：

对着第2-3项中间。

第二个平均数为

依次类推移动平均，得出四天移动平均数列。

最后进行二项移正平均。

趋势值

五天移动平均

四天移动平均

两项移正平均

—

299.50

229.2

299.10

298.75

301.0

299.75

300.75

301.6

300.88

301.00

303.2

303.75

306.25

308.0

308.50

310.50

310.0

310.90

311.25

312.8

312.10

313.00

314.4

313.60

314.25

316.0

315.90

317.50

316.00

314.50

309.6

307.25

311.4

308.30

309.25

313.4

310.25

311.00

315.6

315.80

320.50

323.0

325.90

331.25

332.2

332.30

333.25

333

333.4

333.80

334.25

335.1

334.80

335.25

335.8

336.00

336.50

337.0

337.00

337.25

338.8

338.60

340.00

340.4

340.50

341.00

344.4

343.25

345.50

346.4

346.90

348.25

349.00

349.75

例14、某地区年粮食总产量如下表所示：

产量（万吨）

230

236

241

246

252

257

262

276

281

286

要求：

（1）试检查该地区粮食生产发展趋势是否接近于直线型的？

（2）如果是直线型，请用最小平方法配合直线趋势方程。

（3）预测第11年的粮食生产水平。

（1）列表如下：

产量y

逐期增长量

2525

从逐期增长量可以看出，各期增长量大体相同，所以变化趋势是直线型的。

（2）配合直线趋势方程如下：

时间代码

-9

-7

-5

-3

-1

81

49

-2070

-1652

-1205

-738

-252

786

1380

1967

2574

228.17

234.51

240.85

247.19

253.53

259.87

266.21

272.55

278.89

285.23

2567

1047

把上表数据代入简化了的方程组：

解得

，

则配合的直线方程为

（3）预测第11年（

）粮食产量为：

例15、以下是某厂的单位产品成本和配合方程的相关数据：

金额（元）

环比速度（%）

435

422

407

395

382

370

97.01

96.45

97.05

96.71

96.86

36

2.6385

2.6253

2.6096

2.5966

2.5821

2.5682

5.2506

7.8288

10.3864

12.9105

15.4092

91

15.6203

54.424

预测2001年的单位产品水平。

【分析】从以上资料可知环比速度大体相同，所以其发展趋势是指数曲线型的，方程式为

设

下面用最小二乘法配合曲线方程。

所以

例16、某市1999——2002年各月毛衣销售量如下：

单位:

件

月平均

8000

6000

600

800

1200

5000

21000

25000

15000

9000

4000

2500

3500

8500

34000

35000

24000

1100

3200

7000

42000

48000

28000

14000

3000

900

3700

4800

8300

47000

51000

18750

2625

2225

5200

10625

36000

39754

根据上表资料按月平均法计算季节比率。

【分析】先计算出各年同月份的月平均数（即上表的“月平均”）和各年所有月份的月总平均数，然后将12个各年同月的平均数分别除以各年所有月份的月总平均数，得到12个季节比率，比率高说明是旺季，比率低说明是淡季。

通过计算，各年所有月份的平均数（月总平均数）为

=11348.25

所计算的季节比率如下表：

季节比率（%）

165.22

96.93

44.06

23.13

10.57

7.05

19.61

26.44

45.82

93.63

317.23

350.31

季节比率的具体计算：

如1月份的季节比率=

如12月份的季节比率=