期权价值敏感性希腊字母Word文档格式.docx
《期权价值敏感性希腊字母Word文档格式.docx》由会员分享,可在线阅读,更多相关《期权价值敏感性希腊字母Word文档格式.docx(18页珍藏版)》请在冰豆网上搜索。
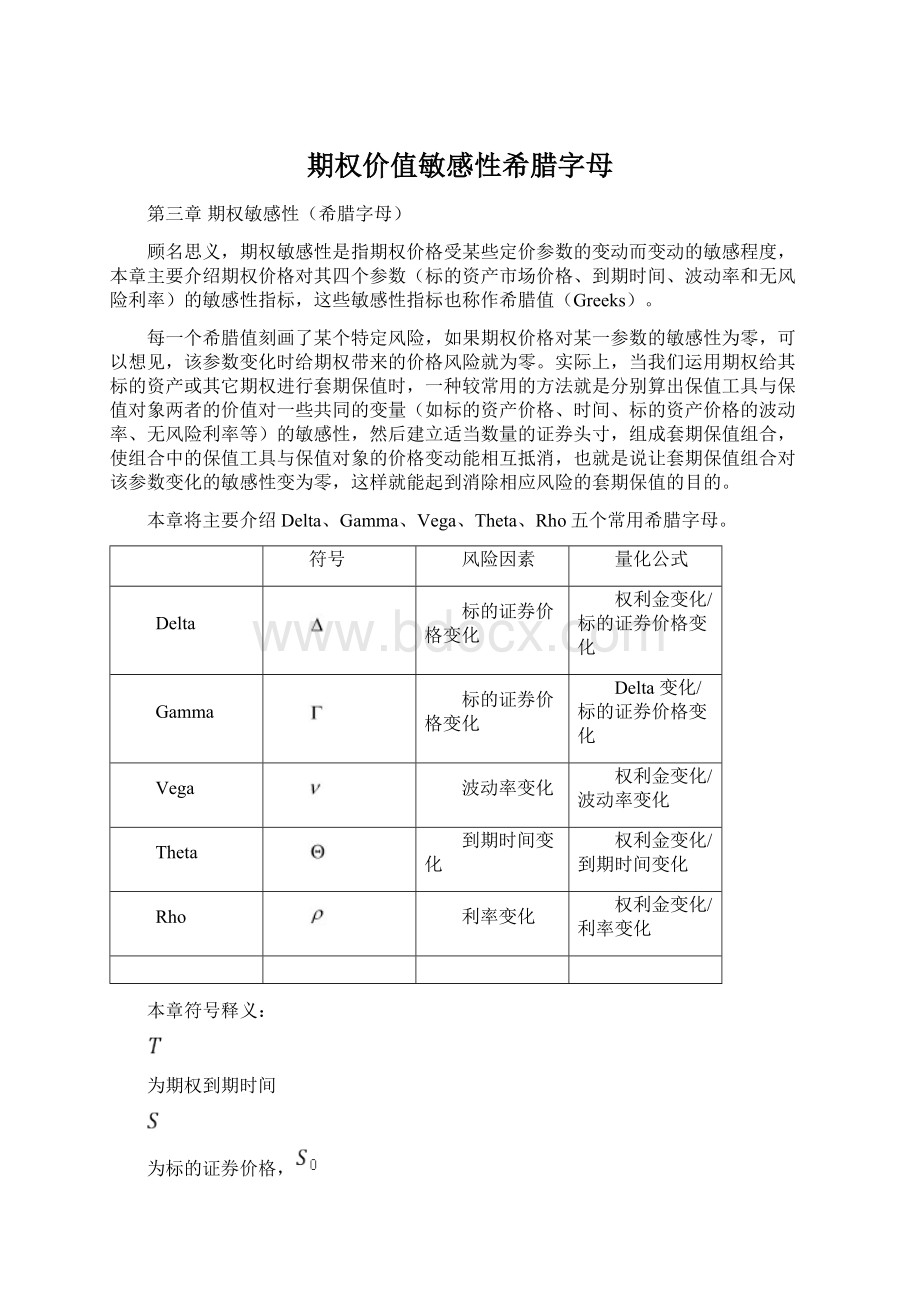
Delta衡量的是标的证券价格变化对权利金的影响,即标的证券价格变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Delta×
案例3.1有一个上证50ETF看涨期权,行权价为1.900元,期权价格为0.073元,还有6个月到期,此时上证50ETF价格为1.800元。
无风险利率为3.5%,上证50ETF波动率为20%。
Delta为0.4255。
在其他条件不变的情况下,如果上证50ETF的价格变为1.810元,即增加了0.010元,则期权理论价格将变化为:
1.2公式
从理论上,Delta准确的定义为期权价值对于标的证券价格的一阶偏导。
根据Black-Scholes期权定价公式,欧式看涨期权的Delta公式为:
(3.1)
看跌期权的Delta公式为:
(3.2)
其中
(3.3)
为标准正态分布的累积密度函数,可以查表或用计算机(如Excel)求得。
显然,看涨期权与看跌期权的Delta只差为1,这也正好与平价关系互相呼应。
案例3.2有两个行权价为1.900的上证50ETF期权,一个看涨一个看跌,离期权到期还有6个月。
此时上证50ETF价格为1.800元,无风险利率为3.5%,波动率为20%。
则:
1.3性质
1)期权的Delta取值介于-1到1之间。
也就是说标的证券价格变化的速度快于期权价值变化的速度。
2)看涨期权的Delta是正的;
看跌期权的Delta是负的。
对于看涨期权,标的证券价格上升使得期权价值上升。
对于看跌期权,标的证券价格上升使得期权价值下降。
图3-1
3)随标的价格的变化:
对于看涨期权,标的价格越高,标的价格变化对期权价值的影响越大。
对于看跌期权,标的价格越低,标的价格变化对期权价值的影响越大。
也就是说越是价内的期权,标的价格变化对期权价值的影响越大;
越是价外的期权,标的价格变化对期权价值的影响越小。
图3-2
4)Delta随到期时间的变化:
看涨期权:
价内看涨期权(标的价格>
行权价)Delta收敛于1
平价看涨期权(标的价格=行权价)Delta收敛于0.5
价外看涨期权(标的价格<
行权价)Delta收敛于0
看跌期权:
价内看跌期权(标的价格<
行权价)Delta收敛于-1
平价看跌期权(标的价格=行权价)Delta收敛于-0.5
价外看跌期权(标的价格>
图3-3
第二节Gamma(伽马,
2.1定义
在第一节里我们用Delta度量了标的证券价格变化对权利金的影响,当标的证券价格变化不大时,这种估计是有效的。
然而当标的证券价格变化较大时,仅仅使用Delta会产生较大的估计误差,此时需要引入另一个希腊字母Gamma。
Gamma衡量的是标的证券价格变化对Delta的影响,即标的证券价格变化一个单位,期权Delta相应产生的变化。
新Delta=原Delta+Gamma×
Gamma同时也间接度量了标的证券价格变化对权利金的二阶影响。
标的价格变化+1/2×
Gamma×
标的价格变化2
案例3.3有一个上证50ETF看涨期权,行权价为1.900元,期权价格为0.073元,还有6个月到期,此时上证50ETF价格为1.800元,无风险利率为3.5%,上证50ETF波动率为20%。
Delta为0.4255,Gamma为1.540。
在其他条件不变的情况下,如果上证50ETF的价格变为1.850元,即增加了0.050元,则
Delta将变化为
期权价格将变化为
2.2公式
从理论上,Gamma的定义为期权价值对于标的证券价格的二阶偏导。
Gamma衡量了Delta关于标的资产价格的敏感程度。
当Gamma比较小时,Delta变化缓慢,这时为了保证Delta中性所做的交易调整并不需要太频繁。
但是当Gamma的绝对值很大时,Delta对标的资产变动就很敏感,为了保证Delta中性,就需要频繁的调整。
根据Black-Scholes公式,对于无股息的欧式看涨与看跌期权的Gamma公式如下:
(3.4)
其中,
由式(3.3)给出,
为标准正态分布的密度函数。
在参数相同时,看涨期权、看跌期权的Gamma是相同的。
案例3.4有两个行权价为1.900元的上证50ETF期权,一个看涨一个看跌,离期权到期还有6个月。
此时上证50ETF价格为1.800元,无风险利率为3.5%,上证50ETF波动率为20%。
则
2.3性质
1)期权的Gamma是正的。
标的证券价格上涨,总是使期权的Delta变大。
图3.4
2)Gamma随标的价格的变化:
当
时,Gamma取得最大值
。
图3.5
3)Gamma随到期时间的变化:
平价期权(标的价格等于行权价)的Gamma是单调递增至无穷大的。
非平价期权的Gamma先变大后变小,随着接近到期收敛至0。
图3.6
4)Gamma随波动率的变化:
波动率和Gamma最大值呈反比,波动率增加将使行权价附近的Gamma减小,远离行权价的Gamma增加。
图3.7
第三节Vega(维嘉,
3.1定义
Vega衡量的是标的证券波动率变化对权利金的影响,即波动率变化一个单位,权利金应该产生的变化。
新权利金=原权利金+Vega
案例3.5有一个上证50ETF看涨期权,行权价为1.900元,期权价格为0.073元,还有6个月到期。
Vega为0.4989。
在其他条件不变的情况下,如果上证50ETF的波动率变为21%,即增加了1%,则期权理论价格将变化为
3.2公式
从理论上,Vega准确的定义为期权价值对于标的证券波动率的一阶偏导。
根据Black-Scholes理论进行定价,则
(3.5)
为正态分布的密度函数。
在参数相同时,看涨期权、看跌期权的Vega是相同的。
案例3.6有两个行权价为1.900元的上证50ETF期权,一个看涨一个看跌,离期权到期还有6个月。
3.3性质
1)期权的Vega是正的。
波动率增加将使得期权价值更高,波动率减少将降低期权的价值。
图3.8
2)Vega随标的价格的变化:
时,Vega取得最大值
在行权价附近,波动率对期权价值的影响最大。
图3.9
3)Vega随到期时间的变化:
Vega随期权到期变小。
期权越接近到期,波动率对期权价值的影响越小。
图3.10
第四节Theta(西塔,
4.1定义
Theta衡量的是到期时间变化对权利金的影响,即到期时间过去一个单位,权利金应该产生的变化。
新权利金=原权利金+Theta
流逝的时间
案例3.7有一个上证50ETF看涨期权,行权价为1.900元,期权价格为0.073元,还有6个月到期。
Theta为-0.1240。
在其他条件不变的情况下,如果离行权日只有5个半月了,即流逝了半个月的时间(0.0833),则期权理论价格将变化为
4.2公式
从理论上,Theta的定义为期权价值对于到期时间变化的一阶偏导。
根据Black-Sholes理论进行定价,则
(3.6)
(3.7)
案例3.8有两个行权价为1.900元的上证50ETF期权,一个看涨一个看跌,离期权到期还有6个月。
,
为标准正态分布的累积密度函数,
4.3性质
1)看涨期权的Theta是负的;
看跌期权的Theta一般为负的,但在价外严重的情况下可能为正。
因此通常情况下,越接近到期的期权Theta值越小。
图3.11
2)随标的价格的变化:
在行权价附近,Theta的绝对值最大。
也就是说在行权价附近,到期时间变化对期权价值的影响最大。
图3.12
3)Theta随到期时间的变化:
平价期权(标的价格等于行权价)的Theta是单调递减至负无穷大。
非平价期权的Theta将先变小后变大,随着接近到期收敛至0。
因此随着期权接近到期,平价期权受到的影响越来越大,而非平价期权受到的影响越来越小。
图3.13
第五节Rho(柔,
5.1定义
Rho衡量的是利率变化对权利金的影响,即利率变化一个单位,权利金相应产生的变化。
新权利金=原权利金+Rho
案例3.9有一个上证50ETF看涨期权,行权价为1.900元,期权价格为0.073元,还有6个月到期。
Rho为0.3463。
在其他条件不变的情况下,如果利率变为4.00%,即利率增加了0.50%,则期权理论价格将变化为
5.2公式
从理论上,Rho的定义为期权价值对于利率的一阶偏导。
(3.8)
(3.9)
为标准正态分布的累积密度函数。
案例3.10有两个行权价为1.900元的上证50ETF期权,一个看涨一个看跌,离期权到期还有6个月。
5.3性质
1)看涨期权的Rho是正的;
看跌期权的Rho是负的。
对于看涨期权,利率上升使得期权价值上升。
对于看跌期权,利率上升使得期权价值下降。
图3.14
Rho随标的证券价格单调递增。
对于看涨期权,标的价格越高,利率对期权价值的影响越大。
对于看跌期权,标的价格越低,利率对期权价值的影响越大。
越是价内(标的价格>
行权价)的期权,利率变化对期权价值的影响越大;
越是价外(标的价格<
行权价)的期权,利率变化对期权价值的影响越小。
图3.15
3)Rho随时间的变化:
Rho随着期权到期,单调收敛到0。
也就是说,期权越接近到期,利率变化对期权价值的影响越小。
图3.16
第六节希腊字母应用
6.1期权的希腊字母
前文中分别介绍了五个最常用的希腊字母Delta、Gamma、Vega、Theta、Rho。
影响因素
看涨期权多头
看跌期权多头
买入标的证券
标的证券价格
1
波动率
到期时间
利率
由于期权空头的价值为期权多头的负数,因此融券、期权空头的希腊字母也为股票、期权多头的负数。
看涨期权空头
看跌期权空头
融入标的证券
-1
6.2资产组合的希腊字母
案例3.11上证50ETF现价为1.800元,行权价为1.900元,六个月后到期的看涨期权,权利金为0.073元。
行权价格为1.900元,六个月后到期的看跌期权,权利金为0.140元。
构建资产组合A:
买入一手看跌期权,卖空一手看涨期权,买入10000股上证50ETF
则组合A的希腊字母如下:
组合A
一手看涨期权
一手看跌期权
10000股ETF
-4255
-5745
10000
-15398
15398
-4989
4989
653
1240
-587
-9335
-3463
-5872
组合A的成本由看涨期权多头、看跌期权空头、ETF构成
成本=10000[-0.073+0.140+1.8]=18670元
组合A的到期收益由看涨期权多头、看跌期权空头、ETF构成
组合A的价值为到期收益现值
和上面计算的希腊字母结果一致,组合A的价值不受50ETF的价格的影响,也不受波动率的影响,单受利率和到期时间的影响。
利率上升,组合A的价值将下降;
到期时间越近,组合A的价值越高。
一个同标的资产组合的希腊字母为其各个部分的希腊字母之和。
当一个资产组合的希腊字母为0,组合将不受相应市场因素的影响,损益是被锁定的,可以认为组合在这个因素上是无风险的。
6.3风险管理
五个希腊字母分别度量了标的证券的价格、标的证券波动率、期权到期时间、市场利率对期权价格的影响,是管理期权风险的主要指标。
一个资产组合在
时刻的价值,可以用下面这个公式来近似
其中主要需要考虑的是Delta、Gamma及Vega三个字母,只要管理好这些希腊字母就能有效的控制资产组合的风险。
在目前的国内市场,缺乏合适的工具来对冲Gamma和Vega,但可以利用标的现货来管理Delta。
案例3.12上证50ETF现价为1.800元,行权价为1.900元,六个月后到期的看跌期权,权利金为0.140元。
现在投资者手中持有一手看跌期权,则可计算期权的Delta为-5745。
如果投资者希望能够避免资产受上证50ETF价格变化的影响,则可以通过买入50ETF现货来中和Delta。
构建投资组合B:
一手看跌期权,买入5700股上证50ETF(股票一手为100股)。
则组合B的希腊字母如下:
组合B
5700股ETF
-45
5700
组合B的Delta为-45,组合B的成本由看跌期权多头,ETF构成
成本=100000.140+57001.800=11660元
模拟上证50ETF价格变化时,组合价值的变化
上证50ETF价格变化
组合B价值变化
不对冲Delta的情况
+0.200
+291
-850
+0.100
+75
-490
-0.100
+83
+650
-0.200
+300
+1440
对冲了Delta后,组合B受标的价格影响大大减少。
案例中提到的对冲Delta的方法成为Delta中性策略,是最常用的对冲资产组合风险的方法。
本章问题:
问
期权行情中能看到希腊字母吗?
能在交易软件上看到吗?
答:
由于希腊字母是对于期权价格变化的一种估计,没有一定的参数和计算公式,交易所不会提供相关数据。
至于在交易软件上能否看到,取决于投资者使用的软件,某些软件可能采用某种模型来计算期权的希腊字母。
为什么用书中的公式计算希腊字母,发现效果不好?
首先,希腊字母是对期权价值变化的一个度量,由于价格是有市场多空双方的供需决定的,不一定准确反映了期权价值的变化。
其二,文中使用的是Black-Scholes模型,此模型对市场有诸多修正,如无交易成本、股价符合对数正态分布等。
即使Black-Scholes公式,也不能完全准确刻画期权的价值。
因此利用文中公式计算的希腊字母,可能与实际市场中的期权价格敏感度存在差距。
希腊字母是不是绝对值越小越好?
希腊字母可以理解为期权在某一个市场因素下的风险。
诚然希腊字母绝对值越小,投资者承担的相应风险越小,但是可能的收益也越小。
收益总是伴随着风险。
通过希腊字母,投资者可以把各个方面的风险进行分解。
然后通过资产组合管理希腊字母,承受愿意承担的风险部分,对冲不愿承担的风险部分。
例如投资者判断未来股价将发生较大的变化,但不知道股价是涨或是跌,则投资者可以把资产组合的Delta和Gamma调整至0,而把Vega调高。
则投资者把自己对市场的判断体现在了投资组合上,同时回避了其他可能的风险。
希腊字母的正负号,绝对值的大小分别有什么含义?
答;
希腊字母的正负号意味着对应风险因素与期权价值变化是正相关或是负相关。
如正的Delta意味着标的价格上升会导致期权价格上升,负的Delta意味着标的价格上升会导致期权价格下降。
希腊字母的绝对值意味着期权价值对于相应风险因素的敏感度。
如Delta是1,则股价增加1元,期权价值也增加1元;
如果Delta是-0.5,则股价增加1元,期权价格减少0.5元。
一个欧式看涨期权Delta为0.3意味着什么?
如果一个投资者做空了100份看涨期权(假设一份期权对应一份股票),为了保持Delta中性,他需要买多少股票?
Delta为0.3,意味着股票价格微小变动,会导致期权价格变动相应的0.3倍,比如说,当前股价10元,股价微涨千分之一,即股价上涨了1分钱,则这时对应的期权上涨0.3分钱,同样如果股价下跌1分钱,期权下跌0.3分钱。
如果投资者做空了100份期权,那他的Delta为-0.3乘以100,及-30,由于标的股票的Delta为1,这时他需要买入30份股票,才能保证组合的Delta为0。
假如一个投资者做空了1份欧式看涨期权,他能用股票来对冲掉Gamma风险吗?
如果不能,可以采用什么办法来使Gamma中性?
投资者不能用股票来对冲Gamma,因为股票的Gamma总是0。
关于对冲Gamma,最简单的办法,他可以买入相同执行价格、相同到期日、相同标的资产的看跌期权来对冲Gamma风险。
当然也可以用相同标的资产、不同其他条款(如执行价格不同或者到期日不同)的期权,但是必须要计算出两个期权的Gamma,假设原来看涨期权的Gamma等于G0,现在用来对冲的期权的Gamma为G1,则为了是Gamma中性,他需要买入G0/G1份期权来保证Gamma中性。
为什么期权的希腊值是重要的?
期权的希腊值刻画了期权价值与市场参数的敏感程度。
期权投资者通过希腊值可以了解当市场参数变化时,期权价格的变化方向和程度。
对于进行对冲交易的投资者,可以通过希腊值确定用于对冲的期权数量,并且动态的管理对冲组合的风险。
为什么当标的资产价格在行权价附近时看涨期权Delta大约是0.5?
看涨期权Delta的数学公式是
,若直观地解释,此为最后标的资产价格在行权价之上的概率。
如果标的资产价格在行权价附近,如果假设标的资产价格随机变动,粗略的看最后有一半的概率落在行权价之上,所以其Delta大约是0.5。
为什么当标的资产价格在行权价附近时期权Delta变化最快?
即Gamma最大?
由上述Delta的概率解释,当标的资产价格在行权价附近时,有一半左右的概率最后价格落在行权价之上。
但是当资产价格大于行权价时,由于标的资产价格的随机变动的假设,最后落在行权价之上的概率会显著大于0.5;
同理当资产价格小于行权价时,最后落在行权价之上的概率会显著小于0.5。
因此当标的资产价格与行权价很接近时,此概率变化最为敏感,所以Delta的变化最快。
为何需要研究Delta的变化速率Gamma?
对于进行Delta对冲的投资者或套利者,Gamma衡量了对冲的误差。
每次进行动态对冲,买入\卖空Delta份标的资产时,一般需要持有一小段时间到下一次动态调整,这期间Delta可能变化,变化速率是Gamma,因此Gamma的大小就刻画了这期间对冲的误差。
因此整个对冲过程的误差就是把每一小段的对冲误差合在一起,也是受Gamma值所影响的。
对于平价期权为何Gamma越到期就越大?
而价外和价内期权就无此现象?
Gamma衡量的是Delta的变化速度。
当快到期时,如果标的资产价格等于行权价,则有大约一半的概率最后高于行权价;
当资产价格高于行权价,则此概率显著大于0.5(越接近到期,则概率越接近1);
当资产价格低于行权价,则此概率显著小于0.5(越接近到期,则概率越接近0)。
因此越接近到期,资产价格在行权价附近时,Delta的变动就越剧烈,所以Gamma就越大。
但是越接近到期,价外和价内的看涨期权的Delta要么接近于1,要么接近于0,变化很缓慢,因此Gamma很小。
如何理解Theta是期权价格的时间损耗?
对于看涨和看跌期权,其他参数不变,期限越长价值越高。
这点可以理解为,期限越长,标的资产价格最后越有机会落在行权价上。
并且由于可以粗略地认为标的资产价格是随机变动的,因此期限越长,最后不但高于执行价格的概率越高而且程度越大。
因此随着期限的减小,机会越来越小,最后可能高于执行价格的程度也越来越小,带来了期权价值减少。
这个变化率就是Theta的定义。
为何平价和价内或价外期权Theta相对于剩