全国中考数学试题分类汇编平面直角坐标系与点的坐标Word文档下载推荐.docx

全国中考数学试题分类汇编平面直角坐标系与点的坐标Word文档下载推荐.docx

《全国中考数学试题分类汇编平面直角坐标系与点的坐标Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《全国中考数学试题分类汇编平面直角坐标系与点的坐标Word文档下载推荐.docx（13页珍藏版）》请在冰豆网上搜索。

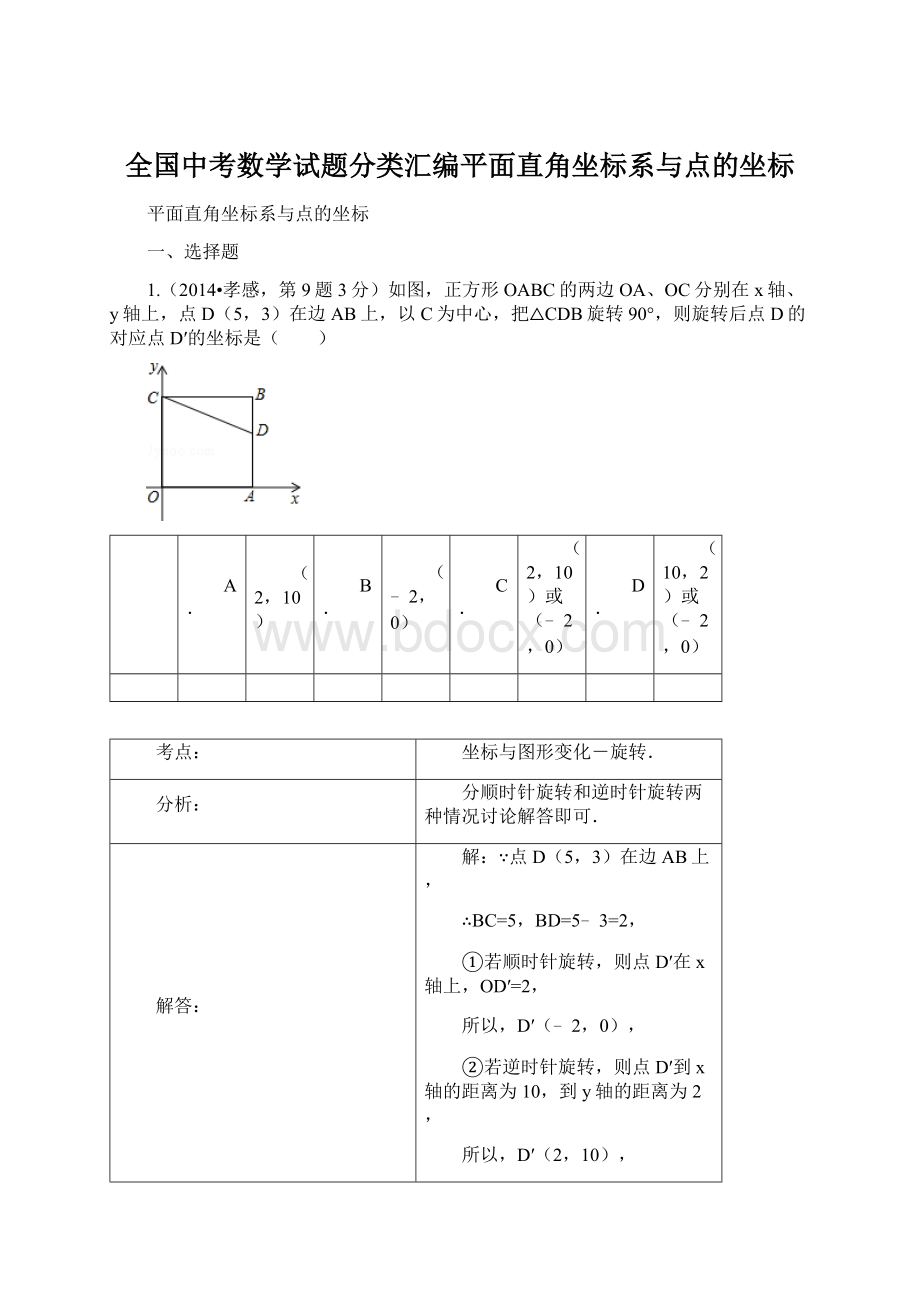
∵点D（5，3）在边AB上，

∴BC=5，BD=5﹣3=2，

①若顺时针旋转，则点D′在x轴上，OD′=2，

所以，D′（﹣2，0），

②若逆时针旋转，则点D′到x轴的距离为10，到y轴的距离为2，

所以，D′（2，10），

综上所述，点D′的坐标为（2，10）或（﹣2，0）．

故选C．

点评：

本题考查了坐标与图形变化﹣旋转，正方形的性质，难点在于分情况讨论．

2．（2014·

台湾，第9题3分）如图，坐标平面上，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB＝BC＝5．若A点的坐标为（﹣3，1），B、C两点在方程式y＝﹣3的图形上，D、E两点在y轴上，则F点到y轴的距离为何？

（　　）

A．2B．3C．4D．5

如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．由AB＝BC，△ABC≌△DEF，就可以得出△AKC≌△CHA≌△DPF，就可以得出结论．

如图，作AH、CK、FP分别垂直BC、AB、DE于H、K、P．

∴∠DPF＝∠AKC＝∠CHA＝90°

．

∵AB＝BC，

∴∠BAC＝∠BCA．

在△AKC和△CHA中。

∴△AKC≌△CHA（ASA），

∴KC＝HA．

∵B、C两点在方程式y＝﹣3的图形上，且A点的坐标为（﹣3，1），

∴AH＝4．

∴KC＝4．

∵△ABC≌△DEF，

∴∠BAC＝∠EDF，AC＝DF．

在△AKC和△DPF中，

∴△AKC≌△DPF（AAS），

∴KC＝PF＝4．

本题考查了坐标与图象的性质的运用，垂直的性质的运用，全等三角形的判定及性质的运用，等腰三角形的性质的运用，解答时证明三角形全等是关键．

3．（2014·

台湾，第13题3分）如图为小杰使用手机内的通讯软件跟小智对话的纪录．

根据图中两人的对话纪录，若下列有一种走法能从邮局出发走到小杰家，则此走法为何？

A．向北直走700公尺，再向西直走100公尺

B．向北直走100公尺，再向东直走700公尺

C．向北直走300公尺，再向西直走400公尺

D．向北直走400公尺，再向东直走300公尺

根据题意先画出图形，可得出AE＝400，AB＝CD＝300，再得出DE＝100，即可得出邮局出发走到小杰家的路径为：

向北直走AB＋AE＝700公尺，再向西直走DE＝100公尺．

依题意，OA＝OC＝400＝AE，AB＝CD＝300，

DE＝400﹣300＝100，所以邮局出发走到小杰家的路径为，

故选A．

本题考查了坐标确定位置，根据题意画出图形是解题的关键．

4.（2014•益阳，第8题，4分）如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（　　）

（第1题图）

1

1或5

3

5

直线与圆的位置关系；

坐标与图形性质．

平移分在y轴的左侧和y轴的右侧两种情况写出答案即可．

当⊙P位于y轴的左侧且与y轴相切时，平移的距离为1；

当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5．

故选B．

本题考查了直线与圆的位置关系，解题的关键是了解当圆与直线相切时，点到圆心的距离等于圆的半径．

5.（2014•株洲，第8题，3分）在平面直角坐标系中，孔明做走棋的游戏，其走法是：

棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位…依此类推，第n步的走法是：

当n能被3整除时，则向上走1个单位；

当n被3除，余数为1时，则向右走1个单位；

当n被3除，余数为2时，则向右走2个单位，当走完第100步时，棋子所处位置的坐标是（　　）

（66，34）

（67，33）

（100，33）

（99，34）

坐标确定位置；

规律型：

点的坐标

根据走法，每3步为一个循环组依次循环，且一个循环组内向右3个单位，向上1个单位，用100除以3，然后根据商和余数的情况确定出所处位置的横坐标与纵坐标即可．

由题意得，每3步为一个循环组依次循环，且一个循环组内向右3个单位，向上1个单位，

∵100÷

3=33余1，

∴走完第100步，为第34个循环组的第1步，

所处位置的横坐标为33×

3+1=100，

纵坐标为33×

1=33，

∴棋子所处位置的坐标是（100，33）．

本题考查了坐标确定位置，点的坐标的规律变化，读懂题目信息并理解每3步为一个循环组依次循环是解题的关键．

6.（2014•呼和浩特，第3题3分）已知线段CD是由线段AB平移得到的，点A（﹣1，4）的对应点为C（4，7），则点B（﹣4，﹣1）的对应点D的坐标为（　　）

（1，2）

（2，9）

（5，3）

（﹣9，﹣4）

坐标与图形变化－平移．

根据点A、C的坐标确定出平移规律，再求出点D的坐标即可．

∵点A（﹣1，4）的对应点为C（4，7），

∴平移规律为向右5个单位，向上3个单位，

∵点B（﹣4，﹣1），

∴点D的坐标为（0，2）．

本题考查了坐标与图形变化﹣平移，平移中点的变化规律是：

横坐标右移加，左移减；

纵坐标上移加，下移减．

7.（2014•菏泽，第7题3分）若点M（x，y）满足（x+y）2=x2+y2﹣2，则点M所在象限是（）

　A．第一象限或第三象限B．第二象限或第四象限

　C．第一象限或第二象限D．不能确定

点的坐标；

完全平方公式．

利用完全平方公式展开得到xy=﹣1，再根据异号得负判断出x、y异号，然后根据各象限内点的坐标特征解答．

∵（x+y）2=x2+2xy+y2，

∴原式可化为xy=﹣1，

∴x、y异号，

∴点M（x，y）在第二象限或第四象限．

本题考查了点的坐标，求出x、y异号是解题的关键，四个象限的符号特点分别是：

第一象限（+，+）；

第二象限（﹣，+）；

第三象限（﹣，﹣）；

第四象限（+，﹣）．

8.（2014•济宁，第9题3分）如图，将△ABC绕点C（0，1）旋转180°

得到△A′B′C，设点A的坐标为（a，b），则点A′的坐标为（　　）

（﹣a，﹣b）

（﹣a，﹣b﹣1）

（﹣a，﹣b+1）

（﹣a，﹣b+2）

设点A′的坐标是（x，y），根据旋转变换的对应点关于旋转中心对称，再根据中点公式列式求解即可．

根据题意，点A、A′关于点C对称，

设点A′的坐标是（x，y），

则

=0，

=1，

解得x=﹣a，y=﹣b+2，

∴点A的坐标是（﹣a，﹣b+2）．

故选：

本题考查了利用旋转进行坐标与图形的变化，根据旋转的性质得出点A、A′关于点C成中心对称是解题的关键，还需注意中点公式的利用，也是容易出错的地方．

二.填空题

1.（2014•广西玉林市、防城港市，第14题3分）在平面直角坐标系中，点（﹣4，4）在第　二　象限．

点的坐标．

根据各象限内点的坐标特征解答．

点（﹣4，4）在第二象限．

故答案为：

二．

本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：

2.（2014•邵阳，第16题3分）如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°

至OA′，则点A′的坐标是（﹣4，3）．

坐标与图形变化－旋转

过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，根据旋转的性质可得OA=OA′，利用同角的余角相等求出∠OAB=∠A′OB′，然后利用“角角边”证明△AOB和△OA′B′全等，根据全等三角形对应边相等可得OB′=AB，A′B′=OB，然后写出点A′的坐标即可．

如图，过点A作AB⊥x轴于B，过点A′作A′B′⊥x轴于B′，

∵OA绕坐标原点O逆时针旋转90°

至OA′，

∴OA=OA′，∠AOA′=90°

，

∵∠A′OB′+∠AOB=90°

，∠AOB+∠OAB=90°

∴∠OAB=∠A′OB′，

在△AOB和△OA′B′中，

∴△AOB≌△OA′B′（AAS），

∴OB′=AB=4，A′B′=OB=3，

∴点A′的坐标为（﹣4，3）．

（﹣4，3）．

本题考查了坐标与图形变化﹣旋转，熟记性质并作辅助线构造出全等三角形是解题的关键，也是本题的难点．

3.（2014·

云南昆明，第12题3分）如图，在平面直角坐标系中，点A坐标为（1，3），将线段OA向左平移2个单位长度，得到线段O′A′，则点A的对应点A′的坐标为.

作图－平移变换，平面直角坐标系点的坐标．

根据网格结构找出OA平移后的对应点O′、A′的位置，然后连接，写出平面直角坐标系中A′的坐标即可．

如图当线段OA向左平移2个单位长度后得到线段O′A′，A′的坐标为

故填

本题考查了利用平移变换作图，熟练掌握网格结构，准确找出对应点的位置是解题的关键．

4.（2014•泰州，第8题，3分）点A（﹣2，3）关于x轴的对称点A′的坐标为　（﹣2，﹣3）　．

关于x轴、y轴对称的点的坐标

让点A的横坐标不变，纵坐标互为相反数即可得到点A关于x轴的对称点A′的坐标．

∵点A（﹣2，3）关于x轴的对称点A′，

∴点A′的横坐标不变，为﹣2；

纵坐标为﹣3，

∴点A关于x轴的对称点A′的坐标为（﹣2，﹣3）．

（﹣2，﹣3）．

此题主要考查了关于x轴对称点的性质，用到的知识点为：

两点关于x轴对称，横纵坐标不变，纵坐标互为相反数．

三.解答题

1.（2014•湘潭，第17题）在边长为1的小正方形网格中，△AOB的顶点均在格点上，

（1）B点关于y轴的对称点坐标为　（﹣3，2）　；

（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；

（3）在

（2）的条件下，A1的坐标为　（﹣2，3）　．

作图－平移变换；

关于x轴、y轴对称的点的坐标．

（1）根据关于y轴对称的点的横坐标互为相反数，纵坐标相等解答；

（2）根据网格结构找出点A、O、B向左平移后的对应点A1、O1、B1的位置，然后顺次连接即可；

（3）根据平面直角坐标系写出坐标即可．

（1）B点关于y轴的对称点坐标为（﹣3，2）；

（2）△A1O1B1如图所示；

（3）A1的坐标为（﹣2，3）．

（1）（﹣3，2）；

（3）（﹣2，3）．

本题考查了利用平移变换作图，关于y轴对称点的坐标，熟练掌握网格结构准确找出对应点的位置是解题的关键．

浙江金华，第19题6分）在棋盘中建立如图所示的直角坐标系，三颗棋子A，O，B的位置如图，它们的坐标分别是

，（0，0），（1，0）.

（1）如图2，添加棋C子，使四颗棋子A，O，B，C成为一个轴对称图形，请在图中画出该图形的对称轴；

（2）在其他格点位置添加一颗棋子P，使四颗棋子A，O，B，P成为轴对称图形，请直接写出棋子P的位置的坐标.（写出2个即可）