学习球体容易出现的问题及对策Word下载.docx

学习球体容易出现的问题及对策Word下载.docx

《学习球体容易出现的问题及对策Word下载.docx》由会员分享，可在线阅读，更多相关《学习球体容易出现的问题及对策Word下载.docx（12页珍藏版）》请在冰豆网上搜索。

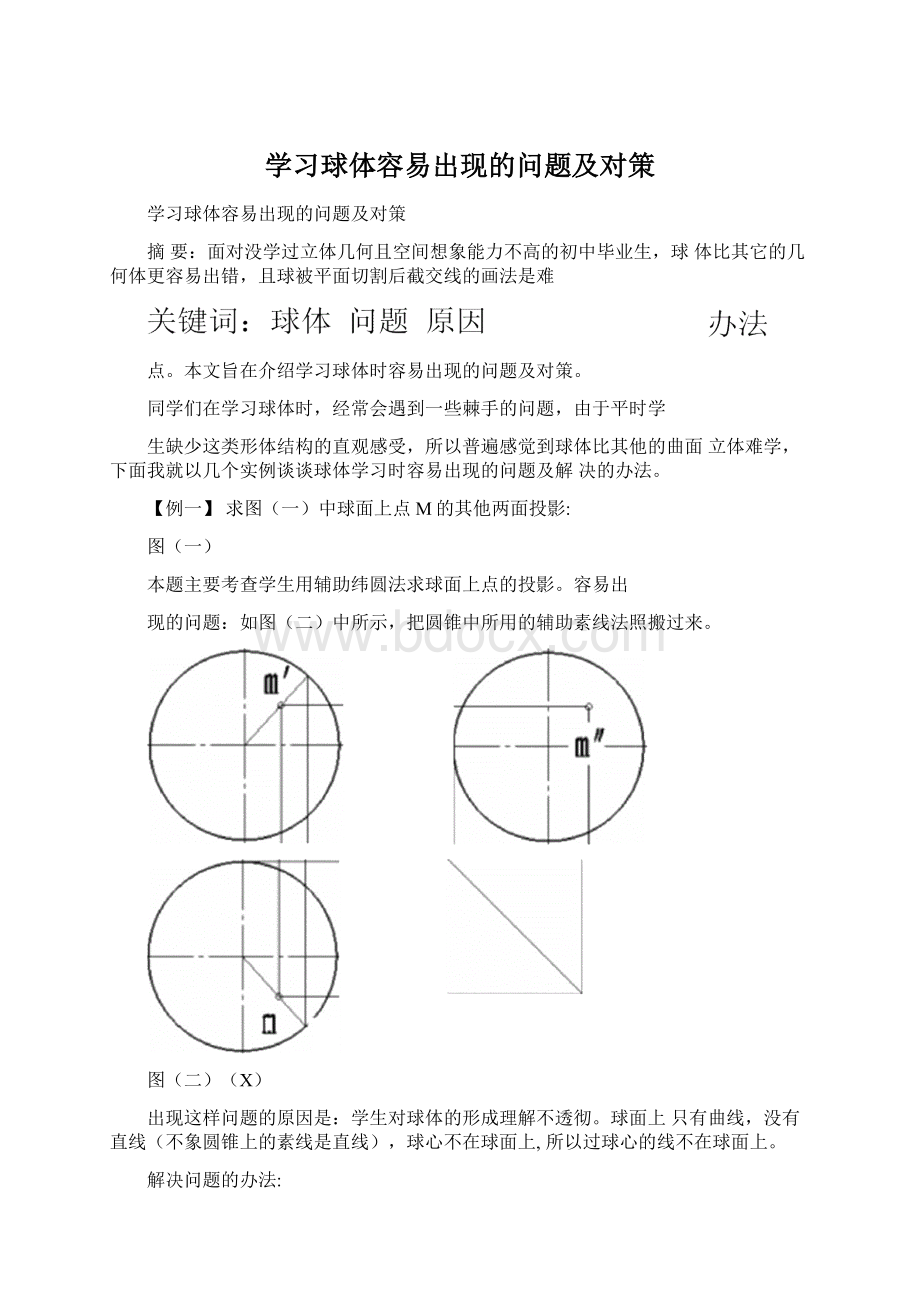
本题主要考查学生用辅助纬圆法求球面上点的投影。

容易出

现的问题：

如图

（二）中所示，把圆锥中所用的辅助素线法照搬过来。

图

（二）（X）

出现这样问题的原因是：

学生对球体的形成理解不透彻。

球面上只有曲线，没有直线（不象圆锥上的素线是直线），球心不在球面上,所以过球心的线不在球面上。

解决问题的办法:

1把球体的形成理解透彻。

球体可以看作是一个平面圆形绕其直径旋转而成的几何体。

其三面投影都是圆，直径与球直径相等，但三个投影面上的圆是球面上三

个不同方向最大轮廓的投影，正面投影是平行于V面的最大圆的投

影，水平投影是平行于H面的最大圆的投影，侧面投影是平行于W

面的最大圆的投影，如图（三）。

2、用辅助纬圆法求球面上点的投影，如图（四）所示。

由点M的正

面投影可知，点在球的上半部、右半部且正面投影可见，故在前半球,

所以其水平投影可见，侧面投影不可见。

图（四）（“）

【例二】求图（五）中球面上线的投影。

容易出现的问题：

往往凭感性认识主观地将其想象为空间直线,

找出直线两端点的两面投影，然后分别连接同面投影即成，如图（六）。

图（六）（X）

出现这样问题的原因也是对球体的理解不够透彻。

需要进行如下分析:

1、立体的特点：

平面立体各面投影由其顶点和棱线组成，各线框均

表示平面。

曲面立体中各线框则不然，有的为平面，有的为曲面，球体中只有曲面。

2、线段的特点：

平面立体表面的线段投影只可能由直线段形成；

曲

面立体表面的线段投影则可能由直线段或曲线段形成，而球体表面线段的投影只能由曲线段形成。

3、解题方法的确定：

平面立体上的线段只须找出线段两端点的投影,

然后同面投影连线即可；

球面上线段的投影要用辅助纬圆法求出各点的投影再由同面投影光滑连接而成，还要注意要判别其可见性，正确

的解法如图

【例三】补全图（八）中截交线的投影。

无论平面对对球面的相对位置如何，其截交线只有一种形状圆。

平面距离球心愈近，则交线圆的直径愈大。

根据平面对投影面的相对位置不同，截交线的投影可以是圆、直线段或椭圆。

截交线所在圆的圆心和半径不会确定。

1、这个平面是什么面，投影特性如何?

2、截交线在哪个面上投影反映实形？

再由三等关系确定圆心和

半径。

此例中，一个半球被两个侧平面和一个水平面所截，这三个面的投影特性都是一面两线，圆心及半径确定如图（九）所示，最后擦掉辅助线得到完整的三视图如图（十）所示。

图（十一）

本题主要考查学生相贯线的特殊情况。

两回转体具有公共轴线时,相贯线为垂直于该轴线的圆。

把前面学的两圆柱相贯时相贯线的画法照搬过

图（十二）（X）

1、两曲面立体的相贯线一般为空间曲线，特殊情况下是平面曲线

或直线。

2、两回转体具有公共轴线时，相贯线为垂直于该轴线的圆。

此例中，相贯线是一个侧平圆，在正面上的投影聚为线，如图（十三）

如果我们把上面的几个问题搞清楚了，那么遇到球的问题就不难解决了。

下面我们再来看一个综合例题。

【例五】

分析：

这个组合体是由四个部分组成：

上面为半球I,下面是圆

柱体皿，左边是圆柱体n；

前面为长方体W。

如图（十五）所示。

图（十五）

我们把每两个相关部分来一一进行分析，就能补全所缺的线。

第一步：

求出上半球I与左边圆柱体n的相贯线。

因为它们都是回转体，并且同轴线，所以相贯线是垂直于轴线的圆，在这里是侧平

半圆，正面投影和水平投影都聚为线，如图（十六）所示。

第二步：

求出左边圆柱体n与下面圆柱体m的相贯线。

可用简化画法,如图（十七）所示。

第三步：

求出前面长方体W与半球I的相贯线及与下面圆柱体m的交

线，如图（十八）所示。

图（十八）

最后，擦掉辅助线，得到完整的三视图，如图（十九）所示。

我们从前面的几个例题可知，学习球体这部分内容，主要是理解它的形成、投影分析，掌握球面上点、线的投影、截交线的求法及它与其他几何体的相贯线的求法，如果我们注意到上面这些问题，并能灵活运用那些对策，那么遇到球体就很容易解决了。