运动路径问题Word格式.docx

运动路径问题Word格式.docx

《运动路径问题Word格式.docx》由会员分享，可在线阅读，更多相关《运动路径问题Word格式.docx（12页珍藏版）》请在冰豆网上搜索。

，

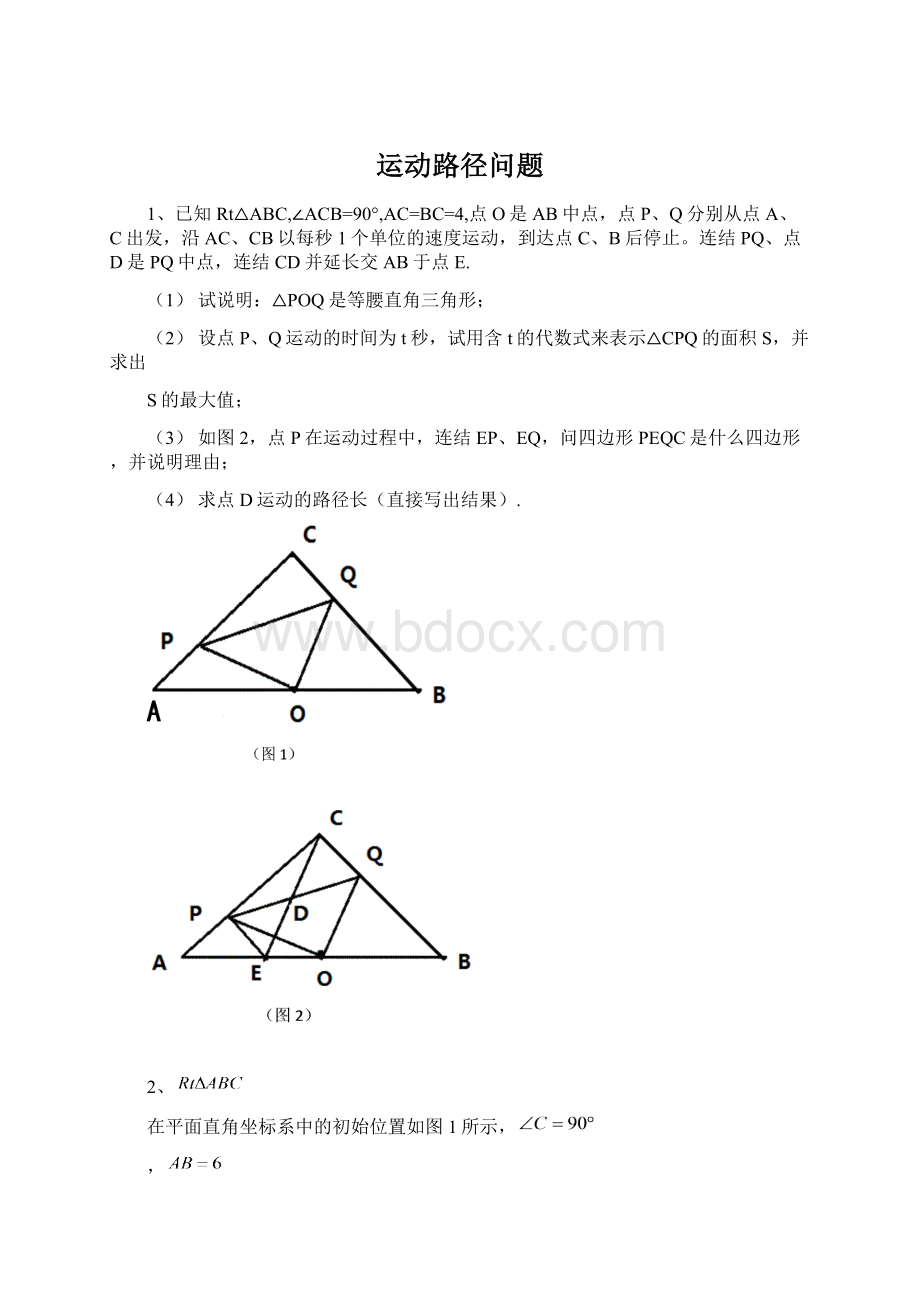
，点A在x轴上由原点O开始向右滑动，同时点B在y轴上也随之向点O滑动，如图2所示；

当点B滑动至点O重合时，运动结束。

在上述运动过程中，⊙

始终以AB为直径。

（1）试判断在运动过程中，原点O与⊙

的位置关系，并说明理由；

（2）设点C坐标为（x，y），试求出y与x的关系式，并写出自变量x的取值范围；

（3）根据对问题

（1）、

（2）的探究，请你求出整个过程中点C运动的路径的长。

3、如图①，在Rt△ABC中，

，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ，点P、Q分别从点A、C同时出发，当其上一点到达端点时，另一点也随之停止运动，设运动时间为

秒（

）

（1）直接用含

的代数式分别表示：

__________，

_____________.

（2）是否存在

的值，使四边形PDBQ为菱形，若存在，求出

的值;

若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度。

（3）如图②，在整个运动过程中，求出线段PQ中点M所经过的路径长。

如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点。

P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D。

⑴求点D的坐标（用含m的代数式表示）；

⑵当△APD是等腰三角形时，求m的值；

⑶设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2），当点P从点O向点C运动时，点H也随之运动。

请直接写出点H所经过的路径长。

（不必写解答过程）

在平面直角坐标系xOy中，点A的坐标为（0，2），直线OP经过原点，且位于一、三象限，∠AOP=45°

（如图1），设点A关于直线OP的对称点为B.

（1）写出点B的坐标；

（2）过原点O的直线l从直线OP的位置开始，绕原点O顺时针旋转，

①当直线l顺时针旋转10°

到直线l1的位置时（如图1），点A关于直线l1的对称点为C，则∠BOC的度数是，线段OC的长为；

②当直线l顺时针旋转55°

到直线l2的位置时（如图2），点A关于直线l2的对称点为D，则∠BOD的度数是；

③直线l顺时针旋转n°

（0＜n≤90），在这个运动的过程中，点A关于直线l的对称点所经过的路径长为（用含n的代数式表示）.

5.如图，一块含有30º

角的直角三角形ABC，在水平桌面上绕点C按顺时针方向旋转到A’B’C’的位置。

若BC的长为15cm，那么顶点A从开始到结束所经过的路径长为（）

A．

cmB．

cmC．

cmD．

cm

如图，一根长为2米的木棒AB斜靠在墙角处，此时BC为1米，当A点下滑至A'

处并且A'

C=1米时，木棒AB的中点P运动的路径长为米．

如图，扇形AOB中，OA=10，∠AOB=36°

．若将此扇形绕点B顺时针旋转，得一新扇形A′O′B，其中A点在O′B上，则点O的运动路径长为4π

cm．（结果保留π）

如图，在半径为4，圆心角为90°

的扇形OAB的

上有一动点P，过P作PH⊥OA于H．设△OPH的内心为I，当点P在

上从点A运动到点B时，内心I所经过的路径长为___________．

如图：

已知AB=10，点C、D在线段AB上且AC=DB=2；

P是线段CD上的动点，分别

以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为

G；

当点P从点C运动到点D时，则点G移动路径的长是________．

如图，边长为1的正六边形在足够长的桌面上滚动（没有滑动）一周，则它的中心O点所经过的路径长为。

如图，在以O为圆心，2为半径的圆上任取一点A，过点A作AM⊥y轴于点M，AN⊥x轴于点N，点P为MN的中点，当点A沿着圆圈在第一象限内顺时针方向走完45°

弧长时，则点P走过的路径长为。

18．如图，一根木棒（AB）长为2a，斜靠在与地面（OM）垂直的墙壁（ON）上，与地面的倾斜角（∠ABO）为60°

，当木棒A端沿NO向下滑动到A′，AA′＝（

）a，则B端沿直线OM向右滑动到B′，木棒中点从P随之运动到P′所经过的路径长为________．

如图，在直角坐标系中有一块三角板GEF按图1放置，其中∠GEF=60°

，∠G=90°

，EF=4．随后三角板的点E沿y轴向点O滑动，同时点F在x轴的正半轴上也随之滑动．当点E到达点O时，停止滑动．

（1）在图2中，利用直角三角形外接圆的性质说明点O、E、G、F四点在同一个圆上，并在图2中用尺规方法作出该圆，（不写作法，保留作图痕迹）；

（2）滑动过程中直线OG的函数表达式能确定吗？

若能，请求出它的表达式；

若不能，请说明理由；

（3）求出滑动过程中点G运动的路径的总长；

（4）若将三角板GEF换成一块∠G=90°

，∠GEF=α的硬纸板，其它条件不

变，试用含α的式子表示点G运动的路径的总长．

如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°

．正△ABC的边长为1，它的一边AC在MN上，且顶点A与M重合．现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．

（1）请在所给的图中，画出顶点A在正△ABC整个翻滚过程中所经过的路线图；

（2）求正△ABC在整个翻滚过程中顶点A所经过的路径长；

（3）求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S．

如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°

得点C，点C随点P的运动而运动，连接CP、CA，过点P作PD⊥OB于点D．

（1）填空：

PD的长为（用含t的代数式表示）；

（2）求点C的坐标（用含t的代数式表示）；

（3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？

若能，求t的值．若不能，请说明理由；

（4）填空：

在点P从O向A运动的过程中，点C运动路线的长为

2

边长为2的正方形ABCD的两条对角线交于点O，把BA与CD同时分别绕点B和C逆时针方向旋转，此时正方形ABCD随之变成四边形A′BCD′，设A′C，BD′交于点O，则旋转60°

时，由点O运动到点O′所经过的路径长是

如图，在Rt△ABC中，∠ACB=90°

，BC=AC=10，CP⊥AB于P，顶点C从O点出发沿x轴正方向移动，顶点A随之从y轴正半轴上一点移动到点O为止．

（1）若点P的坐标为（m，n），求证：

m=n；

（2）若OC=6，求点P的坐标；

（3）填空：

在点C移动的过程中，点P也随之移动，则点P运动的总路径长为

如图，直线l1：

y＝kx＋b平行于直线y＝x－1，且与直线l2：

y＝mx＋

交于P（－1，0）．

（1）求直线l1、l2的解析式；

（2）直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，Bn，An，…

①求点B1，B2，A1，A2的坐标；

②请你通过归纳得出点An、Bn的坐标；

并求当动点C到达An处时，运动的总路径的长．

如图，正方形ABCD的边长是2，M是AD的中点．点E从点A出发，沿AB运动到点B

停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、

FG．

（1）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，并填写自变量x的

取值范围；

（2）P是MG的中点，请直接写出点P运动路线的长．

（1）如图1，已知点P在正三角形ABC的边BC上，以AP为边作正三角形APQ，连接CQ．

①求证：

△ABP≌△ACQ；

②若AB=6，点D是AQ的中点，直接写出当点P由点B运动到点C时，点D运动路线的长．

（2）已知，△EFG中，EF=EG=13，FG=10．如图2，把△EFG绕点E旋转到△EF'

G'

的位置，点M是边EF'

与边FG的交点，点N在边EG'

上且EN=EM，连接GN．求点E到直线GN的距离．

20-10π