现代控制理论实验报告《南理工自动化专业》Word文档格式.docx
《现代控制理论实验报告《南理工自动化专业》Word文档格式.docx》由会员分享,可在线阅读,更多相关《现代控制理论实验报告《南理工自动化专业》Word文档格式.docx(26页珍藏版)》请在冰豆网上搜索。
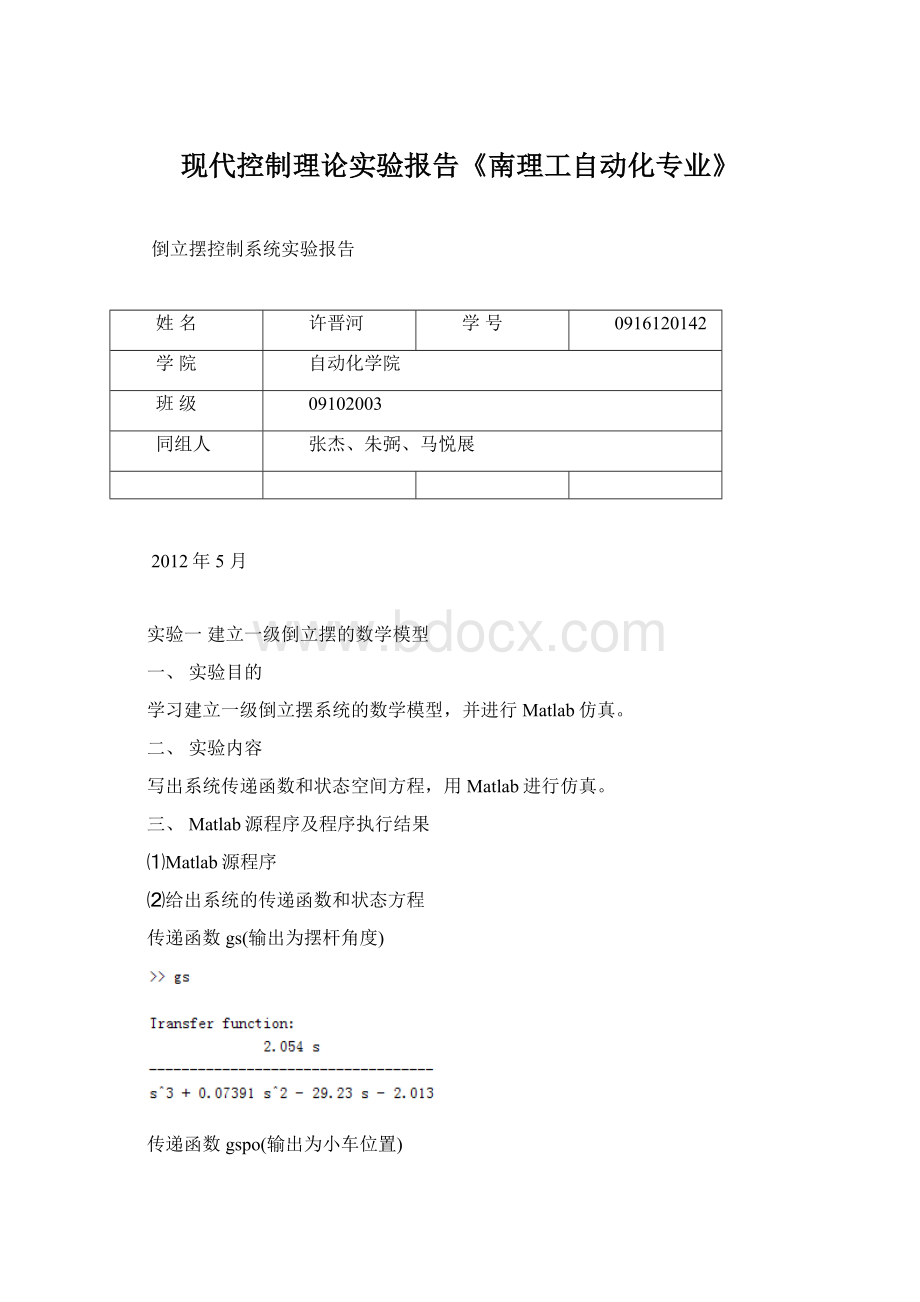
⑶给出传递函数极点和系统状态矩阵A的特征值
传递函数gs极点P
传递函数gspo极点Po
系统状态矩阵A的特征值E
⑷给出系统开环脉冲响应和阶跃响应的曲线
系统开环脉冲响应曲线
系统开环阶跃响应曲线
四、思考题
(1)由状态空间方程转化为传递函数,是否与直接计算传递函数相等?
通过比较,可知传递函数gspo由状态空间方程转化为传递函数时,多了s的一次项,但是系数可以近似为0。
传递函数gs,则完全相等。
所以,状态空间方程转化为传递函数与直接计算传递函数可以认为是相等的。
(2)通过仿真表明开环系统是否稳定?
请通过极点(特征值)理论来分析。
开环系统不稳定。
根据极点理论可知,系统稳定的条件是极点均在左半平面。
但是,系统有一个极点5.4042不在左半平面。
因此,系统不稳定
(3)传递函数的极点和状态方程的特征值的个数、大小是否相等?
如果不相等,请解释
其原因。
传递函数gspo的极点和状态方程的特征值的个数、大小相等。
但是传递函数gs的极点和状态方程的特征值个数不相等。
因为存在零极点对消。
Matlab源程序:
clearall;
f1=0.001;
%实际系统参数
M=1.32;
m=0.132;
b=0.1;
l=0.27;
I=0.0032;
g=9.8;
T=0.02;
%求传递函数gs(输出为摆杆角度)和gspo(输出为小车位置)
q=(M+m)*(I+m*l^2)-(m*l)^2;
num=[m*l/q0];
den=[1b*(I+m*l^2)/q-(M+m)*m*g*l/q-b*m*g*l/q];
gs=tf(num,den);
numpo=[(I+m*l^2)/q0-m*g*l/q];
denpo=[1b*(I+m*l^2)/q-(M+m)*m*g*l/q-b*m*g*l/q0];
gspo=tf(numpo,denpo);
%求状态空间sys(A,B,C,D)
p=I*(M+m)+M*m*l^2;
A=[0100;
0-(I+m*l^2)*b/pm^2*g*l^2/p0;
0001;
0-m*b*l/pm*g*l*(M+m)/p0];
B=[0;
(I+m*l^2)/p;
0;
m*l/p];
C=[1000;
0010];
D=[0;
0];
sys=ss(A,B,C,D);
%通过传递函数求系统(摆杆角度和小车位置)的开环脉冲响应
t=0:
T:
5;
y1=impulse(gs,t);
y2=impulse(gspo,t);
figure
(1);
plot(t,y2,'
b'
t,y1,'
r'
);
xlabel('
t/s'
ylabel('
Position/morAngle/rad'
axis([02080]);
legend('
CarPosition'
'
PendulumAngle'
%将状态空间方程sys转化为传递函数gs0
gs0=tf(sys);
%通过状态方程求系统(摆杆角度和小车位置)的开环脉冲响应
y=impulse(sys,t);
figure
(2);
plot(t,y(:
1),t,y(:
2),'
%通过传递函数求系统(摆杆角度和小车位置)的开环阶越响应
y1=step(gs,t);
y2=step(gspo,t);
figure(3);
axis([02.5080]);
%通过状态方程求系统(摆杆角度和小车位置)的开环阶越响应
y=step(sys,t);
figure(4);
%求传递函数极点
P=pole(gs);
Po=pole(gspo);
%求A的特征值
E=eig(A);
实验二倒立摆系统控制算法的状态空间法设计
学习如何使用状态空间法设计系统的控制算法。
用状态空间法设计控制器,使得当在小车上施加0.2m的阶跃信号时,闭环系统的响应指标为:
(1)杆角度µ
和小车位移x的稳定时间小于5秒
(2)x的上升时间小于2秒2
(3)µ
的超调量小于20度(0.35弧度)
(4)稳态误差小于4%.
三、Matlab源程序及程序执行结果
⑴给出Matlab程序的执行结果和仿真图形(确定K和反馈后的响应曲线);
反馈后的响应曲线
⑵给出无扰动时两次不同K值下,小车的稳定位置P1和摆杆的稳定角度Pend1;
①K=
-14.1421-12.146763.582511.8413
小车的稳定位置P1=-0.01
绿色的曲线为摆杆的稳定角度Pend1=0.002度
②K=
-14.1421-12.157063.583711.8416
小车的稳定位置P1=-0.007
绿色的曲线为摆杆的稳定角度Pend1=0.0015度
⑶给出阶跃输入时两次不同K值下,小车的稳定位置P2-P1和摆杆的稳定角度Pend2
小车的稳定位置P2-P1=0.0825-(-0.01)=0.0925
摆杆的稳定角度Pend2=0.008度
小车的稳定位置P2-P1=0.085-(-0.007)=0.092
摆杆的稳定角度Pend2=0.005度
⑷给出两次不同K值下,实际系统的响应曲线,并计算实验要求中的四项响应指标,并注意要利用实验三中统计出的响应时间延迟修正响应曲线。
=(0.11-0.0825)/0.0925=29.7%tp=(4100-3880)/1000*8.8=1.936s
tr=(4030-3880)/1000*8.8=1.32sts=(4800-3880)/1000*8.8=8.096s
=(0.11-0.085)/0.092=27.17%tp=(3025-2840)/1000*8.8=1.628s
tr=(2955-2840)/1000*8.8=1.012sts=(4800-3900)/1000*8.8=7.92s
四、思考题
(1)计算Ac的特征值。
(2)通过仿真分析Q11和Q33的大小对控制效果的影响(Q11为Q阵的第(1;
1)个元素):
•固定Q33,改变Q11
Q33=100Q11=100(红)、500(蓝)、1000(绿)
从图中可以看出Q11增大,角度超调随着增大,位置的超调基本不变,但是响应时间缩短了。
•固定Q11,改变Q33
Q11=100Q33=100(红)、1000(蓝)、2000(绿)
从图中可以看出Q33增大,角度超调减小,位置的超调基本不变,但是响应时间延长了。
%M=1.096;
%m=0.109;
%b=0.25;
%l=0.25;
%I=0.0034;
%g=9.8;
%T=0.001;
%求系统状态空间参数
b=0.22;
D=0;
%求反馈向量K
R=1;
Q1=200;
Q2=0;
Q3=100;
Q=[Q1000;
0Q200;
00Q30;
0000];
K=lqr(A,B,Q,R);
%求状态反馈后的系统sysstate
Ac=A-B*K;
Bc=B*K
(1);
%输入变换使输入与反馈的量纲匹配
sysstate=ss(Ac,Bc,C,D);
%对lqr控制系统进行仿真
U=0.2*ones(size(t));
y=lsim(sysstate,U,t);
holdon;
boxon;
实验三研究倒立摆系统对信号的跟踪
观察倒立摆对于不同输入信号的跟踪情况,加深对状态空间和状态反馈的理解。
在平衡位置,分别设定下列三种信号,记录倒立摆的运动情况:
(1)方波信号:
频率0.001Hz,幅值0.05m
(2)正弦波信号:
(3)锯齿波信号:
⑵给出Matlab的仿真图形(三种扰动下的响应曲线)
锯齿波干扰的响应曲线:
方波干扰的响应曲线:
正弦波干扰的响应曲线:
⑶给出实际系统的响应曲线
方锯齿波干扰的实际响应曲线:
波干扰的实际响应曲线:
由方波实际响应曲线可以知道时间对应关系为1000对应8.8s
时间修正后的方波曲线:
正弦波干扰的实际响应曲线:
⑷利用实验步骤(10)中的方法统计响应时延
锯齿波干扰的实际响应曲线可以得到响应时延为0.229s
⑸根据统计出的时延,对实验二中阶跃响应的曲线进行修正
修正后的曲线:
(1)仿真曲线和实际响应曲线是否大致相同?
通过比较可以看出仿真的曲线和实际响应曲线大致相同。
不过,可以看出角度的实际响应比仿真响应的超调要大些。
(2)请说明原系统是否完全可控?
因为3<
4,所以,原系统不完全可控。
五、实验研究的体会和收获
将理论课上的机理法运用于建立一级倒立摆系统的数学模型,加深了对状态空间、状态空间控制算法和状态反馈的理解。
实验中的存在的不足之处:
①在时间转换的计时过程中出现了较大的误差。
②K值是通过改变摩擦系数来改变的。
但由于担心K值变化过大导致实际系统不稳定。
最后K取值变化过小,实验结果虽然是正确的,但是效果不是很明显。
M=1.096;
m=0.109;
b=0.25;
l=0.25;
I=0.0034;
0000;
%输入变换使输入与反馈的量纲匹配
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%信号模拟发生器
T=0.02
Tmax=45;
%生成阶跃信号¨
%t=0:
Tmax;
%U=0.1*ones(size(t));
%生成方波¨
U=0.1.*gensig('
square'
15,Tmax,T)-0.1/2;
%生成正弦波
%U=0.1*sin(2*pi*t/15);
%生成正弦波波
%U=(1-mod(t/8,1)-0.5)*0.1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%