电力系统稳定性分析matlab程序文档格式.docx
《电力系统稳定性分析matlab程序文档格式.docx》由会员分享,可在线阅读,更多相关《电力系统稳定性分析matlab程序文档格式.docx(12页珍藏版)》请在冰豆网上搜索。
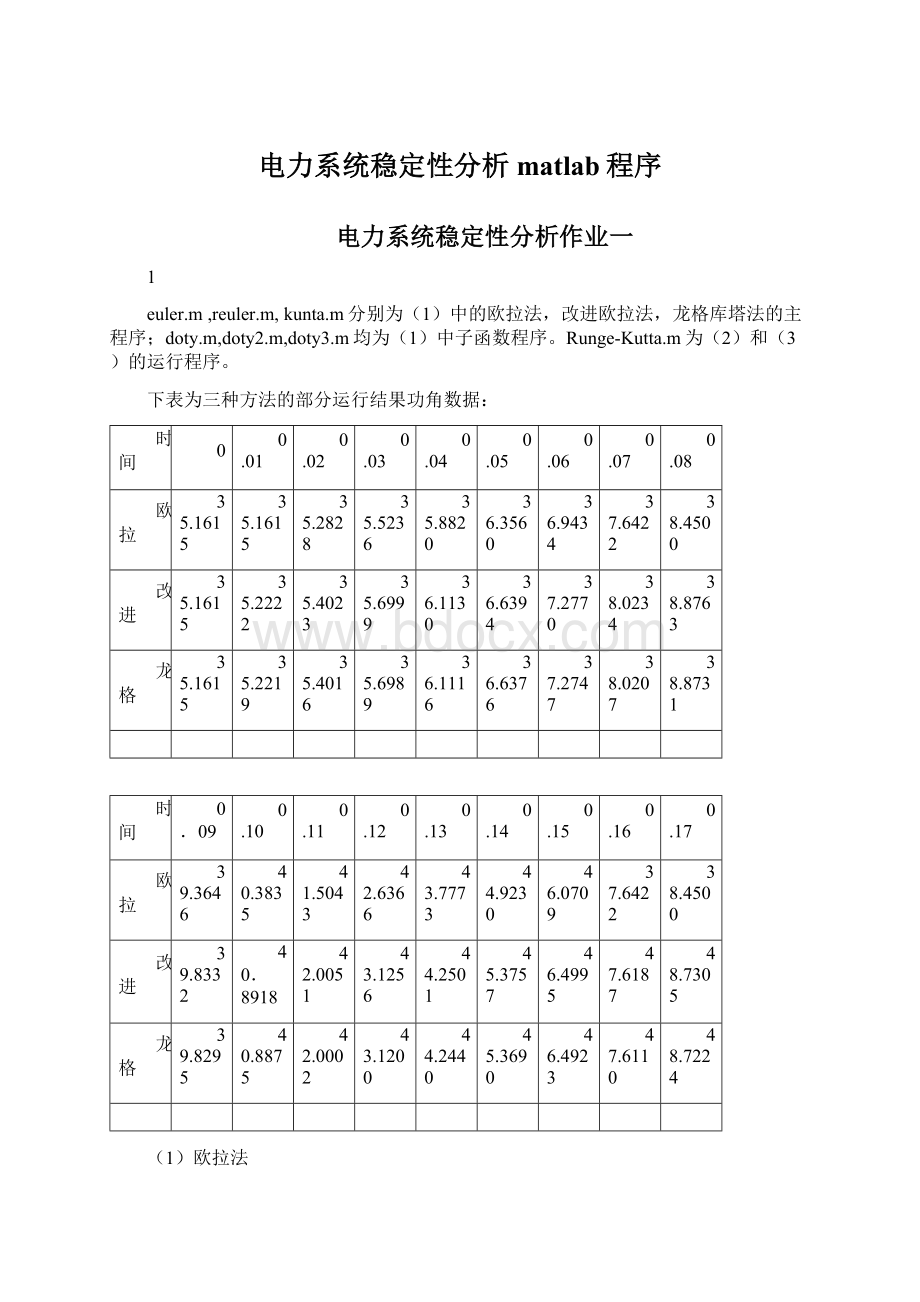
35.4023
35.6999
36.1130
36.6394
37.2770
38.0234
38.8763
龙格
35.2219
35.4016
35.6989
36.1116
36.6376
37.2747
38.0207
38.8731
0.09
0.10
0.11
0.12
0.13
0.14
0.15
0.16
0.17
39.3646
40.3835
41.5043
42.6366
43.7773
44.9230
46.0709
39.8332
40.8918
42.0051
43.1256
44.2501
45.3757
46.4995
47.6187
48.7305
39.8295
40.8875
42.0002
43.1200
44.2440
45.3690
46.4923
47.6110
48.7224
(1)欧拉法
在matlaB中输入命令[t,x,y,z]=euler('
doty'
'
doty2'
doty3'
0,5,0.1,0.01)可得
t-w曲线,t-δ曲线分别如下图所示。
具体功角,角速度数据分别见文件1.mat和2.mat
(2)欧拉改进法
在matlab命令窗口输入[t,x,y,z]=reuler('
0,5,0.1,0.01)
具体功角,角速度数据分别见文件3.mat和4.mat
(3)龙格库塔法
在matlab命令窗口输入[t,x,y,z]=kunta('
具体功角,角速度数据分别见文件5.mat和6.mat
2
运行Runge-Kutta,将参数阻尼D设置为0.05,不断更改参数切除时间t的值,当t=0.2728和t=0.2730时,运行程序分别得到如下两图:
则当阻尼D=0.05时,临界切除时间CCT=0.2729
类似可以求得:
阻尼D=0.2时,临界切除时间为CCT=0.5729
由以上数据我们可以看出:
阻尼增大时,临界切除时间也增大了。
即伴随阻尼的增大,功角和角速度振荡衰减更明显,系统更容易回到平衡状态,系统的稳定性更好。
3
接地阻抗X=0.05时,临界切除时间CCT=0.2462
接地阻抗X=0.1时,临界切除时间CCT=0.3112
接地阻抗增大时,系统临界切除时间也增大了,系统稳定性变好。
附注:
以下为详细的程序清单。
【Euler.m】欧拉法主程序
function[t,x,y,z]=euler(fun1,fun2,fun3,t0,xfinal,tm,h)
n=(xfinal-t0)/h;
n1=(tm-t0)/h;
globalKwp0pp2d1wpp1
f=50;
Tj=11;
p0=1.0;
d1=0.05;
xd=0.29;
xt1=0.13;
xt2=0.11;
xx=0.07149;
xl=0.58;
E0=1.4239;
V0=1.0;
w=2*pi*f;
Kw=w^2/Tj;
x1=xd+xt1+0.5*xl+xt2;
x2=x1+(xd+xt1)*(0.5*xl+xt2)/xx;
x3=x1+0.5*xl;
pp1=E0*V0/x2;
pp2=E0*V0/x3;
t
(1)=t0;
x
(1)=asin(p0*x1/E0/V0);
y
(1)=2*pi*f;
z
(1)=x
(1)*180/pi;
forii=1:
n1
t(ii+1)=t(ii)+h;
x(ii+1)=x(ii)+h*feval(fun1,y(ii));
y(ii+1)=y(ii)+h*feval(fun2,x(ii),y(ii));
z(ii+1)=x(ii+1)*180/pi;
end
forii=n1+1:
n
y(ii+1)=y(ii)+h*feval(fun3,x(ii),y(ii));
【reuler.m】改进欧拉法主程序:
function[t,x,y,z]=reuler(fun1,fun2,fun3,t0,xfinal,tm,h)
k1=feval(fun1,y(ii));
g1=feval(fun2,x(ii),y(ii));
x0=x(ii)+h*k1;
y0=y(ii)+h*g1;
k2=feval(fun1,y0);
g2=feval(fun2,x0,y0);
x(ii+1)=x(ii)+h/2*(k1+k2);
y(ii+1)=y(ii)+h/2*(g1+g2);
g1=feval(fun3,x(ii),y(ii));
g2=feval(fun3,x0,y0);
subplot(1,2,1)
plot(t,y)
subplot(1,2,2)
plot(t,z);
【kunta.m】龙格库塔法主程序
function[t,x,y,z]=kunta(fun1,fun2,fun3,t0,xfinal,tm,h)
x11=x(ii)+0.5*h*k1;
y11=y(ii)+0.5*h*g1;
k2=feval(fun1,y11);
g2=feval(fun2,x11,y11);
x22=x(ii)+0.5*h*k2;
y22=y(ii)+0.5*h*g2;
k3=feval(fun1,y22);
g3=feval(fun2,x22,y22);
x33=x(ii)+h*k2;
y33=y(ii)+h*g2;
k4=feval(fun1,y33);
g4=feval(fun2,x33,y33);
x(ii+1)=x(ii)+h/6*(k1+2*k2+2*k3+k4);
y(ii+1)=y(ii)+h/6*(g1+2*g2+2*g3+g4);
g2=feval(fun3,x11,y11);
g3=feval(fun3,x22,y22);
g4=feval(fun3,x33,y33);
以下为子程序【doty.m】
functionfun1=doty(y)
globalw
fun1=(y-w);
【doty2.m】
functionfun2=doty2(x,y)
globalwp0pp1d1Kw
fun2=Kw*(p0-pp1*sin(x)-d1*(y-w))/y
【doty3.m】
functionfun3=doty3(x,y)
globalKwp0pp2d1w
fun3=Kw*(p0-pp2*sin(x)-d1*(y-w))/y;
以下为四阶龙格库塔法求临界切除时间程序:
functionjj
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始值
symsE0xdTjxt1xt2xlDxzU0P0Q0;
U0=1;
P0=1;
Q0=0.2;
h=0.0001;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%²
参数调试
xdet=0.07149;
%xdet=0.07149;
D=0.05;
%D=0.05;
t=0.2730;
%xdet=0.07149;
D=0.05修改t可得到t=CCT=0.2729det_c_lim=det3(2729)
D=0.2修改t可得到t=CCT=0.5729det_c_lim=det3(5729)
%xdet=0.05;
D=0.05修改t可得到t=CCT=0.2462det_c_lim=det3(2462)
%xdet=0.1;
D=0.05修改t可得到t=CCT=0.3111det_c_lim=det3(3111)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始公式
wn=2*pi*50;
w1
(1)=wn;
w2
(1)=wn;
w3
(1)=wn;
T=t*10000;
det1
(1)=35.1615;
det2
(1)=35.1615;
det3
(1)=35.1615;
Kw=wn^2/Tj;
Xdnum1=xd+xt1+0.5*xl+xt2;
Peli1=E0*U0/Xdnum1;
Xdnum2=Xdnum1+(xd+xt1)*(0.5*xl+xt2)/xdet;
Peli2=E0*U0/Xdnum2;
Xdnum3=Xdnum1+0.5*xl;
Peli3=E0*U0/Xdnum3;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%四阶龙格库塔
当t<
0.1s时,故障
fori=1:
T
K1det(i)=(w3(i)-wn)*180/pi;
Pd=D*(w3(i)-wn);
K1w(i)=Kw*(P0-Pd-Peli2*sin(det3(i)*2*pi/360))/w3(i);
det_c0=det3(i)+0.5*h*K1det(i);
w_c0=w3(i)+0.5*h*K1w(i);
K2det(i)=(w_c0-wn)*180/pi;
Pd=D*(w_c0-wn);
K2w(i)=Kw*(P0-Pd-Peli2*sin(det_c0*2*pi/360))/w_c0;
det_c1=det3(i)+0.5*h*K2det(i);
w_c1=w3(i)+0.5*h*K2w(i);
K3det(i)=(w_c1-wn)*180/pi;
Pd=D*(w_c1-wn);
K3w(i)=Kw*(P0-Pd-Peli2*sin(det_c1*2*pi/360))/w_c1;
det_c2=det3(i)+h*K3det(i);
w_c2=w3(i)+h*K3w(i);
K4det(i)=(w_c2-wn)*180/pi;
Pd=D*(w_c2-wn);
K4w(i)=Kw*(P0-Pd-Peli2*sin(det_c2*2*pi/360))/w_c2;
det3(i+1)=det3(i)+h*(K1det(i)+2*K2det(i)+2*K3det(i)+K4det(i))/6;
w3(i+1)=w3(i)+h*(K1w(i)+2*K2w(i)+2*K3w(i)+K4w(i))/6;
%t>
0.1s后清除故障
fori=T+1:
50000
K1w(i)=Kw*(P0-Pd-Peli3*sin(det3(i)*2*pi/360))/w3(i);
K2w(i)=Kw*(P0-Pd-Peli3*sin(det_c0*2*pi/360))/w_c0;
K3w(i)=Kw*(P0-Pd-Peli3*sin(det_c1*2*pi/360))/w_c1;
K4w(i)=Kw*(P0-Pd-Peli3*sin(det_c2*2*pi/360))/w_c2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%显示数据及图形
t=0:
0.0001:
5;
plot(t,det3(),'
b'
);
%t=0:
plot(t,w3(),'
Welcome!
!
欢迎您的下载,
资料仅供参考!