实验动物剂量换算问题的解析Word格式文档下载.docx

实验动物剂量换算问题的解析Word格式文档下载.docx

《实验动物剂量换算问题的解析Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《实验动物剂量换算问题的解析Word格式文档下载.docx（15页珍藏版）》请在冰豆网上搜索。

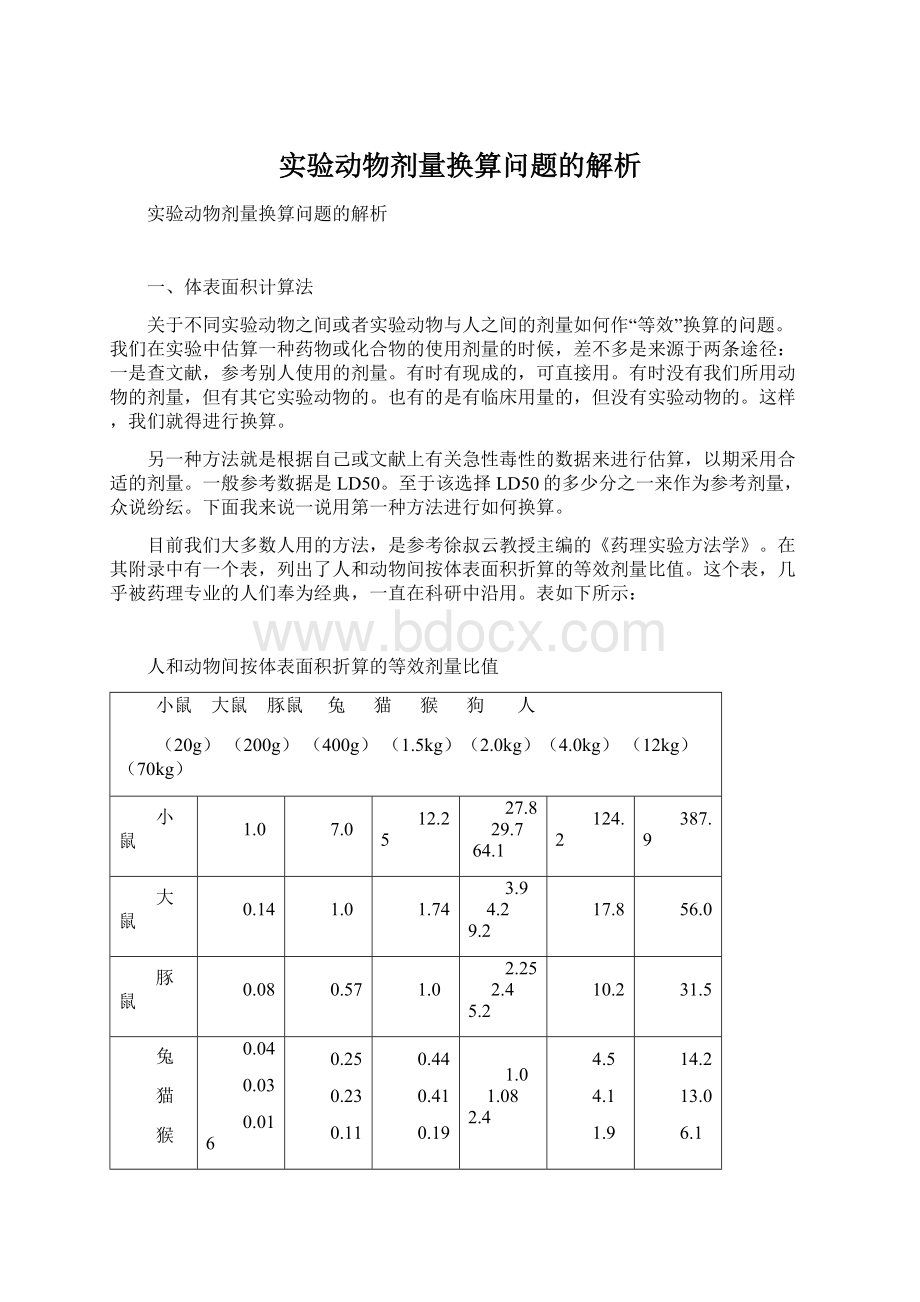
兔

猫

猴

0.04

0.03

0.016

0.25

0.23

0.11

0.44

0.41

0.19

1.0 

1.08 

2.4

0.92 

1.0 

2.2

0.42 

0.45 

1.0

4.5

4.1

1.9

14.2

13.0

6.1

狗

0.008

0.06

0.10

0.22 

0.23 

0.52

3.1

人

0.0026

0.018

0.031

0.07 

0.078 

0.06

0.32

本人认为在此表中，人的体重设为70kg，是有点不妥的。

如果设为60kg，则能为大多数人接受。

这样一来，这个表就得进行修正。

如果为60kg，则人的体表面积为1.55m2左右。

那么，这样一来，折算系数表的中数字，全部要修正。

最后一行的数字要乘以1.72/1.55=1.11，而表最右上端的人的体重改为60kg。

那么我们来看看上面这个表的最后一行，这个也是我们通常要用到的，把人的临床剂量转换为实验动物的剂量。

但是如果按这个表来计算实验动物的等效剂量，需要动物的体重基本上在标准体重的区间内相差不大才会准确。

也就是说，小鼠在20g左右，大鼠在200g左右，豚鼠在400g左右等等，这样计算出来才会准确。

当大鼠的体重为180g、250g、300g、350g、400g时，那么它的剂量根据体型系数计算实际体表面积应是多少？

而按折算系数算又是多少？

它们之间相差有多大？

当大鼠体重在哪个范围内波动时，上述折算系数仍然基本准确呢？

为什么说，当实验动物体重不在上述标准体重的附近的话，按折算系数算出来的剂量就不那么准了呢？

这是因为，我们用这个折算系数，只是一个点对点的关系。

就是说，70kg的人对200g的大鼠，那么这个剂量完全准确的。

但如果大鼠不是200g，那么就会有偏差了。

这个偏差来源于体型系数的公式。

如：

人的临床剂量为Xmg/kg,换算成大鼠的剂量：

大鼠的剂量＝（Xmg/kg×

70kg×

0.018）/200g

＝（Xmg/kg×

0.018）/0.2kg

＝6.3Xmg/kg。

这也就是说，按单位体重的剂量来算，大鼠的等效剂量相当于人的6.3倍。

在这里，我们要看到每种动物的体重（包括人），在上表中以蓝色显示的。

还要注意到折算系数，也就是表中以红色所示的。

将人的剂量转换成哪种动物的，就在相应的动物那一列下找到与人的相交的地方的折算系数，将剂量乘以折算系数，再乘上人的体重与那种动物体重的比值。

注意体重的单位要化成一致。

这个折算系数是以上表中蓝色所示的标准体重计算得来的。

依此类推，我们可以算出小鼠、豚鼠等其它动物剂量与人的比值。

小鼠的剂量＝（Xmg/kg×

0.0026）/20g

0.0026）/0.02kg＝9.1Xmg/kg。

豚鼠的剂量＝（Xmg/kg×

0.031）/400g

0.031）/0.4kg＝5.42Xmg/kg。

兔的剂量＝（Xmg/kg×

0.07）/1.5kg＝3.27Xmg/kg。

猫的剂量＝（Xmg/kg×

0.078）/2.0kg＝2.73Xmg/kg。

猴的剂量＝（Xmg/kg×

0.06）/4.0kg＝1.05Xmg/kg。

狗的剂量＝（Xmg/kg×

0.32）/12kg＝1.87Xmg/kg。

注意，人的临床剂量常会以×

×

mg／d或×

g／d来表示，这时我们一定要把它转化成×

mg/kg或×

g／d才能以上式来折算。

其实徐叔云教授主编的《药理实验方法学》在第三版中也列也出了×

mg／只的计算公式。

某药，成人每天服用50mg计算大鼠的等效剂量。

大鼠的等效剂量＝50mg/60kg×

6.3=5.25mg/kg

在这里，我们一般把成人的体重按60kg来算比较合理。

尽管在这个表中，成人的标准体重设为70kg。

我们平时在试验中可利用此公式推算大鼠的等效剂量，大鼠的等效剂量=6.3x成人的给药剂量，那么如果我们给药方案改变该公式是否依然可以使用。

既然是“等效剂量”，就要有可比性。

人的给药方案如何，大鼠的方案也应如此。

只是，有的情况下要作一个变通。

比如，口服，我们一般就变成灌胃。

人是一天三次，动物一般也可以一天两次或三次。

当然，这里有一点值得提出，就是我们一般每天给两次药的情况已是不多。

多数情况下一天给一次药。

可把两次剂量加在一起。

这样做，与一天两次有所差异。

但对于整个实验来说，如果各组间给药方式一样，那也就可以剂同对比了。

如果是做药动学实验，因不同给药方式相差较大，则另当别论了。

根据上述表格和原理，我们就可以来编制下面这样一个简表。

这样，我们不必去翻阅厚重的药理实验参考书，就一目了然。

这个表虽然是以体重的比来计算剂量，但实际上计算的是体表面积。

这种换算关系的前提是：

各种动物对某药的敏感程度是一样的。

见下表：

不同实验动物与人的等效剂量比值（注：

剂量按mg/kg算）

动物

剂量比值

9.1

6.3

5.42

3.27

2.73

1.05

1.87

其实这个表人的体重依然是按70Kg来算的，如果人的体重按60kg计算，那这个简表就要修正了。

按人体重60kg计算：

实验动物用剂量＝人的剂量×

60×

1.11×

折算系数／动物体重。

而原有的计算方法为：

70×

这样，相当于简表中的数字都要乘以60×

1.11/70=0.95

结果如下：

8.65

5.98

5.15

3.11

2.59

0.998

1.78

其实这个表，还是有问题的：

比如猴子和人的等效剂量比值为0.06，据此算出猴的剂量＝Xmg/kg×

0.06/4.0kg＝1.05Xmg/kg即猴和人的剂量换算比例为1.05；

或者人的体重按照60kg来算，猴和人的剂量换算比例为0.998。

这个都有问题。

如果你再按照陈奇主编的《中药药理研究方法学》上，猴子和人的等效剂量比值为0.16，据此算出猴的剂量＝Xmg/kg×

0.16/4.0kg＝2.8Xmg/kg

1.05和2.8这个差异就比较大了。

那么这两个数据到底那个才是正确的呢？

那么我们再用体型系数的方法计算一下，来看看到底那个是正确的。

猴的剂量＝（体型系数猴×

W猴2/3）/（体型系数人×

W人2/3）×

X/4

＝（0.111×

42/3）/（0.1×

702/3）×

X/4mg/kg

≈2.88Xmg/kg

所以，从这个计算结果来看猴子和人的等效剂量比值为0.16，而不是0.06。

猴和人的剂量换算比例可能为2.8左右。

其实徐叔云教授主编的《药理实验方法学》在第三版中也做了修改，把猴子和人的等效剂量比值改为0.16。

为了看看别的实验动物折算系数是否正确，那么我们来验证下各常用实验动物折算系数。

验证如下：

小鼠体型系数：

0.06 

标准体重：

20g=0.02kg

小鼠的折算系数＝（体型系数小鼠×

W小鼠2/3）/（体型系数人×

W人2/3）

＝（0.06×

0.022/3）/0.1×

X/0.4

＝0.004364/1.723

＝0.00253

大鼠体型系数：

0.09 

200g=0.2kg

大鼠的折算系数＝（体型系数大鼠×

W大鼠2/3）/（体型系数人×

W人2/3）＝（0.09×

0.22/3）/0.1×

＝0.030618/1.723

＝0.01777

＝0.018

豚鼠体型系数：

0.099 

400g=0.4kg

豚鼠的折算系数＝（体型系数豚鼠×

W豚鼠2/3）/（体型系数人×

W人2/3）＝（0.099×

0.42/3）/0.1×

＝0.05358/1.723

＝0.031

兔体型系数：

0.093 

1.5kg

兔的折算系数＝（体型系数兔×

W兔2/3）/（体型系数人×

＝（0.093×

1.52/3）/0.1×

702/3）

＝0.1220/1.723

＝0.07

猫体型系数：

0.082 

2.0kg

猫的折算系数＝（体型系数猫×

W猫2/3）/（体型系数人×

＝（0.082×

2.02/3）/0.1×

＝0.1305/1.723

＝0.076

狗体型系数：

0.104 

12kg

狗的折算系数＝（体型系数狗×

W狗2/3）/（体型系数人×

＝（0.104×

122/3）/0.1×

＝0.5496/1.723

＝0.32

猴体型系数：

0.111 

标准体重：

4.0kg

猴的折算系数＝（体型系数猴×

42/3）/0.1×

＝0.2810/1.723

＝0.163

其实，第二个剂量折算表就是根据体表面积、体型系数的公式将不同种属动物的标准体重而得到的体表面积相比而得到的！

我们知道了这种算法之后，我们就可以把第一个表格改正为下面的这张表了。

其实徐叔云教授主编的《药理实验方法学》第三版修改后的数据和这张表格的数据基本上是相同的。

人和动物间按体表面积折算的等效剂量比值（更正）

（20g）（200g）（400g）（1.5kg）（2.0kg）（4.0kg）（12kg）（70kg）

0.0025

0.076 

0.163

而根据更正后的人和动物间按体表面积折算的等效剂量比值表，我们可以将不同实验动物与人的等效剂量比值结果更正如下：

实验动物与人剂量折算简表如下所示：

剂量按mg/kg算，人体按70kg算）（更正）

2.66

2.85

在此再说明一下，关于小鼠的体型系数，目前仍有争论。

0.06算出的体表面积比实测的体表面积要小一些。

目前有人实测后认为小鼠的体型与大鼠相似，体型系数接近0.089。

如果照此算来，小鼠与人相比剂量倍数还要增加。

从以上我们的计算可以看出，我们的计算都是以体表面积来计算的。

为什么说要按体表面积来算才是准确的呢？

起初人们也以为是直接按体重比计算剂量就可以了，后来发现是不正确的。

经研究才知，是与体表面积基本成正比的。

这是根据能量代谢的原理而得出的，认为人和动物向外界环境中放热的量与其体表面积成正比。

很多研究指出：

基础代谢率、热卡、肝肾功能、血药浓度、血药浓度_时间曲线的曲线下面积（AUC）、肌酐（Cr）、Cr清除率、血液循环等都与体表面积基本成正比，因此按照动物体表面积计算药物剂量比体重更为合理。

应该说，这是一种理想化的推论。

在目前没有更好的、也没有更方便的换算方法的前提下，我们可以把当前这种折算关系当作一种重要的参考。

值得一提的是，这个换算方法只是一个重要参考而已。

遇到有很大种属差异的药物或化合物，上述换算关系就相差很大了。

这一点要引起大家的关注。

二、体型系数计算法

体型系数是人们根据不同动物的体重与体表面积之间的关系计算出来的。

不同的动物有不同的体型系数。

不少动物（包括人）的体型系数在0.09～0.1。

体表面积＝体型系数×

体重2/3，注意，体表面积是与体重的2/3次方成正比的。

而我们按折算系数计算的时候，是直接按体重给药的。

也就是说，剂量是与体重成正比的，而不是与体重的2/3次方。

这就是上面说的偏差的来源。

常用实验动物的体型系数如下表。

不同动物的体型系数

体型系数

0.099

0.093

0.082

0.104

0.111

0.1

下面我们来算一下，各种动物之间的体表面积比。

一个70kg的人与一只200g的大鼠的体表面积。

人的体表面积＝0.1×

702/3=1.722

大鼠的体表面积＝0.09×

0.22/3=0.0306

体表面积比（大鼠／人）＝0.0306/1.722=0.0177≈0.018

再算体重为20g的小鼠的。

小鼠的体表面积＝0.06×

0.022/3=0.00436

体表面积比（小鼠／人）＝0.00436/1.722=0.00254≈0.0025

可以看出，这个计算结果与前面我们所说的那个表基本是一致。

事实上，那个表就是根据体型系数算出来的。

这个按体型系数计算体表面积的公式被称为Mech公式。

于1879年发表。

这个公式的发表，可以说，对于科学界起到了一个很好的推动作用。

也使得我们从事药理、实验动物学的科研人员有了很好的借鉴。

从上述解析也可以看出，我们完全可以信任第一个表中所列出的折算系数，当然，也完全可以信任后面我编制的那个简表。

因为，这一切都是由体型公式计算得来的，也就是说，是按体表面积来计算等效剂量的。

为什么这么说呢？

那么我们下面就来算一算。

来做个对比。

以大鼠为例。

设人的剂量为Xmg/kg， 

体重70kg

体重为150g时：

按折算系数算：

大鼠的剂量＝6.3Xmg/kg

150g大鼠的总给药量为：

0.15×

6.3Xmg/kg＝0.945Xmg/kg

按体表面积计算：

0.152/3=0.02525

人的体表面积＝1.722

体表面积比（大鼠／人）＝0.02525／1.722=0.01466

Xmg/kg×

0.01466=1.0262Xmg/kg

体重为180g时：

180g大鼠的总给药量为：

0.18×

6.3Xmg/kg＝1.134Xmg/kg

0.182/3=0.02853

体表面积比（大鼠／人）＝0.02853／1.722=0.0166

0.0166=1.162Xmg/kg

体重为250g时：

250g大鼠的总给药量为：

0.25×

6.3Xmg/kg＝1.575Xmg/kg

0.252/3=0.03555

体表面积比（大鼠／人）＝0.03555／1.722=0.02064

0.02064=1.4445Xmg/kg

体重为350g时：

大鼠的剂量＝6.3Xmg/kg

350g大鼠的总给药量为：

0.35×

6.3Xmg/kg＝2.205Xmg/kg

0.352/3=0.04454

体表面积比（大鼠／人）＝0.04454／1.722=0.02586

0.02586=1.8102Xmg/kg

从上述计算结果我们可以看出规律！

那就是，当大鼠体重小于200g时，按折算系数算出来的结果比按体表面积的结果要偏小；

而大鼠体重大于200g时，按折算系数算出来的结果比按体表面积的结果要偏大。

推广一下，当实验动物体重小于标准体重时，按折算系数算出来的结果比按体表面积的结果要偏小；

而当实验动物体重大于标准体重时，按折算系数算出来的结果比按体表面积的结果要偏大。

如果说从准确性来看，当然是按实际的体表面积来算为好。

可是要是从方便性来看，当然是按折算系数来计算为好。

对于两种计算等效剂量方法的误差问题我们应该怎么看待呢。

三、误差的分析

从上面我们已经知道按折算系数计算会产生误差。

这种误差应该说是属于系统误差。

是由于这个公式本身给我们的实验带来的误差。

还有一种误差是我们在实验中实际给药时，由于称体重、给药时的不准而产生的，那就不是我们要探讨的问题了。

我们仍以大鼠为例来讨论这个误差问题。

设人的剂量为Umg/kg,体重为70kg。

设大鼠的体重为Xkg

按折算系数计算得出的Xkg大鼠的用药量为Y1。

则：

Y1=U×

6.3×

X=6.3UX

按实际体面表面计算得出的Ｘkg大鼠的用药量为Y2。

Y2=0.09×

Ｘ2/3/1.722×

U×

70=3.66UX2/3

这样，我们就构筑了两个函数关系式。

函数Y1是一个正比例函数，其值是与X成直线相关的。

函数Y2是一个指数函数，其值是随X增大的，但不成直线。

这两个函数在什么时候相等呢？

很显然，就是当X＝0.2的时候。

因为折算系数是当大鼠体重为0.2kg时来计算的。

根据前面计算的结果，我们可以预测到：

当X<

0.2时，函数Y2在Y1的上方，

当X>

0.2时，函数Y2在Y1的下方。

如下图所示：

我们知道，一般用于实验的大鼠，其体重大多在150～350g之间。

在药效学实验中常常选用的是180～220g的大鼠。

下面我们来计算误差。

这个误差应为相对误差。

令:

按折算系数计算的剂量＝A

按实际体表面积计算的剂量＝B

相对误差＝（A－B）／B×

100%=A/B-1

很显然，这个相对误差是有正负的。

0.2时，误差为负；

0.2时，误差为正。

因A=Y1=6.3X

B=Y2=3.66X2/3

这样，我们就可以以X为自变量，以相对误差为因变量，再构筑一个函数Y3。

Y３＝6.3X／3.66X2/3-1=1.72X1/3-1

现在我们得到了这样一个简单的函数关系式。

有什么用呢？

我们可以这个来估算按折算系数计算的剂量与实际相差多少。

如果相差不大，我们认为是可以接受的。

从图上我们可以直观地看出，当大鼠体重在200～300g时，误差不到20%。

在200g以下，是负的误差。

数据如下：

体重（kg）相对误差

0.1 

-0.201646721

0.11 

-0.175875785

0.12 

-0.151623046

0.13 

-0.128682913

0.14 

-0.106891014

0.15 

-0.086113631

0.16 

-0.06624034

0.17 

-0.04717878

0.18 

-0.028850818

0.19 

-0.011189702

0.2 

0.005862102

0.21 

0.022354576

0.038331447

0.23 

0.053831216

0.24 

0.068887982

0.25 

0.083532103

0.26 

0.097790739

0.27 

0.1116883

0.28 

0.125246811

0.29 

0.138486223

0.3 

0.151424674

0.31 

0.164078706

0.32 

0.176463451

0.33 

0.188592796

0.34 

0.200479512

0.35 

0.212135382

0.36 

0.223571297

0.37 

0.234797349

0.38 

0.245822908

0.39 

0.256656695

0.4 

0.267306836

0.41 

0.277780921

0.288086051

0.43 

0.298228878

0.44 

0.308215647

0.45 

0.318052224

0.46 

0.327744132

0.47 

0.337296577

0.48 

0.346714469

0.49 

0.356002448

0.5