七年级上册变量之间的关系练习题Word格式文档下载.docx

七年级上册变量之间的关系练习题Word格式文档下载.docx

《七年级上册变量之间的关系练习题Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《七年级上册变量之间的关系练习题Word格式文档下载.docx（14页珍藏版）》请在冰豆网上搜索。

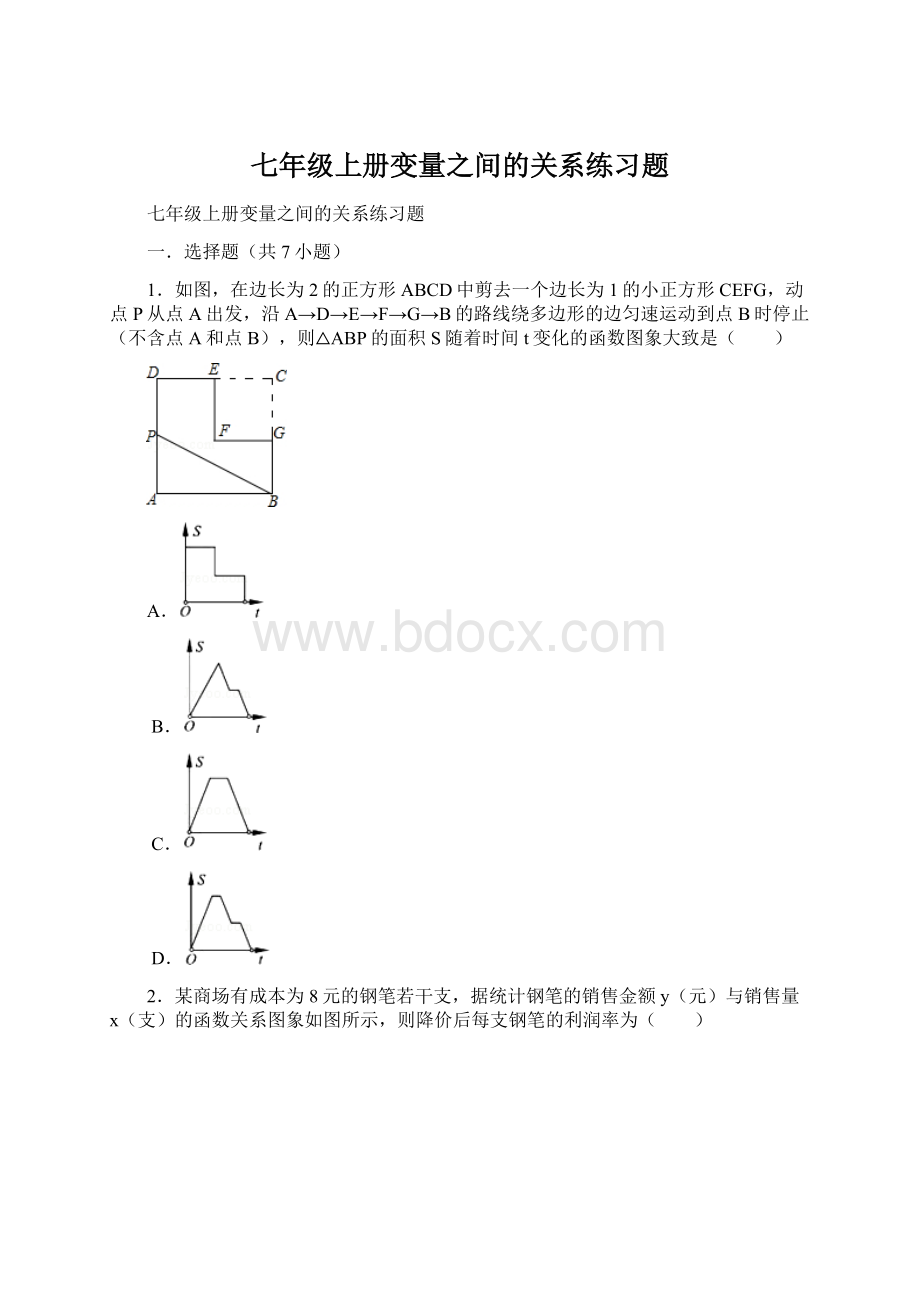
（3）图甲中的图形面积是　　．

（4）图乙中B所表示的数是　　．

11．为了加强公民的节水意识，某市制定了如下用水收费标准，每户每月的用水不超过10t时，水价为每吨2.2元；

超过10t时，超过部分按每吨2.8元收费，该市每户居民5月份用水xt（x＞10），应交水费y元，则y关于x的关系式　　．

三．解答题（共5小题）

12．“十一”期间，小明和父母一起开车到距家200千米的景点旅游，出发前，汽车油箱内储油45升，当行驶150千米时，发现油箱油箱余油量为30升（假设行驶过程中汽车的耗油量是均匀的）．

（1）求该车平均每千米的耗油量，并写出行驶路程x（千米）与剩余油盘Q（升）的关系式；

（2）当x=280（千米）时，求剩余油量Q的值；

（3）当油箱中剩余油盘低于3升时，汽车将自动报警，如果往返途中不加油，他们能否在汽车报警前回到家？

请说明理由．

13．“龟兔赛跑”的故事同学们都非常熟悉，图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系，请你根据图中给出的信息，解决下列问题．

（1）填空：

折线OABC表示赛跑过程中　　的路程与时间的关系，线段OD表示赛跑过程中　　的路程与时间的关系．赛跑的全程是　　米．

（2）兔子在起初每分钟跑多少米？

乌龟每分钟爬多少米？

（3）乌龟用了多少分钟追上了正在睡觉的兔子？

（4）兔子醒来，以48千米/时的速度跑向终点，结果还是比乌龟晚到了0.5分钟，请你算算兔子中间停下睡觉用了多少分钟？

14．如图①，在长方形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A、B、C、D路线运动，到D停止，点P的速度为每秒1cm，a秒时点P的速度变为每秒bcm，图②是点P出发x秒后，△APD的面积S1（cm2）与y（秒）的函数关系图象：

（1）根据图②中提供的信息，a=　　，b=　　，c=　　．

（2）点P出发后几秒，△APD的面积S1是长方形ABCD面积的四分之一？

15．如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

（1）探究猜想：

①∠A=30°

，∠D=40°

，则∠AED等于多少度？

②若∠A=20°

，∠D=60°

③猜想图1中∠AED、∠EAB、∠EDC的关系并说明理由．

（2）拓展应用，如图2，线段FE与长方形ABCD的边AB交于点E，与边CD交于点F．图2中①②分别是被线段FE隔开的2个区域（不含边界），P是位于以上两个区域内的一点，猜想∠PEB，∠PFC，∠EPF的关系（不要求说明理由）

16．如图1是一张长方形的纸带，将这张纸带沿EF折叠成图2，再沿BF折叠成图3．

（1）若∠DEF=20°

，请你求出图3中∠CFE度数；

（2）若∠DEF=a，请你直接用含a的式子表示图3中∠CFE的度数．

2018年04月12日185****9415的初中数学组卷

参考答案与试题解析

1．

【解答】解：

当点P在AD上时，△ABP的底AB不变，高增大，所以△ABP的面积S随着时间t的增大而增大；

当点P在DE上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；

当点P在EF上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；

当点P在FG上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；

当点P在GB上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小而减小；

故选：

D．

2．

降价后每支钢笔的价格为（1000﹣600）÷

（80﹣40）=10（元），

降价后每支钢笔的利润率为（10﹣8）÷

8×

100%=25%．

3．

根据题意可知地铁进入桥的时间x与地铁在桥上的长度y之间的关系具体可描述为：

当地铁开始进入桥时y逐渐变大，地铁完全在桥上一段时间内y不变，当地铁开始出来时y逐渐变小，故反映到图象上应选B．

B．

4．

根据函数图象可以知：

从0到2，y随x的增大而增大，经过了2秒，P运动了2cm，因而CG=2cm，BC=4cm，故①正确；

经过了3秒，P运动了3cm，因而DE=3cm，故②正确；

P在CD段时，底边AB不变，高不变，因而面积不变，由图象可知CD=2cm，面积y=

×

3×

4=6cm2，故③正确；

图2中的N点表示第12秒时，表示点P到达H点，△ABP的面积是

cm2．

四个结论都正确．

5．

由题意，得

y=20﹣5x．

∵0≤y≤20，

∴0≤20﹣5x≤20，

∴0≤x≤4，

∴y=20﹣5x的图象是一条线段．

∵k=﹣5＜0，

∴y随x的增大而减小，

∴y=20﹣5x是降函数，且图象为1条线段．

C．

6．

∵x=3时，及R从N到达点P时，面积开始不变，

∴PN=3，

同理可得QP=5，

∴矩形的周长为2（3+5）=16．

7．

A、应为：

作线段AB，使AB=α，故本选项错误；

B、应为：

延长线段AB到C，BC=AB，故本选项错误；

C、作∠AOB，使∠AOB=∠α，故本选项正确；

D、需要说明半径的长，故选项错误．

8．

由2x+y=4，得

y=﹣2x+4．

故答案是：

9．

依题意有：

y=1000×

1.5%x×

（1﹣20%）+1000=12x+1000，

当x=3时，y=12×

3+1000=1036．

故答案为：

y=12x+1000，1036．

10．

（1）动点P在BC上运动时，对应的时间为0到4秒，易得：

BC=2cm/秒×

4秒=8cm．

故图甲中BC的长度是8cm；

（2）由

（1）可得，BC=8cm，则：

图乙中A所表示的数是：

BC×

AB=

6=24（cm2）．

故图乙中A所表示的数是24；

（3）由图可得：

CD=2×

2=4cm，DE=2×

3=6cm，

则AF=BC+DE=14cm，

又由AB=6cm，

则甲中的梯形面积为AB×

AF﹣CD×

DE=6×

14﹣4×

6=60（cm2）．

故图甲中的图形面积为60cm2；

（4）根据题意，动点P共运动了BC+CD+DE+EF+FA=（BC+DE）+（CD+EF）+FA=14+6+14=34（cm），

其速度是2cm/秒，34÷

2=17（秒）．

故图乙中B所表示的数是17．

故答案为8cm；

24；

60cm2；

17．

11．

∵该市每户居民5月份用水xt（x＞10），

∴应交水费y元关于x的关系式为：

y=10×

2.2+2.8（x﹣10）=2.8x﹣6．

y=2.8x﹣6．

12．

（1）该车平均每千米的耗油量为（45﹣30）÷

150=0.1（升/千米），

行驶路程x（千米）与剩余油盘Q（升）的关系式为Q=45﹣0.1x；

（2）当x=280时，Q=45﹣0.1×

280=17（L）．

答：

当x=280（千米）时，剩余油量Q的值为17L．

（3）（45﹣3）÷

0.1=420（千米），

∵420＞400，

∴他们能在汽车报警前回到家．

13．

（1）∵乌龟是一直跑的而兔子中间有休息的时刻；

∴折线OABC表示赛跑过程中兔子的路程与时间的关系；

线段OD表示赛跑过程中乌龟的路程与时间的关系；

由图象可知：

赛跑的路程为1500米；

兔子、乌龟、1500；

（2）结合图象得出：

兔子在起初每分钟跑700米．

1500÷

30=50（米）

乌龟每分钟爬50米．

（3）700÷

50=14（分钟）

乌龟用了14分钟追上了正在睡觉的兔子．

（4）∵48千米=48000米

∴48000÷

60=800（米/分）

（1500﹣700）÷

800=1（分钟）

30+0.5﹣1×

2=28.5（分钟）

兔子中间停下睡觉用了28.5分钟．

14．

（1）依函数图象可知：

当0≤x≤a时，S1=

8a=24即：

a=6

当a＜x≤8时，S1=

[6×

1+b（8﹣6）]=40即：

b=2

当8＜x≤c时，①当点P从B点运动到C点三角形APD的面积S1=

10=40（cm2）一定，所需时间是：

8÷

2=4（秒）

②当点P从C点运动到D点：

所需时间是：

10÷

2=5（秒）

所以c=8+4+5=17（秒）

故答案为：

a=6，b=2，c=17．

（2）∵长方形ABCD面积是：

10×

8=80（cm2）

∴当0≤x≤a时，

8x=80×

即：

x=5；

当12≤x≤17时，

2（17﹣x）=80×

x=14.5．

∴点P出发后5秒或14.5秒，△APD的面积S1是长方形ABCD面积的四分之一

15．

（1）①过点E作EF∥AB，

∵AB∥CD，

∴AB∥CD∥EF，

∵∠A=30°

，

∴∠1=∠A=30°

，∠2=∠D=40°

∴∠AED=∠1+∠2=70°

；

②过点E作EF∥AB，

∵∠A=20°

∴∠1=∠A=20°

，∠2=∠D=60°

∴∠AED=∠1+∠2=80°

③猜想：

∠AED=∠EAB+∠EDC．

理由：

过点E作EF∥CD，

∵AB∥DC∴EF∥AB（平行于同一条直线的两直线平行），

∴∠1=∠EAB，∠2=∠EDC（两直线平行，内错角相等），

∴∠AED=∠1+∠2=∠EAB+∠EDC（等量代换）．

（2）如图2，当点P在①区域时，

∴∠BEF+∠CFE=180°

∴∠PEF+∠PFE=（∠PEB+∠PFC）﹣180°

．

∵∠PEF+∠PFE+∠EPF=180°

∴∠EPF=180°

﹣（∠PEF+∠PFE）=180°

﹣（∠PEB+∠PFC）+180°

=360°

﹣（∠PEB+∠PFC）；

当点P在区域②时，如图3所示，

∵∠EPF+∠FEP+∠PFE=180°

∴∠EPF=∠PEB+∠PFC．

16．

（1）∵矩形对边AD∥BC，

∴CF∥DE，

∴图1中，∠CFE=180°

﹣∠DEF=180°

﹣20°

=160°

∵矩形对边AD∥BC，

∴∠BFE=∠DEF=20°

∴图2中，∠BFC=160°

=140°

由翻折的性质得，图3中∠CFE+∠BFE=∠BFC，

∴图3中，∠CFE+20°

∴图3中，∠CFE=120°

（2）∵矩形对边AD∥BC，

﹣a，

∴∠BFE=∠DEF=a，

∴图2中，∠BFC=180°

﹣2a，

∴图3中，∠CFE+a=180°

∴图3中，∠CFE=180°

﹣3a．