成人高考高数二笔记定理及公式Word文档下载推荐.docx
《成人高考高数二笔记定理及公式Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《成人高考高数二笔记定理及公式Word文档下载推荐.docx(67页珍藏版)》请在冰豆网上搜索。
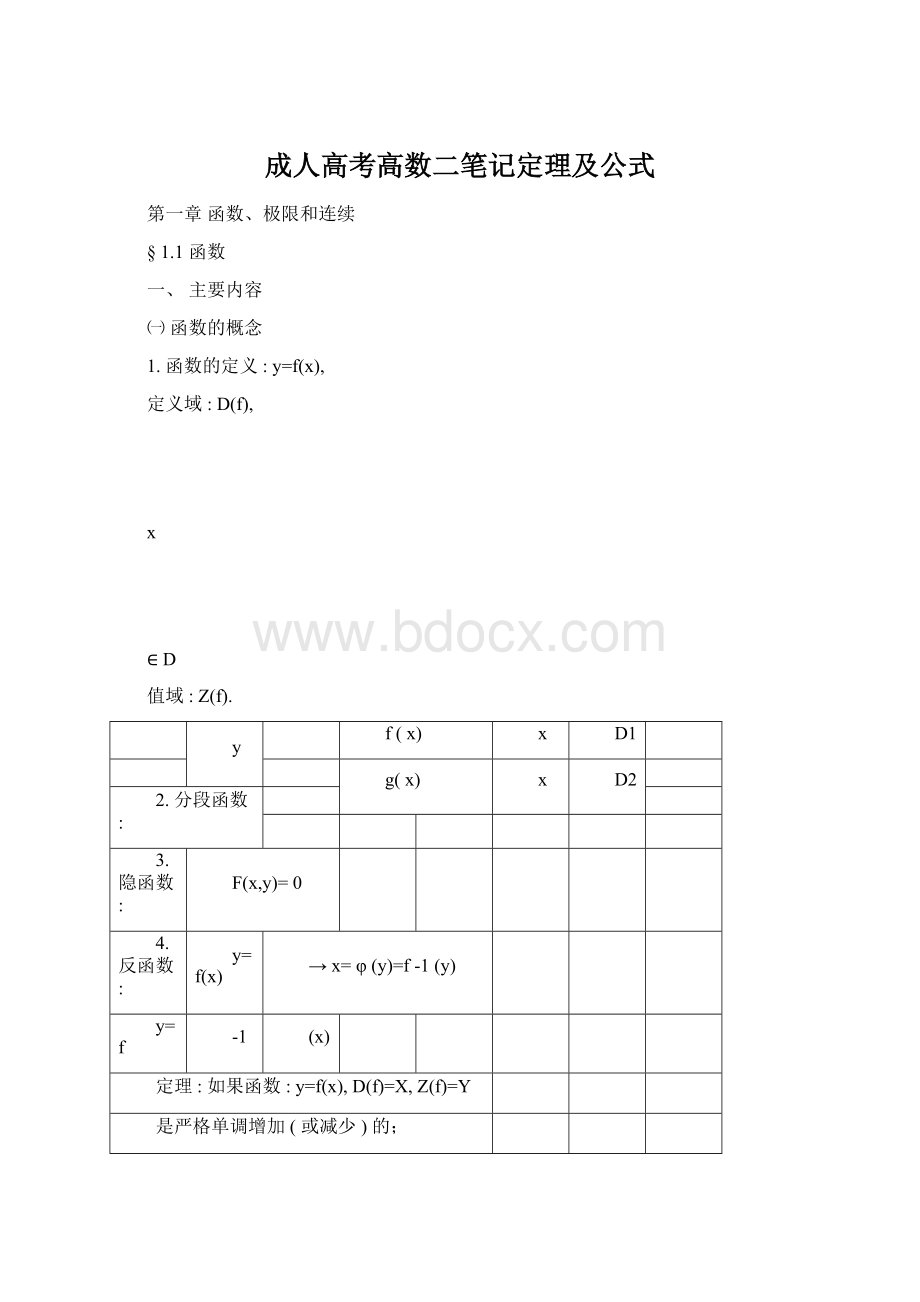
在D内单调减少(
若f(x1)<f(x
2),
则称f(x)在D内严格单调增加(
若f(x1)>f(x2),
则称f(x)在D内严格单调减少()。
2.函数的奇偶性:
D(f)关于原点对称
偶函数:
f(-x)=f(x)
奇函数:
f(-x)=-f(x)
3.函数的周期性:
周期函数:
f(x+T)=f(x),x∈(-∞,+∞)
周期:
T——最小的正数
4.函数的有界性:
|f(x)|≤M,x∈(a,b)
㈢基本初等函数
1.常数函数:
y=c,(c为常数)
2.幂函数:
y=xn,(n为实数)
3.指数函数:
y=ax,(a>0、a≠1)
4.对数函数:
y=logax,(a>0、a≠1)
5.三角函数:
y=sinx,y=conx
y=tanx,y=cotx
y=secx,y=cscx
6.反三角函数:
y=arcsinx,y=arcconx
y=arctanx,y=arccotx
㈣复合函数和初等函数
1.复合函数:
y=f(u),u=φ(x)
y=f[φ(x)],x∈X
2.初等函数:
由基本初等函数经过有限次的四则运算(加、减、乘、除)和复合所构成的,并且能用一个数学式子表示的函
数
1.2极限
㈠极限的概念
1.数列的极限:
limynA
n
称数列yn以常数A为极限;
或称数列yn收敛于A.
若yn的极限存在yn必定有界.
2.函数的极限:
⑴当x时,f(x)的极限:
lim
A
limf(x)A
⑵当xx0时,f(x)的极限:
xx0
左极限:
xx0
右极限:
⑶函数极限存的充要条件:
limf(x)A
limf(x)
定理:
㈡无穷大量和无穷小量
1.无穷大量:
limf(x)
称在该变化过程中f(x)为无穷大量。
X再某个变化过程是指:
x
xx0,xx0,xx0
2.
无穷小量:
lim
f(x)
称在该变化过程中
f(x)为无穷小量。
3.
无穷大量与无穷小量的关系:
(f(x)0)
f(x)
4.无穷小量的比较:
lim0,lim0
lim0
⑴若,则称β是比α较高阶的无穷小量;
limc
⑵若(c为常数),则称β与α同阶的无穷小量;
lim1
⑶若,则称β与α是等价的无穷小量,记作:
β~α;
⑷若,则称β是比α较低阶的无穷小量。
若:
则:
1~1,2~2;
㈢两面夹定理
1.数列极限存在的判定准则:
设:
ynxnzn(n=1、2、3)
且:
limynlimzna
nn
limxna
2.函数极限存在的判定准则:
对于点x0的某个邻域内的一切点
(点x0除外)有:
g(x)f(x)h(x)
limg(x)limh(x)A
xx0xx0
㈣极限的运算规则
若:
limu(x)A,limv(x)B
①lim[u(x)v(x)]
limu(x)
limv(x)A
B
②lim[u(x)v(x)]limu(x)
limv(x)
③limu(x)
limu(x)
(limv(x)
0)
v(x)
limv(x)
推论:
①lim[u1(x)u2(x)un(x)]
limu1(x)limu2(x)limun(x)
②lim[cu(x)]
climu(x)
③lim[u(x)]n
[limu(x)]n
㈤两个重要极限
sinx
sin
(x)
1.x
或(x)0
1)x
lim(1
e
lim(1x)x
2.x
x0
1.3
㈠函数的连续性
连续
1.函数在
x0
处连续:
f(x)在
x0的邻域内有定义,
1o
limx0
lim[f(x0x0
x)f(x0)]
o
f(x0)
xx
f(x0)
左连续:
x
右连续:
2.函数在x0处连续的必要条件:
f(x)在x0处连续f(x)在x0处极限存在
3.函数在x0处连续的充要条件:
limf(x)f(x0)
limf(x)f(x0)
4.函数在
a,b上连续:
f(x)在a,b上每一点都连续。
在端点a和b连续是指:
limf(x)
xa
limf(x)
xb
a+0
5.函数的间断点:
f(a)
左端点右连续;
f(b)
右端点左连续。
b-x
若f(x)在x0处不连续,则x0为f(x)的间断点。
间断点有三种情况:
1o)x(f在x0处无定义;
不存在;
)x(f在x0处有定义,且
3
存在,
但xx
。
两类间断点的判断:
1o第一类间断点:
limf(x)limf(x)
特点:
xx
和xx
都存在。
可去间断点:
存在,但
,或)x(f
在x0处无定义。
2o第二类间断点:
limf(x)lim
和xx0
至少有一个为∞,
或xx0
振荡不存在。
无穷间断点:
xx
至少有一个为∞
㈡函数在x0处连续的性质
1.连续函数的四则运算:
f(x0)limg(x)g(x0)
设xx
,xx
lim[f(x)
g(x)]
g(x0)
limg(x)0
2.复合函数的连续性:
yf(u),
lim(x)
u
(x0
(x),
),
(x0)
f[(x)]
f(u)
f[
(x0)]
limf[(x)]
f[lim(x)]
f[(x0)]
3.反函数的连续性:
yf(x),xf1(x),y0f(x0)
limf(x)f(x0)
limf1(y)f1(y0)
yy0
㈢函数在[a,b]上连续的性质
1.最大值与最小值定理:
f(x)在[a,b]
上连续
f(x)在[a,b]
上一定存在最大值与最小值。
+M
M
f(x)
0abx
m
-M
a
b
2.有界定理:
f(x)在[a,b]
上一定有界。
3.介值定理:
在[a,b]
在(a,b)
内至少存在一点
,使得:
f(
c
,
其中:
C
0aξb
0aξ1ξ2bx
f(x)在[a,b]上连续,且f(a)与f(b)异号
在(a,b)内至少存在一点,使得:
f()0。
4.初等函数的连续性:
初等函数在其定域区间内都是连续的。
第二章一元函数微分学
2.1导数与微分
一、主要内容
㈠导数的概念
1.导数:
f(x)在x0的某个邻域内有定义,
f(x0
x)f(x0)
lim
0x
f(x)f(x0)
yxx0
dy
dx
f
(x0)lim
2.左导数:
右导数:
f(x)在x0的左(或右)邻域上连续在
其内可导,且极限存在;
(或:
limf(x))
3.函数可导的必要条件:
f(x)在x0处可导f(x)在x0处连续
4.函数可导的充要条件:
y
xx0
f(x0)存在
f(x0),
且存在。
5.导函数:
(a,b)
f(x)在(a,b)内处处可导。
6.导数的几何性质:
是曲线
yf(x)上点
x0,y0
处切线的斜率。
㈡求导法则
1.基本求导公式:
2.导数的四则运算:
v)
v
1(u
uv
2(u
(v
3o
3.复合函数的导数:
(x)]
du
dx,或{f[
(x)]}
(x)](x)
☆注意{f[(x)]}与
(x)]的区别:
{f[
表示复合函数对自变量
x求导;
(x)]表示复合函数对中间变量
(x)求导。
4.高阶导数:
f(x),
或f(3)(x)
f(n)(x)
[f(n
1)(x)],
(n2,3,4)
函数的n阶导数等于其n-1导数的导数。
㈢微分的概念
1.微分:
f(x)在x的某个邻域内有定义,
yA(x)xo(x)
A(x)与x无关,o(x)是比x较高
limo(x)0
阶的无穷小量,即:
x0x
则称
x处可微,记作:
A(x)
dyA(x)dx
(x0)
2.导数与微分的等价关系:
f(x)在x处可微f(x)在x处可导,
f(x)A(x)
3.微分形式不变性:
dyf(u)du
不论u是自变量,还是中间变量,函数的
微分dy都具有相同的形式。
2.2中值定理及导数的应用
㈠中值定理
1.罗尔定理:
f(x)满足条件:
10在[a,b]上连续;
.
30.f(a)f(b).
在(a,b)内至少存在一点,
使得f()0.
yf()f()f(x)
aoξbxaoξbx
2.拉格朗日定理:
10
在[a,b]上连续,
在(a,b)内至少存
在一点,使得:
20
在(a,b)内可导;
f()
㈡罗必塔法则:
(0,
型未定式)
f(x)和g(x)满足条件:
(或)
limg(x)
2o在点a的某个邻域内可导,且g(x)
0;
A,(或)
xa(
)g(x)
A,
xa()g(x)
xa()g(x)
☆注意:
1o法则的意义:
把函数之比的极限化成了它们导数之比的极限。
2o若不满足法则的条件,不能使用法则。
即不是0型或型时,不可求导。
3o应用法则时,要分别对分子、分母
求导,而不是对整个分式求导。
4o若f(x)和g(x)还满足法则的条件,
可以继续使用法则,即:
A(或
xa()g(x)
xa()g(x)
5o若函数是0
型可采用代数变
型;
若是1
形,化成0或
0,
型可
采用对数或指数变形,化成
0或
型。
㈢导数的应用
1.切线方程和法线方程:
yf(x),M(x0,y0)
切线方程:
法线方程:
yy0f(x0)(xx0)
(xx0),(f(x0)0)
2.曲线的单调性:
⑴f(x)0x(a,b)f(x)在(a,b)内单调增加;
f(x)0x(a,b)f(x)在(a,b)内单调减少
⑵
f(x)0x(a,b)在(a,b)内严格单调增加;
f(x)0x(a,b)在(a,b)内严格单调减少
3.函数的极值:
⑴极值的定义:
设f(x)在(a,b)内有定义,x0是(a,b)内的一点;
若对于x0的某个邻域内的任意点xx0,都有:
f(x0)f(x)[或f(x0)f(x)]
则称f(x0)是f(x)的一个极大值(或极小值),
称x0为f(x)的极大值点(或极小值点)。
⑵极值存在的必要条件:
10.f(x)存在极值f(x0)
20.f(x0)存在。
f(x0)0
x0称为f(x)的驻点
⑶极值存在的充分条件:
定理一:
10.f(x)在x0处连续;
20.f(x0)0或f(x0)不存在;
f(x0)是极值;
x0是极值点。
30.f(x)过x0时变号。
当x渐增通过x0时,f(x)由(+)变(-);
则f(x0)为极大值;
当x渐增通过x0时,f(x)由(-)变(+);
则f(x0)为极小值。
10.f(x0)0;
f(x0)是极值;
定理二:
20.f(x0)存在。
x0是极值点。
若
0,则f(x0)
(x0)
,则
为极大值;
为极小值。
驻点不一定是极值点,极值点也不一定是驻点。
4.曲线的凹向及拐点:
⑴若f(x)0,xa,b;
则f(x)在(a,b)内是上凹的(或凹的),(∪);
⑵若f(x)0,xa,b;
则
f(x)在(a,b)内是下凹的(或