球的组合体问题1球的组合体问题最全分类和解法研究Word下载.docx
《球的组合体问题1球的组合体问题最全分类和解法研究Word下载.docx》由会员分享,可在线阅读,更多相关《球的组合体问题1球的组合体问题最全分类和解法研究Word下载.docx(62页珍藏版)》请在冰豆网上搜索。
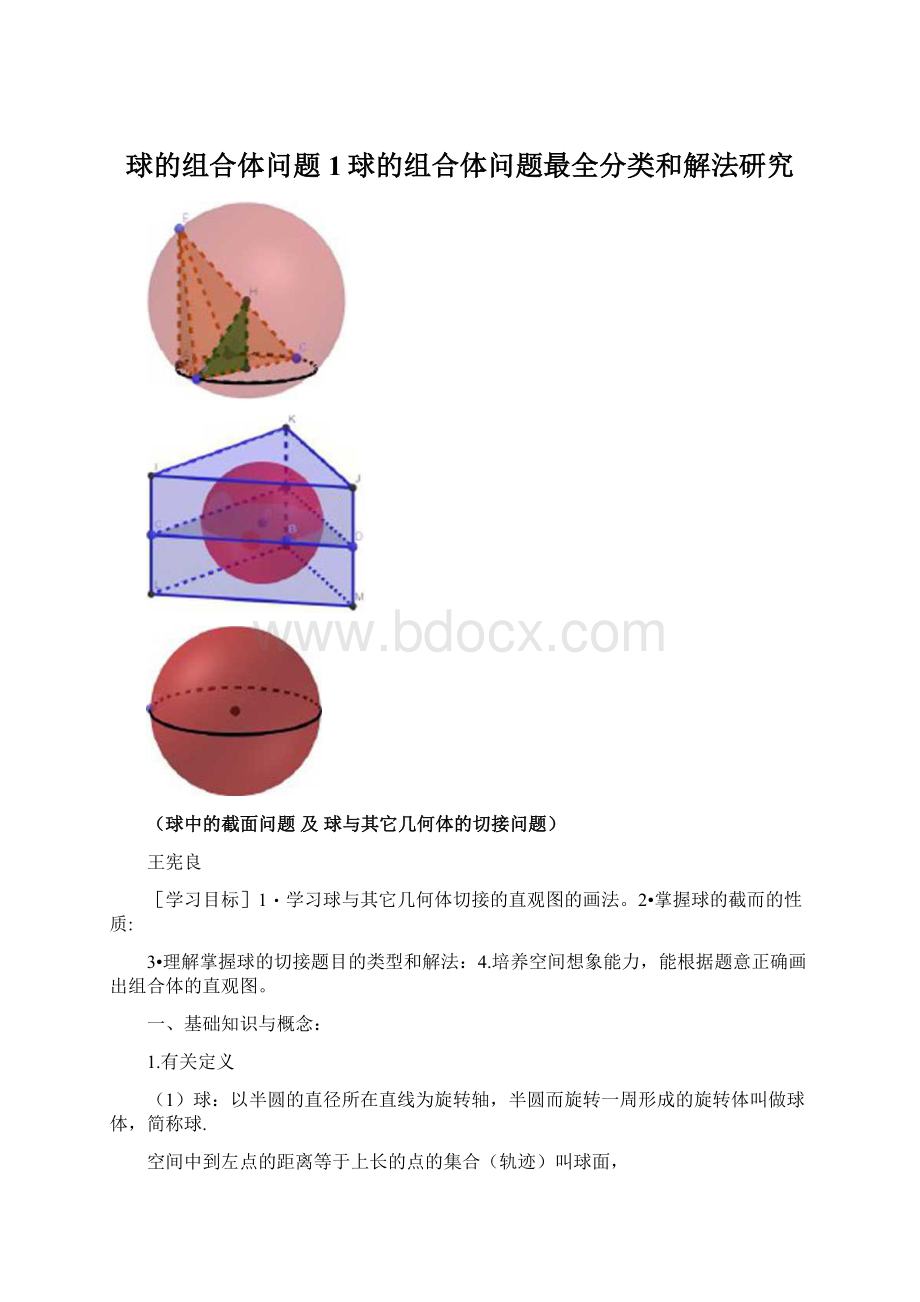
圆柱体轴截而矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;
结论6:
直棱柱与该棱柱的外接圆柱体有相同的外接球:
结论7:
圆锥体的外接球球心在圆锥的髙所在的直线上:
结论8:
圆锥体轴截而等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;
结论9:
侧棱相等的棱锥与该棱锥的外接圆锥有相同的外接球.
(3)终极利器:
勾股定理.正弦定理及余弦上理(解三角形求线段长度):
3.内切球的有关知识与方法
(1)若球与平面相切,则切点与球心连线与切而垂直・(与直线切圆的结论有T性)・
(2)内切球球心到多而体各而的距离均相等,外接球球心到多而体各顶点的距离均相等(类比:
与多边形的内切圆"
卜接圆)
(3)正多而体的内切球和外接球的球心重合.
(4)正棱锥的内切球和外接球球心都在高线上,但不一泄重合.
4.基本方法:
(1)构造三角形利用相似比和勾股泄理;
(2)体积分割是求内切球半径的通用做法(等体积法)・
二、理清位置,学会画图
先画一个大圆与一个或两个小圆。
1•多面体的外接球(球包体)
模型仁球包直柱(直锥):
有垂直于底而的侧棱(有垂底侧边棱)
球包四棱柱
速算:
球径公式
球包三棱柱速算:
注:
凡是有一条侧棱垂直于底面的柱或锥,都能补成同球内接圆柱,则都可用以下公式求其夕偎球的
①对于正三角形、等腰直角三角形、一般直角三角形:
√2r=——a7
■
2
球径公式:
R=Jt]+r2,
(厂为底面外接圆半径)
关键:
构建Rt△
②对于一般三角形:
SinASinBSinC
√6a
4a2+3h2^^6Λ^^
/+2/『
4Λ
模型2:
“顶点连心”锥:
锥体的顶点与球心及其在底而的投影(都是底面多边形外接圆的圆心)两心一顶连成线,构建Rt∆
实例:
正棱锥
球径计算方程:
(II-R)2+r2=R2Ir一IhR+r2=0=>
/?
=
72/7
(h为棱锥的高,Γ为底面外接圆半径)
特别地,
(1)边长为"
正四而体的外接球半径:
R=
(2)底而边长为α,髙为力的正三棱锥的外接球半径:
R=—
(3)底面边长为"
,髙为力的正四棱锥的外接球半径:
R=
2.正多而体的内切球(体中球)
棱锥的内切球:
(由等体
圆锥的内切球:
(若圆
锥高为hf底面半径
积法)R=
3V惟
S惟农
"
hr
r+y∣h2+r2
边长为"
的正方体:
R=-
等边圆柱(母线"
人
边长"
的正八而体:
P√6
R=——a
不用记忆结果,应画好直观图,做妍由截面图,会用平面几何知识求半径。
3.正多而体的J棱切球”(与所有的棱都相切的球)
V
d
正四而体边长为"
,球半径(是对棱距
/7
正方体边长如球半径洽
正四面体边长为“,球半径力彳
离的-^)R=∙Ja
4
三.球的问题的六种题型和解法
球心可以确定球的位置,半径可以确左球的大小。
球心和半径是确龙球的两个重要的疑。
’l求球的表而积、体积、
半径或已知球的半径而求切接几何体的棱长”等是常见题目•它们的求解都离不开求球的半径Fr据此可把球的切接
问题分成六种类型。
(见思维导图)
(一)简单的一(D能直接用m+尸求解的;
(2)正方体与球的切、接;
(3)长方体内接于球(球包长方体):
对于
(1)如图
对于
(2)(3),
球心在体对角线的交点处,请先观看视频
②球与正方体的棱相切
如图:
①正方体的内切球
Cl
③正方体的外接球
说明:
①正方体的内切球:
DI
C
球与正方体的每个而都相切,切点为每个而的中心,显然球心为正方体的中心。
设正方体的棱长为d,球半径为R。
如图,截而图为正方形EFGH的内切圆,得/?
=-:
2与正方体齐棱相切的球:
球与正方体的各棱相切,切点为各棱的中点,如图作截而图,圆O为正方形EFGH的
外接圆,易得R=-UQ
3正方体的外接球:
正方体的八个顶点都在球而上,如图,以对角而AG为截面作截而图得,圆O为矩形AAlCIC
行
的外接圆,易得R=AyO=-a(作为记住)o
4球包长方体2R=y∕a2+b2+c2
下面分别就
(1)
(2)(3)种情况举例分析
例1.
(1)(2012-课标全国,8,中)平面Qf截球O的球面所得圆的半径为1,球心O到平面α的距离为承,则此球的体积为()
A.√6πB.4√3πC.4√6πD・6√3π
解:
(直接用R—卩"
求解)如图,设平而α截球O所得圆的圆心为O,则IoOIl=√Σ
∖O↑A∖=a∖,
・••球的半径P=∣O∕4∣=√Γh=√3.・•.球的体积U=∣πP3=4√3π.故选B.
例1.
(2)[2012髙考新课标理11】已知三棱锥S-ABC的所有顶点都在球O的球而上,MBC是边长为1的正三角
形,SC为球。
的直径,且SC=2;
则此棱锥的体积为()
(A)芈(B)f(C)些OoJ
【解析】
(用R2=/+尸求解)ΔABC的外接圆的半径r=g,点、O到而ABC的距离d=y∕R2-r2=理,SC为球O
3
的宜径=>点S到面ABC的距离为2d=—
另解(估算法):
=£
排除5C,D.选A.
36
此棱锥的体积为V=-SsABCχ2CI亠旦空
33436
例1∙(3)求棱长为4的正方体的外接球和内切球的体积。
解:
由题意可知,此正方体的体对角线长即为其外接球的直径2R,正方体的棱长即为其内切球的直径2r,因为正方体的棱长为4,故2R=4√3,2r=4,所以^=2√3,(或直接用公式得R==^∙×
4=2√3).r=2,从22
而匕卜接球=∙j∕tR3=~π(2、/3)3=32:
U内切球=亍龙IJ=匚一•例1.(4)棱长为1的正方体ABCD-AlBlCiDl的8个顶点都在球O的表而上,£
F分别是棱AA1,DD的中点,
则直线EF被球O截得的线段长为(
B-,C1÷
TD近
O∖ΛDi∖√2解:
俐用截面图)由题意可知,球为正方体的外接球,平而曲QQ截球所得的圆而的半径R=-T=亍因为
EFU面AA1D1D,且EF过截面圆圆心,所以直线EF被球O截得的线段为球的截面圆的直径2R=√Σ.选D
例1.(5)(2007年天津高考题)一个长方体的各顶点均在同一球而上,且一个顶点上的三条棱长分别为12»
则此
球的表面积为
解析:
关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。
长方体体对角线长为2∕C=√l2+22+32=^,所以,故球的表而积为S=4πR2=^
巩固训练:
1.能直接用RS求解的
(1)(2013-课标I,15)已知H是球O的直径力8上一点,AH:
Hβ=1:
2,&
8丄平而α,H
为垂足,α截球O所得截而的面积为π,则球O的表而积为.
1OR
平盹截球。
所得截而为圆而,圆心为H,设球。
的半径为RKIMH=-X2,=^
211
OH=R-AH^--R=-^所以。
甘沪由圆H的而积为"
得圆H的半径小所以(f)2÷
12=矗,得仔=|,所以球O的表而积S=4τM2=4τr∣=寥填粤1
(2)已知三棱锥S-ABC各顶点均在球O上,SB为球O的直径,若AB=AC=2>
ZBAC=-,三棱锥S-ABC的体3
积为4,则球O的表而积为()
A.120兀B.64兀C.32兀D.16兀
如图,在AABC中,由余弦定理,得BC=2√J,又由正弦泄理Ir=-^-,得底面AABC的外接圆半径・λ7t
SIn——
r=σA=2,又因为S.1.=lλB∙ACsin-=√3,且三棱锥S-ABC
∙v23
的体积为4,得V=lx√¾
=4,所以Λ=4√3t所以O^=-=2√3,
32
在RtAOOfA中,由勾股宦理得球半径R=OA=SA2+O"
=4,则球O的表而积S=4^2=64π.选B
(3)(2013-课标II,15)已知正四棱锥OABCD的体积为攀,底面边长为√5,则以O为球心,04为半径的球的表而积为.
【解析】设底而中心为E由球的截而性质知OE丄底WiABCD,则∖AE∖=^∖AC∖/、\
=罟,•・•体积V=^AB∖2∙∖OE∖=∖OE∖=^∙,由球的截面的性质知ZkOEA为Rt∆,.∖∖OA∖2=∖AE∖2+∖OE∖2=β.从而
以0为球心,OA为半径的球的表而积S=4π∙Q4∣2=24ττ.填24π
<
4)已知矩形ABCD的顶点都在半径为4的球0的球而上,且AB=JBC=2乩则棱锥O一ABCD的体积为O
【解析】本题主要考査球的截面性质、棱锥的休积公•式•设矩形的对角线的交点为E,则OE丄面ABCD,K1=-BD2=丄(AB2+5C2)=12,
44
由截面圆性质得OE=JRl一"
=2,
•••棱锥O-CD的体积沖*SUJCz)XOE
=i×
6×
2√3x2=8∙>
A・
(5)(2013-课标I,6)如图,有一个水平放巻的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容
器内注水,当球面恰好接触水面时测得水深为6cm,如果不讣容器的厚度,则球的体积为()
A500π.C866πQJ372π.小2048πQ
A.^—cm3B.-g—cm3C.——Cm3D.—~~m3
设水面与球的接触点(切点)为P,球心为O,则PO垂直于正方体的上表而,
Q
体上表面的距离为"
2。
设球的半径为R,则球与正方体上表而相交圆(截面圆)的半径是二
且球心到该截面的距离是R—2,故(/?
-2)'
+宀F∕72=(P-2)2+42^∕7=5.Λ√=∣π∕73=^y11(cm3).[答案】A
【点评】关键是由球的截而圆性质构造Rt∆.由勾股龙理建立关于R的方程,求出R
(6)(2015-四川绵阳一模,7)如图所示,用一边长为頁的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表而积为4π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底而的距离为()
A.
B.
cI
D.
蛋巢的底而是边长为1的正方形,所以过四个顶点截鸡蛋所得的截面圆的直
径为1,鸡蛋的表面积为4m所以球的半径为仁所以球心到截而的距离为d=
寸爭•而截而到底面的距离即为三角形的髙M所以球心到底而的距离为
【答案】D
2.求正方体的外接球的有关问题
(7)(2006年广东高考题)若棱长为3的正方体的顶点都在同一球面上,则该球的表面枳为.
要求球的表而积,只要知道球的半径即可•因为正方体内接于球,所以它的体对角线正好为球的直径,因此,求球的半径可转化为先求正方体的体对角线长,再计算半径.另解:
R斗笔,故表面积为S—仏务27汉
(8)一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为•
要求球的体积,还是先得求岀球的半径,而球的直径正好是正方体的体对角线,因此,由正方体表而积可求出棱长,6∙∕=24,.∙./=4<
=2,从而求出正方体的体对角线是2$,所以球的半径为R=^a=y∣3,故该球的体积为V=→(√3∕=4√3λ∙.
(9)(2013-天津,10)已知一个正方体的所有顶点在一个球面上.若球的体积为牙,则正方体的棱长为
【解析】设正方体的棱长为a,则正方体的外接球半径R=^3.因为球的体积为∣ττ,所以∣π√^=∣π,即-a,所以a=√3.【答案】√3
(10)如图,在正方体ABCD-A}BIClDl中,棱长为、丘,面BDB与≡A,Z)C1的重心分
别为E、F,求EF所在直线被正方体外接球截得的弦长为()
D.学
解法一:
如左图,连结AC1,BR,交点为球心0,易知点E是线段BQ】的三等分点(靠近D1),点F是线段Aq的三等分点(靠近A),又O是BDl的中点,且是AG的中点,所以
OE=-BDI=-×
^×
y∣3=-=OF,连结EF,AD1,在厶QAD冲,因为皀-=乞,
6621ODxOA
√2
->
所以
所Tw,所以△阿〜△叫,所以焙OF
OA
3√2
EF=-ADI=1∙2√3=-.作出平而OEF与球O的截面圆图象如右图,作333
(EFy∖
)=(T
MP2=OM2-OP2=R2-OP2×
√6
OP丄MN,则"
2=OE2-
冷;
在&
中,
£
=9
6"
263
1匕得MP=
7
MN=2MP=工一•选C.
解法二:
(先用空间向呈求球心到直线EF的距离OP)设外接球球心为O,如图所示,以点D为坐标原点,DA、DC、
D人所在直线分别为X轴、丫轴、Z轴建立空间直角坐标系D-λ>
z,
A1(√6,0,√6).,联Q)、Cl(0,√z6,√6).D(0,0,0).E
'
√6√62届
♦9
、O
f√6√6逅]
所以元=
r√6
√6)
333
\/
222
•/
6
/
下边同解法一。
3.求长方体的外接球的有关问题
(11)(2006年全国卷I〉已知各顶点都在一个球而上的正四棱柱髙为4,体积为16,则这个球的表而积为()・
A16;
TB20;
Tc.24tγD.32τr
正四棱柱是底面为正方形的长方体。
由长方体的体积16及高4可以求出长方体的底面边长为2,因此,长方体的长、宽、高分别为2,2,4,于是等同于例1(5),2Λ=√4+4+16=√24=2√6.R=H所以S=4庆=24龙,故选C.
(二)一般的一球心,构造直角三角形
球心是决立球的位宜的关键点,泄球心的方法有:
1扩展成同球内接圆柱或直棱柱后,再怎球心位置,在上下底而圆心连线段的中点处•(适用于有一条侧棱垂直底面的几何体)(见例2)
2根据球心到球而上四个不共面的点的距离相等确泄球心位置:
(常用于多面体中有两个直角三角形,且两个直角三角形有公
共斜边的情况,可利用直角三角形性质:
直角三角形斜边中线等于斜边一半。
得球心为直角三角形斜边中点)(见例3)
3过两个相邻三角形外接圆圆心,且垂直于两个三角形各自所在面的两条直线的交点为球心.(适用于二面角模型)
4讨论球心的位置,列方程求解,舍去一种位置(适用于球内接正棱锥);
也可不讨论球心的位苣,而由(h-R)2=R2-r2t求R.(见例5)
5其它:
构造Rt△求解。
下面分别举例探究:
1.有一条侧棱垂直底面的几何体模型
方法一:
采用扩展成同球内接圆柱或直棱柱后,再定球心位置的方法;
(结合后四3圆柱模型)
*≡-I
■■
>
1
•宀
I
图3∙1
图3・2
图3・3
题设:
如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:
确左球心O的位置(0在扩展成的同球内接圍柱上下底面圆心连线段的中点),0]是ΔABC的外心,则Ool丄
图5
平而ABC;
第二步:
算出小圆Q的半径AOI=r,(底面三角形外接圆半径r的求法:
①若底面是等边三角形f则r=-;
②若底面是RM,则匸斜边的一半;
③若底面是一般的三角形r则可用正弦走理丄=-^-=-^-=2r求解)・OOl=-AAλ=-h(A41=Λ⅛^11的高):
SinASinBSinC22
解出/?
・(可
第三步:
用勾股定理OA2=0才+OQ2=>
∕?
2=φ2+r2=>
=Jr2+(^)2
记住该公式,见后四(三)圍柱模型速算法)
方法二:
构造以球直径为斜边的球内接直角三角形,利用勾股定理求球半径题设:
如图5,PA丄平而ABC.求外接球半径・
解题步骤:
第一步:
将ΔABC画在小圆面上,A为小圆直径的一个端点,作小圆的直径AD9连接PD.则PQ必过球心6(因
为Ool丄面ABCf又PA丄面ABC,所以PAIIOOxI所以PA与Ool共面;
又ZPAD=90。
,所以PD是大圆的直径)
Oi为AABC的外心,所以OOl丄平面ABC,算出小圆Q的半径OQ=F(三种方法同前),OOl=-PAi2
利用勾股泄理求三棱锥的外接球半径:
①在RtAPAD中,(2/?
)2=PA2+(2r)2O2R=√PA2+(2r)2:
或
②在恥OOQ中,Z?
2=r2+∞12<
=>
==λ∕r2+OO12.
例2.
(1)请观看视频(例题1
注:
设正三棱柱ABC一Λ1BlCI的高为ht底面边长为aI如图2所示,D和Q分别为上下
例2.
(2).已知SEAB所在的平而与矩形ABCD所在的平面互相垂直,EA=EB=3.AD=2.ΛAEB=ω°
则多而体
E-ABCD的外接球的表面积为・
(折叠型)
法一;
补形为宜三棱柱,可改变直三棱柱的放置方式为立式.再扩展为圆柱,通过计算圆
柱的轴截面的对角线长来求球的直径:
AEAB外接圆半径
片=二EA=观,所以(2/?
)2=(2r1)2+AD2=(2v¾
2+22=16,3
所以/?
2=4,S∕'
=16∕τ;
也可以解RtΔOO1E
底面的中心根据几何体踽点,球心必落在高㈣的中点。
,込”皿”斗,借助直角三角形AoM
勾股走理,可求R=
._+—a
”2丿〔3
法二:
补形为直三棱柱,(可改变直三棱柱的放置方式为立式),再扩展为圆柱,如图,设MBE的外接圆圆心为0∣,则EQ丄ABf垂足为M,由题意EM丄而ABCD,又设矩形ABCD的外接圆圆心为球心为0∙贝IJO(Z丄而ABCD∙所
■■
以EMIlOO1,又因为M为AB中点,所以QM丄AB,则QM丄而ABE,又OOX丄面ABE,所以OOXIlOIM,得OOXMOI为矩形,所以OOλ=O2M=^=1,在RtSOOlA中,∕∙1=OlA=^EA=√3,,所以
23
R2=r}2+OO{2=4,所以外接球的表而积为Sk=I6兀・填16兀・
PyRnIyoq1o
法三:
同上图在RtzXOOrD中,Oor=OlM=—,λ=OID==——,所以=—+—=4♦S”=∖6τr;
■二2-■2244A
法四:
用公式R=
^∣r2+φ2速算,AEAB的外接圆半径为r1=√3,h=AD=2,所以R=√ΓTT=2,S,i=∖6π.
巩固训练:
1.(高考题选)已知圆柱的髙为仁它的两个底而的圆周在直径为2的同一个球的球而上,则该圆柱的体积为O
ALt3Ji_Tif兀
A•兀B.一C.一D.一
424
由题可知球心在圆柱体中心,球心与圆柱底而圆心的距离〃=?
=圆柱体上
22
下底而圆半径r=jF≡F=Jq*j=£
则圆柱体体积v=π心=苧,故选B.解法二:
求圆柱的轴截而的对角线长得球直径,(2r)2=(2/?
)2-∕γ=22-1=3.得”=耳2.已知直三棱柱ABC-AlBlG的六个顶点都在球O的球而上,若BC=3,AC=4,BC丄ACIAAI=12,则球O的半径为
A.B.2√10C•匕D.佰
由题意知,AB是AABC外接圆的直径,AB中点0为此外接圆的圆心,球心O是
三棱柱外接圆柱的中心(高的中点),连结OQ、A0「OA,得RtΔ06>
1AIJFhAB=5,得
151I/5V13
AOl=-BC=-,又OOl=-AA}=6,所以球O的半径R=I-+62=—・
222\1\2J2
求圆柱的轴截而的对角线长得球直径,
13
(2/?
)2=(2r)2+A412=AB2+BB12=25+144=169=13—得R=-
乙
3.(2015•河南驻马店调硏,13)在三棱柱ABC-A1BC中,已知丄平而ABC,AA,=2,
βC=2√3,ZBAC=萝,且此三棱柱的各个顶点都在一个球而上,则球的体积为
为R=y∣d2+r2=√12÷
(√3)2=2,则球的体积为匕疔∣×
π×
23=φ.
【答案】
32π
【解析】依题意可知,球心到平面ABC的距离为d詁A4'
=