高中数学题库之函数部分部分百题尖子生高考数学分类汇编Word格式.docx

高中数学题库之函数部分部分百题尖子生高考数学分类汇编Word格式.docx

《高中数学题库之函数部分部分百题尖子生高考数学分类汇编Word格式.docx》由会员分享，可在线阅读，更多相关《高中数学题库之函数部分部分百题尖子生高考数学分类汇编Word格式.docx（64页珍藏版）》请在冰豆网上搜索。

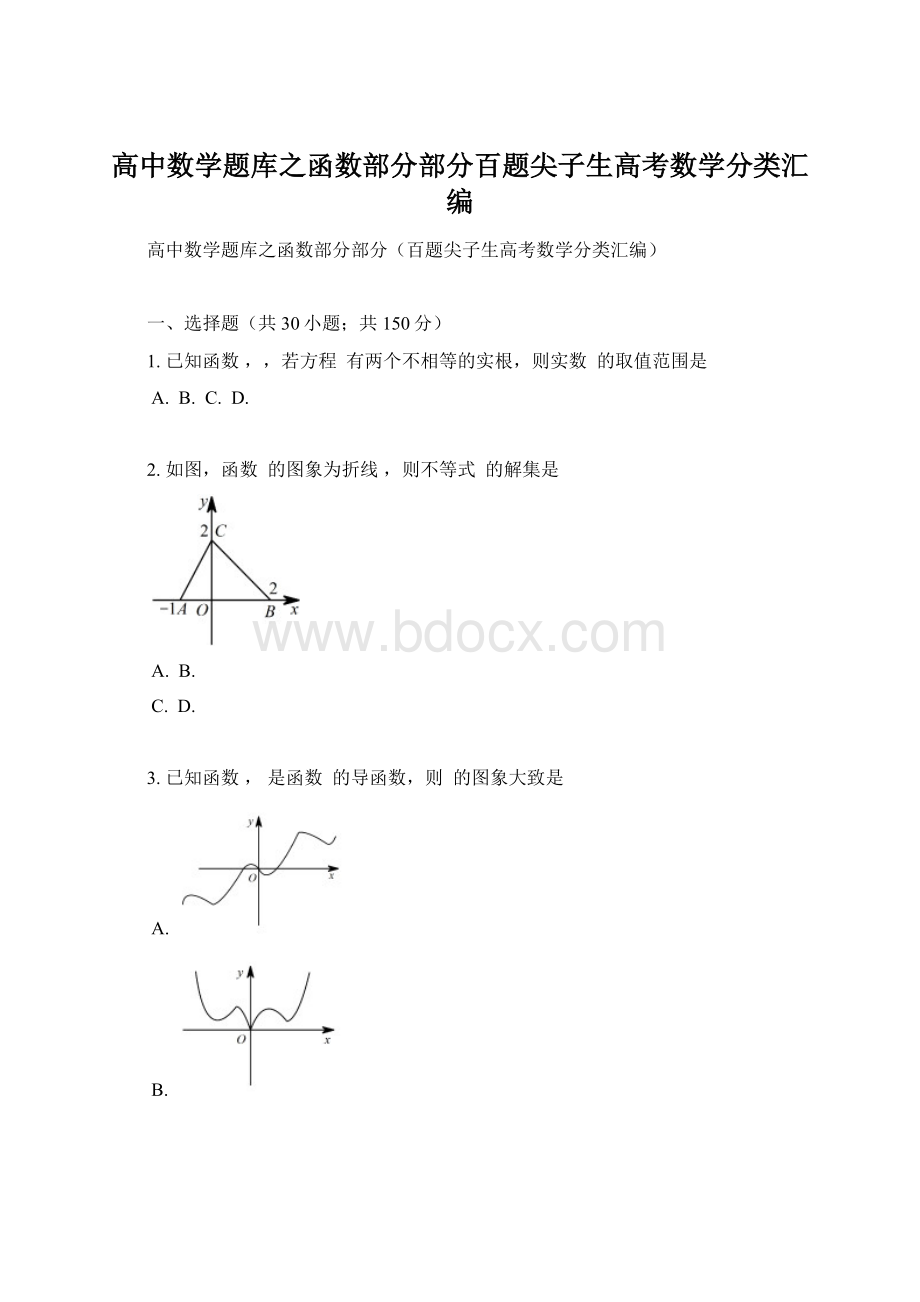
③当时，

则函数在区间上的零点个数为

15.设，若函数在区间上有三个零点，则实数的取值范围是

16.设是定义在上的恒不为零的函数，对任意实数，都有，若，，则数列的前项和的取值范围是

17.已知函数，则的值为

18.已知函数，则的值为

19.设是定义在上的偶函数，对任意，都有，且当时，，若在区间内关于的方程恰有个不同的实数根，则的取值范围是

20.已知函数函数．若函数恰好有个不同零点，则实数的取值范围是

21.已知函数的定义域为，若存在常数，对任意，有，则称为函数．给出下列函数：

①；

②；

③；

④；

⑤是定义在上的奇函数，且满足对一切实数均有．其中是函数的序号为

A.①②④B.②③④C.①④⑤D.①②⑤

22.已知函数，点，是函数图象上不同两点，则（为坐标原点）的取值范围是

23.已知函数（且）在上单调递增，且，则的取值范围为

24.已知是定义在上的函数的导函数，若方程无解，且，，设，，，则，，的大小关系是

25.已知函数（，且）在上单调递减，且关于的方程恰好有两个不相等的实数解，则的取值范围是

26.已知，都是定义在上的函数，且满足以下条件：

①（，且）；

③．若，则等于

A.B.C.D.或

27.函数在上有定义，若对任意，有，则称在上具有性质．设在上具有性质，现给出如下命题：

①在上的图象是连续不断的；

②在上具有性质；

③若在处取得最大值，则，；

④对任意，有．

其中真命题的序号是

A.①②B.①③C.②④D.③④

28.设函数（，为自然对数的底数），若曲线上存在点使得，则的取值范围是

29.设函数是奇函数的导函数，，当时，，则使得成立的的取值范围是

30.过双曲线的一个焦点作平行于渐近线的两直线，与双曲线分别交于两点，若，则双曲线离心率的值所在区间是

二、填空题（共30小题；

31.把下面不完整的命题补充完整，并使之成为真命题：

若函数的图象与的图象关于 

对称，则函数 

（填上你认为可以成为真命题的一种情形即可，不必考虑所有可能的情形）．

32.已知函数若函数有两个不同的零点，则实数的取值范围是 

．

33.已知函数，其中．若存在实数，使得关于的方程有三个不同的根，则的取值范围是 

34.已知，若函数有三个不同的零点，，，则的取值范围是 

35.在平面直角坐标系中，把位于直线与直线（，均为常数，且）之间的点所组成的区域（含直线，直线）称为“型带状区域”，设为二次函数，三点，，均位于“型带状区域”，如果点位于“型带状区域”，那么，函数的最大值为 

36.已知函数在区间上有零点，则的最大值是 

37.已知函数，则不等式的解集为 

38.已知函数在区间内有两个零点，则的取值范围是 

39.若实数，，且，则当的最小值为时，函数的零点个数为 

40.如图，已知正方形的边长为，平行于轴，顶点，和分别在函数，和的图象上，则实数的值为 

41.定义在上的函数满足，，则等于 

42.函数是定义在上的偶函数，且满足．当时，．若在区间上方程恰有四个不相等的实数根，则实数的取值范围是 

43.设各项均为正数的数列的前项之积为，若，则数列中最小项的序号 

44.已知点，，且平行四边形的四个顶点都在函数的图象上，则四边形的面积为 

45.函数的定义域为实数集，，对于任意都有，若在区间内函数恰有三个不同的零点，则实数的取值范围是 

46.已知函数，当时，关于的方程的所有解的和为 

47.函数．

①.当时，函数的零点个数是 

；

②.若函数有两个不同的零点，则的取值范围是 

48.已知是有序数对集合上的一个映射，正整数数对在映射下的象为实数，记作．对于任意的正整数，映射由下表给出：

则 

，使不等式成立的的集合是 

49.对于函数，若存在区间，使得，则称函数具有性质，给出下列个函数：

③

其中具有性质的函数是 

（填入所有满足条件函数的序号）．

50.在平面直角坐标系中，若直线与曲线有四个公共点，则实数的取值范围是 

51.已知函数，若函数有三个不同的零点，，，且，则的取值范围是 

52.定义，设，，则的最小值为 

，当取到最小值时， 

， 

53.已知函数由下表给出

其中等于在中所出现的次数．则 

54.已知是定义在上的函数，且，则函数在区间上的零点的个数为 

55.已知函数的定义域是，关于函数给出下列命题：

①对于任意，函数是上的减函数；

②对于任意，函数存在最小值；

③存在，使得对于任意的，都有成立；

④存在，使得函数有两个零点．

其中正确命题的序号是 

．（写出所有正确命题的序号）．

56.已知正数满足：

，，则的取值范围是 

57.若是偶函数，则 

58.若函数对任意实数，在闭区间上总存在两实数，，使得成立，则实数的最小值为 

59.对于实数和，定义运算"

"

：

设，且关于的方程恰有三个互不相等的实数根，，，则的取值范围是 

60.已知，是非零不共线的向量，设，定义点集．当时，若对于任意的，不等式恒成立，则实数的最小值为 

三、解答题（共40小题；

共520分）

61.已知函数．

（1）证明：

函数是奇函数；

（2）求的单调区间．

62.已知二次函数为偶函数，，．关于的方程有且仅有一根．

（1）求，，的值；

（2）若对任意的，恒成立，求实数的取值范围；

（3）令，若存在使得，求实数的取值范围．

63.已知．

（1）当时，求的值域；

（2）设，当时，对任意，，总有成立，求的取值范围．

64.已知是定义在上的单调递增函数．对于任意的正数、满足；

对于满足．

（1）求；

（2）若，解不等式；

（3）求证：

65.已知平面内一动点与两定点和连线的斜率之积等于．

（1）求动点的轨迹的方程；

（2）设直线与轨迹交于，两点，线段的垂直平分线交轴于点，当变化时，求面积的最大值．

66.已知椭圆经过点，离心率为，点为椭圆的右顶点，直线与椭圆相交于不同于点的两个点，．

（1）求椭圆的标准方程；

（2）当时，求面积的最大值；

（3）若，求证：

为定值．

67.已知椭圆经过点，离心率为，点为椭圆的右顶点，直线与椭圆相交于不同于点的两个点，．

（3）若直线的斜率为，求证：

的外接圆恒过一个异于点的定点．

68.已知双曲线的焦距为，其中一条渐近线的方程为．以双曲线的实轴为长轴，虚轴为短轴的椭圆记为，过原点的动直线与椭圆交于，两点．

（1）求椭圆的方程；

（2）若点为椭圆的左顶点，，求的取值范围；

（3）若点满足，求证为定值．

69.已知椭圆：

的离心率为，其右焦点为．

（2）若，，，四点都在椭圆上，已知与共线，与共线，且，求四边形的面积的最小值和最大值．

70.已知函数，对任意实数，都有成立．

（1）求函数所有零点之和；

（2）对任意实数，函数恒成立，求实数的取值范围．

71.已知函数（是常数，）．

（1）若是函数的极值点，求曲线在点处的切线方程；

（2）当时，方程在上有两解，求实数的取值范围；

，．

72.已知函数和.

（1）当时，求方程的实根；

（2）若对于任意的，恒成立，求的取值范围；

73.已知椭圆经过点，左右焦点分别为，，圆与直线相交所得弦长为．

（2）设是椭圆上不在轴上的一个动点，为坐标原点，过点作的平行线交椭圆于，两个不同的点，求的取值范围．

74.已知椭圆，，分别是其左、右焦点，以为直径的圆与椭圆有且仅有两个交点．

（2）设过点且不与坐标轴垂直的直线交椭圆于，两点，线段的垂直平分线与轴交于点，点横坐标的取值范围是，求线段长的取值范围．

75.如图，已知圆，是圆上的点，点在线段上，且有点和上的点，满足，．

（1）当在圆上运动时，求点的轨迹方程；

（2）若斜率为的直线与（）中所求的轨迹交于不同两点，，又点，求面积最大时对应的直线的方程．

76.已知椭圆的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线与以椭圆的右焦点为圆心，以椭圆的长半轴长为半径的圆相切．

（2）过点的直线与椭圆相交于不同的两点和，若椭圆上存在点满足（其中为坐标原点），求实数的取值范围．

77.已知是公差为的等差数列，是公比为的等比数列，，正整数组．

（1）若，求的值；

（2）若数组中的三个数构成公差大于的等差数列，且，求的最大值；

（3）若，，试写出满足条件的一个数组和对应的通项公式．（注：

本小问不必写出解答过程）

78.设函数．

（1）若函数是奇函数，求实数的值；

（2）若对任意的实数，函数（，为实常数）的图象与函数的图象总相切于一个定点．

①求与的值；

②对上的任意实数，，都有，求实数的取值范围．

79.如图，半圆是某爱国主义教育基地一景点的平面示意图，半径的长为百米．为了保护景点，基地管理部门从道路上选取一点，修建参观线路，且，，均与半圆相切，四边形是等腰梯形，设百米，记修建每百米参观线路的费用为万元，经测算．

（1）用表示线段的长；

（2）求修建参观线路的最低费用．

80.对于定义域为的函数，如果同时满足：

①对任意的，总有；

③若，，，都有成立，则称函数为理想函数．

（1）若函数为理想函数，证明：

（2）试判断函数，，是否是理想函数．

81.已知函数．曲线在点处的切线与轴交点的横坐标为．

（1）求的值；

（2）证明：

当时，曲线与直线只有一个交点．

82.设函数．

（1）求函数的单调区间和极值；

（2）若函数在区间上存在唯一零点，求的取值范围．

83.已知函数，．

（1）当时，解不等式；

（2）若存在，使得成立，求实数的取值范围．

84.已知椭的离心率为，，是椭圆的两个焦点，是椭圆上任意一点，且的周长是．

（2）设圆，过椭圆的上顶点作圆的两条切线交椭圆于，两点，当圆心在轴上移动且时，求的斜率的取值范围．

85.已知．

（1）若，当时，求的最大值；

（2）对于任意的实数，都有一个最大的正数，使得当时，恒成立，求的最大值及相应的．

86.设，是的反函数．

（1）设关于的方程在区间上有实数解，求的取值范围；

（2）当（为自然对数的底数）时，证明：

（3）当时，试比较与的大小，并说明理由．

87.设函数，．

（1）当（为自然对数的底数）时，求的极小值；

（2）讨论函数零点的个数；

（3）若对任意，恒成立，求的取值范围．

88.已知函数，．

（参考数据，，取，，）

（1）若函数在上单调递减，求实数的取值范围；

（2）若有两个不同的零点，，试比较与的大小．

89.已知函数，．若对任意的恒成立．数列满足，．

（1）确定的解析式；

（3）设为数列的前项和，求证：

90.设二次函数，其图象过点，且与直线有交点．

（1）求证：

（2）若直线与函数的图象从左到右依次交于，，，四点，若线段，，能构成钝角三角形，求的取值范围．

91.已知定义在上的偶函数，当时，．

（1）当时，求过原点与函数图象相切的直线的方程；

（2）求最大的整数，使得存在，只要，就有．

92.对于函数，若时，恒有成立，则称函数是上的函数．

（1）当函数是定义域上的函数时，求的取值范围；

（2）若函数为上的函数，①试比较与的大小；

②求证：

对于任意大于的实数，，，，，均有．

93.对于数对序列，记，

，其中为不超过的最大整数．（注：

表示当取时，中的最大数）

已知数对序列，回答下列问题：

（1）写出的值

（2）求的值，以及此时的的值；

（3）求得的值时，得到，，，试写出的取值范围．（只需写出结论，不用说明理由）

94.已知函数，（其中，且为常数．）

（1）若对于任意的，都有成立，求的取值范围；

（2）在1的条件下，若方程在上有且只有一个实根，求的取值范围．

95.已知函数．

（1）若直线与的反函数的图象相切，求实数的值；

（2）设，讨论曲线与曲线公共点的个数；

（3）设，比较与的大小，并说明理由．

96.已知函数，．

（1）当为何值时，轴为曲线的切线；

（2）用表示，中的最小值，设函数，讨论零点的个数．

97.已知常数，数列满足，．

（1）若，，①求的值；

②求数列的前项和；

（2）若数列中存在三项，，（，）依次成等差数列，求的取值范围．

98.考查函数在其定义域内的单调性情况：

若在内呈先减再增，则称为“型”函数；

若在内呈减-增-减-增，则称为“型”函数．给定函数．

（1）试写出这样的一个实数对，使函数为上的"

型"

函数，且为上的"

函数．（写出你认为正确的一个即可，不必证明）

（2）若为上的“型”函数，若存在实数，使与能同时成立，求实数的取值范围．

99.已知函数，，其中．设．

（1）若在处取得极值，且，求函数的单调区间；

（2）若时，函数有两个不同的零点，．

①求的取值范围；

②求证：

100.已知函数，其中且．

（1）讨论的单调性；

（2）若不等式恒成立，求实数的取值范围；

（3）若方程存在两个异号实根，，求证：

答案

第一部分

1.B【解析】画出函数的图象，如图所示．

若方程有两个不相等的实根，则函数，有两个交点，此时，直线只有夹在两条虚线之间才有两交点．故，且．

2.C【解析】方法一：

由图象可得，所以等价于或

当时，，则所以．

当时，令，，则由，得．

结合函数的单调性（该函数在定义域上单调递减）知．

综上，原不等式的解集为．

方法二：

令，作出的图象，如图．

当时，，又，所以由，得．

3.A【解析】，它是奇函数，可排除B、D；

考察函数与的图象，它们有个交点，可排除C．

4.A【解析】设年平均增长率为，则第年到第年，有，所以，当的比值越大时，年平均增长率最高，由图可知，从第一年到第三年的年平均增长率最高．

5.C

【解析】对于任意，总存在，

使得成立，

即函数的值域是函数值域的子集，，

令，则函数单调递增，

所以，

于是有；

单调递增，

所以；

即

解得．

6.D【解析】．

由，得，解得．

由在内没有零点，得，

解得，

因此，．

7.C【解析】1）当时，，此时，成立．

2）当时，．

当，即时，，成立．

当，即时，，此时，所以不满足题意．

综上，的取值范围是．

8.D9.B10.C

【解析】当时，

函数的图象为开口向下的抛物线，所以在时，不恒成立．

函数当时，．

所以不满足题意．

当时，，，不满足题意．

当时，

需在时恒成立，

所以令或

即或

解得或．综合得：

11.D【解析】作出函数的图象，如图，

要使成立，则必有．当时，，则与相等时，满足条件．

由，

，

所以．

12.A【解析】由题意，，因为是开口朝上的二次函数，所以，得由此可画出可行域，如图，

表示可行域内的点和点连线的斜率，显然的斜率最小，的斜率最大．

13.B【解析】函数的对称轴为，且在区间上是减函数，得，对任意的，总有恒成立，即，又，当时，，，所以，又，所以的取值范围是．

14.A【解析】由得函数的图象关于点对称，由得函数的图象关于直线对称，作出函数在区间上的图象，再由对称性作出函数在区间上的图象，并在同一坐标系内作出函数的图象，由图象可知函数在区间上有个零点．

15.D

【解析】函数在区间上有三个零点即函数与在区间上有三个交点．画图如下．

当时，显然，不合乎题意，当时，由图知，当时，存在一个交点，当时，，可得，，若，可得，为减函数，若，可得，为增函数，此时与必须在上有两个交点，即在上有两个零点，所以解得，故函数在区间上有三个零点时