高中物理必修二知识点总结(人教版).wps
《高中物理必修二知识点总结(人教版).wps》由会员分享,可在线阅读,更多相关《高中物理必修二知识点总结(人教版).wps(39页珍藏版)》请在冰豆网上搜索。
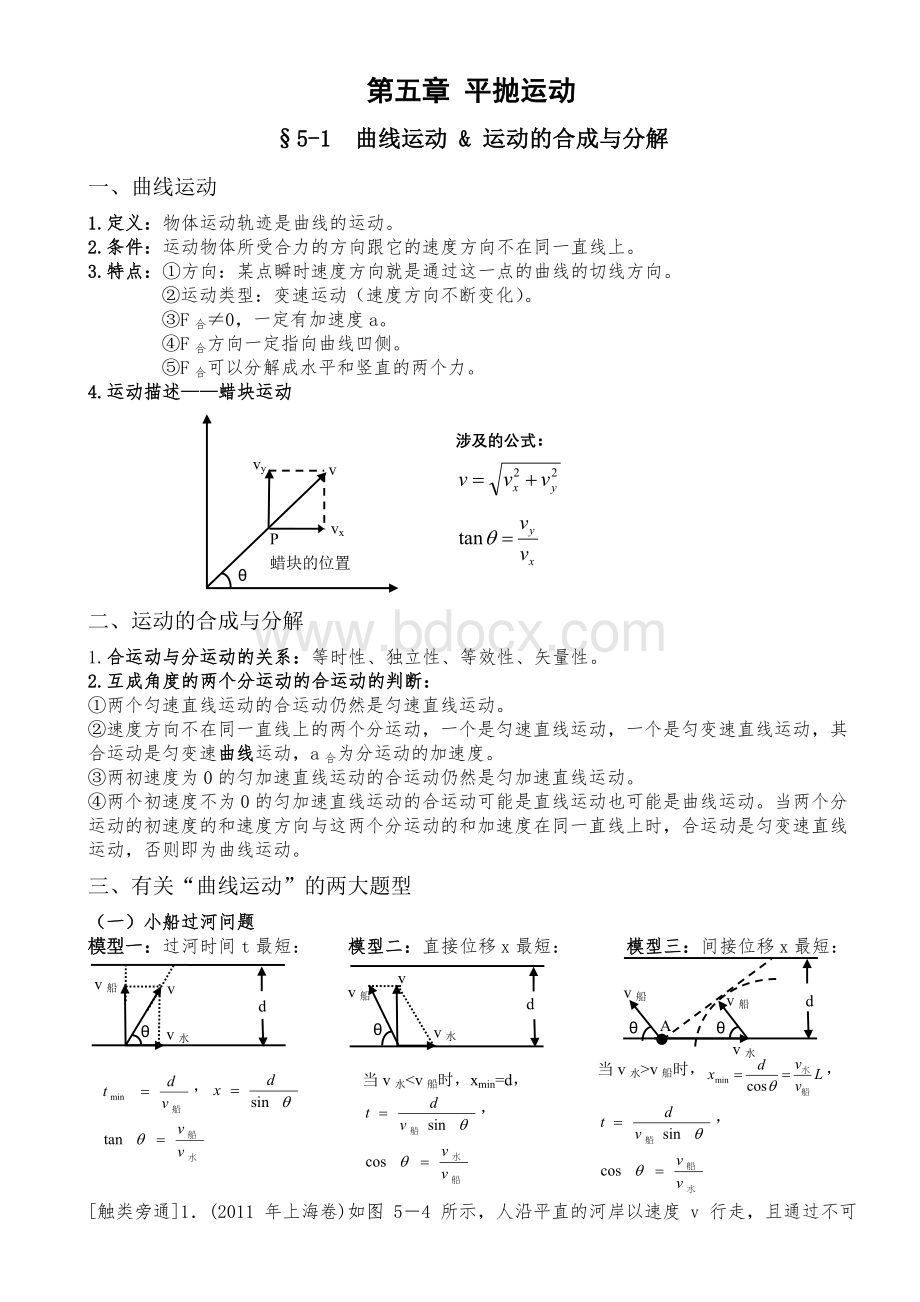
P蜡块的位置vvxvy涉及的公式:
22yxvvvxyvvtanvv水v船船vdtmin,sindx水船vvtand第五章平抛运动第五章平抛运动5-1曲线运动&运动的合成与分解5-1曲线运动&运动的合成与分解一、曲线运动1.定义:
1.定义:
物体运动轨迹是曲线的运动。
2.条件:
2.条件:
运动物体所受合力的方向跟它的速度方向不在同一直线上。
3.特点:
3.特点:
方向:
某点瞬时速度方向就是通过这一点的曲线的切线方向。
运动类型:
变速运动(速度方向不断变化)。
F合0,一定有加速度a。
F合方向一定指向曲线凹侧。
F合可以分解成水平和竖直的两个力。
4.运动描述蜡块运动4.运动描述蜡块运动二、运动的合成与分解1.合运动与分运动的关系:
合运动与分运动的关系:
等时性、独立性、等效性、矢量性。
2.互成角度的两个分运动的合运动的判断:
2.互成角度的两个分运动的合运动的判断:
两个匀速直线运动的合运动仍然是匀速直线运动。
速度方向不在同一直线上的两个分运动,一个是匀速直线运动,一个是匀变速直线运动,其合运动是匀变速曲线曲线运动,a合为分运动的加速度。
两初速度为0的匀加速直线运动的合运动仍然是匀加速直线运动。
两个初速度不为0的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。
当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时,合运动是匀变速直线运动,否则即为曲线运动。
三、有关“曲线运动”的两大题型
(一)小船过河问题
(一)小船过河问题模型一:
模型一:
过河时间t最短:
模型二:
模型二:
直接位移x最短:
模型三:
模型三:
间接位移x最短:
触类旁通1(2011年上海卷)如图54所示,人沿平直的河岸以速度v行走,且通过不可dvv水v船当v水v船时,Lvvdx船水cosmin,sin船vdt,水船vvcossin)cos-(min船船水vLvvsv船d伸长的绳拖船,船沿绳的方向行进此过程中绳始终与水面平行,当绳与河岸的夹角为时,船的速率为(C)。
sin.vAsin.vBcos.vCcos.vD解析:
解析:
依题意,船沿着绳子的方向前进,即船的速度总是沿着绳子的,根据绳子两端连接的物体在绳子方向上的投影速度相同,可知人的速度v在绳子方向上的分量等于船速,故v船vcos,C正确2(2011年江苏卷)如图55所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直,且OAOB.若水流速度不变,两人在静水中游速相等,则他们所用时间t甲、t乙的大小关系为(C)At甲t乙D无法确定解析:
解析:
设游速为v,水速为v0,OAOBl,则t甲lvv0lvv0;乙沿OB运动,乙的速度矢量图如图4所示,合速度必须沿OB方向,则t乙2lv2v20,联立解得t甲t乙,C正确
(二)绳杆问题(连带运动问题)
(二)绳杆问题(连带运动问题)1、实质:
合运动的识别与合运动的分解。
2、关键:
物体的实际运动是合速度,分速度的方向要按实际运动效果确定;沿绳(或杆)方向的分速度大小相等。
模型四:
模型四:
如图甲,绳子一头连着物体B,一头拉小船A,这时船的运动方向不沿绳子。
处理方法:
处理方法:
如图乙,把小船的速度vA沿绳方向和垂直于绳的方向分解为v1和v2,v1就是拉绳的速度,vA就是小船的实际速度。
触类旁通如图,在水平地面上做匀速直线运动的汽车,通过定滑轮用绳子吊起一个物体,若汽车和被吊物体在同一时刻的速度分别为v1和v2,则下列说法正确的是(C)A物体做匀速运动,且v2v1B物体做加速运动,且v2v1BOOAvAv1v2vA甲乙C物体做加速运动,且v2v1D物体做减速运动,且v2r,联立式解得r4743gv20.5-3圆周运动&向心力&生活中常见圆周运动5-3圆周运动&向心力&生活中常见圆周运动一、匀速圆周运动1.定义:
1.定义:
物体的运动轨迹是圆的运动叫做圆周运动,物体运动的线速度大小不变的圆周运动即为匀速圆周运动。
2.特点:
2.特点:
轨迹是圆;线速度、加速度均大小不变,方向不断改变,故属于加速度改变的变速曲线运动,匀速圆周运动的角速度恒定;匀速圆周运动发生条件是质点受到大小不变、方向始终与速度方向垂直的合外力;匀速圆周运动的运动状态周而复始地出现,匀速圆周运动具有周期性。
3.描述圆周运动的物理量:
3.描述圆周运动的物理量:
考点一:
沿初速度方向的水平位移:
根据mamgatbtvssin,21,20.sin20gbvs考点二:
入射的初速度:
.2sin,21,sinsin002bgvtvatabgmmga考点三:
P到Q的运动时间:
.sin2,21,sinsin2gbttabgmmga
(1)线速度v线速度v是描述质点沿圆周运动快慢的物理量,是矢量;其方向沿轨迹切线,国际单位制中单位符号是m/s,匀速圆周运动中,v的大小不变,方向却一直在变;
(2)角速度角速度是描述质点绕圆心转动快慢的物理量,是矢量;国际单位符号是rads;(3)周期T周期T是质点沿圆周运动一周所用时间,在国际单位制中单位符号是s;(4)频率f频率f是质点在单位时间内完成一个完整圆周运动的次数,在国际单位制中单位符号是Hz;(5)转速n转速n是质点在单位时间内转过的圈数,单位符号为r/s,以及r/min4.各运动参量之间的转换关系:
4.各运动参量之间的转换关系:
.2,2222RvTnTRvnRRTRv变形5.三种常见的转动装置及其特点:
5.三种常见的转动装置及其特点:
模型一:
模型一:
共轴传动模型二:
模型二:
皮带传动模型三:
模型三:
齿轮传动触类旁通1、一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则(AC)AA球的角速度必小于B球的角速度BA球的线速度必小于B球的线速度CA球的运动周期必大于B球的运动周期DA球对筒壁的压力必大于B球对筒壁的压力解析:
解析:
小球A、B的运动状态即运动条件均相同,属于三种模型中的皮带传送。
则可以知道,两个小球的线速度v相同,B错;因为RARB,则AB,TATB,A.C正确;又因为两小球各方面条件均相同,所以,两小球对筒壁的压力相同,D错。
所以A、C正确。
2、两个大轮半径相等的皮带轮的结构如图所示,AB两点的半径之比为2:
1,CD两点的半径之比也为2:
1,则ABCD四点的角速度之比为1122,这四点的线速度之比为2142。
二、向心加速度1.定义:
1.定义:
任何做匀速圆周运动的物体的加速度都指向圆心,这个加速度叫向心加速度。
注:
并不是任何情况下,向心加速度的方向都是指向圆心。
当物体做变速圆周运动时,向心加速度的一个分加速度指向圆心。
2.方向:
2.方向:
在匀速圆周运动中,始终指向圆心,始终与线速度的方向垂直。
向心加速度只改变线rROBABABABATTrRvv,ABOrROrRTTRrvvABABBA,ABr2r1ABBABAnnrrTTvv2121,速度的方向而非大小。
3.意义:
3.意义:
描述圆周运动速度方向方向改变快慢的物理量。
4.公式:
4.公式:
.)2(22222rnrTvrrvan5.两个函数图像:
5.两个函数图像:
触类旁通1、如图所示的吊臂上有一个可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩。
在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起。
A、B之间的距离以d=H2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化。
对于地面的人来说,则物体做(AC)速度大小不变的曲线运动速度大小增加的曲线运动加速度大小方向均不变的曲线运动加速度大小方向均变化的曲线运动2、如图所示,位于竖直平面上的圆弧轨道光滑,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,到达B点时的速度为,最后落在地面上C点处,不计空气阻力,求:
(1)小球刚运动到B点时的加速度为多大,对轨道的压力多大;
(2)小球落地点C与B点水平距离为多少。
三、向心力1.定义:
1.定义:
做圆周运动的物体所受到的沿着半径指向圆心的合力,叫做向心力。
2.方向:
2.方向:
总是指向圆心。
3.公式:
3.公式:
.)2(22222rnmrTmmvrmrvmFn4.几个注意点:
4.几个注意点:
向心力的方向总是指向圆心,它的方向时刻在变化,虽然它的大小不变,但是向心力也是变力。
在受力分析时,只分析性质力,而不分析效果力,因此在受力分析是,不要加上向心力。
描述做匀速圆周运动的物体时,不能说该物体受向心力,而是说该物体受到什么力,这几个力的合力充当或提供向心力。
OOananrrv一定一定AB四、变速圆周运动的处理方法1.特点:
1.特点:
线速度、向心力、向心加速度的大小和方向均变化。
2.动力学方程:
2.动力学方程:
合外力沿法线方向的分力提供向心力:
rmrvmFn22。
合外力沿切线方向的分力产生切线加速度:
FT=maT。
3.离心运动:
3.离心运动:
(1)当物体实际受到的沿半径方向的合力满足F供=F需=m2r时,物体做圆周运动;当F供F需=m2r时,物体做离心运动。
(2)离心运动并不是受“离心力”的作用产生的运动,而是惯性的表现,是F供gR小球固定在轻杆的一端在竖直平面内转动杆对球可以是拉力也可以是支持力若F0,则mgmv2R,vgR若F向下,则mgFmv2R,vgR若F向上,则mgFmv2R或mgF0,则0vgR小球在竖直细管内转动管对球的弹力FN可以向上也可以向下依据mgmv20R判断,若vv0,FN0;若vv0,FN向下球壳外的小球在最高点时弹力FN的方向向上如果刚好能通过球壳的最高点A,则vA0,FNmg如果到达某点后离开球壳面,该点处小球受到壳面的弹力FN0,之后改做斜抛运动,若在最高点离开则为平抛运动六、有关生活中常见圆周运动的涉及的几大题型分析
(一)解题步骤:
(一)解题步骤:
明确研究对象;定圆心找半径;对研究对象进行受力分析;对外力进行正交分解;列方程:
将与和物体在同一圆周运动平面上的力或其分力代数运算后,另得数等于向心力;解方程并对结果进行必要的讨论。
(二)典型模型:
(二)典型模型:
I、圆周运动中的动力学问题谈一谈:
谈一谈:
圆周运动问题属于一般的动力学问题,无非是由物体的受力情况确定物体的运动情况,或者由物体的运动情况求解物体的受力情况。
解题思路就是,以加速度为纽带,运用那个牛顿第二定律和运动学公式列方程,求解并讨论。
模型一:
模型一:
火车转弯问题:
模型二:
模型二:
汽车过拱桥问题:
触类旁通1、铁路在弯道处的内外轨道高度是不同的,已知内外轨道平面与水平面的倾角为,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度小于,则(A)A内轨对内侧车轮轮缘有挤压B外轨对外侧车轮轮缘有挤压C这时铁轨对火车的支持力等于D这时铁轨对火车的支持力大于解析:
解析:
当内外轨对轮缘没有挤压时,物体受重力和支持力的合力提供向心力,此时速度为gRtan。
2、如图所示,质量为m的物体从半径为R的半球形碗边向碗底滑动,滑倒FNF合mghLa、涉及公式:
LhmgmgFsinmgtan合RvmF20合,由得:
LRghv0。
b、分析:
设转弯时火车的行驶速度为v,则:
(1)若vv0,外轨道对火车轮缘有挤压作用;
(2)若vv0,内轨道对火车轮缘有挤压作用。
a、涉及公式:
RvmFmgN2,所以当mgRvmmgFN2,此时汽车处于失重状态,而且v越大越明显,因此汽车过拱桥时不宜告诉行驶。
b、分析:
当gRvRvmmgFN2:
(1)gRv,汽车对桥面的压力为0,汽车出于完全失重状态;
(2)gRv0,汽车对桥面的压力为mgFN0。
(3)gRv,汽车将脱离桥面,出现飞车现象。
c、注意:
同样,当汽车