力学压轴题文档格式.docx

力学压轴题文档格式.docx

《力学压轴题文档格式.docx》由会员分享，可在线阅读，更多相关《力学压轴题文档格式.docx（22页珍藏版）》请在冰豆网上搜索。

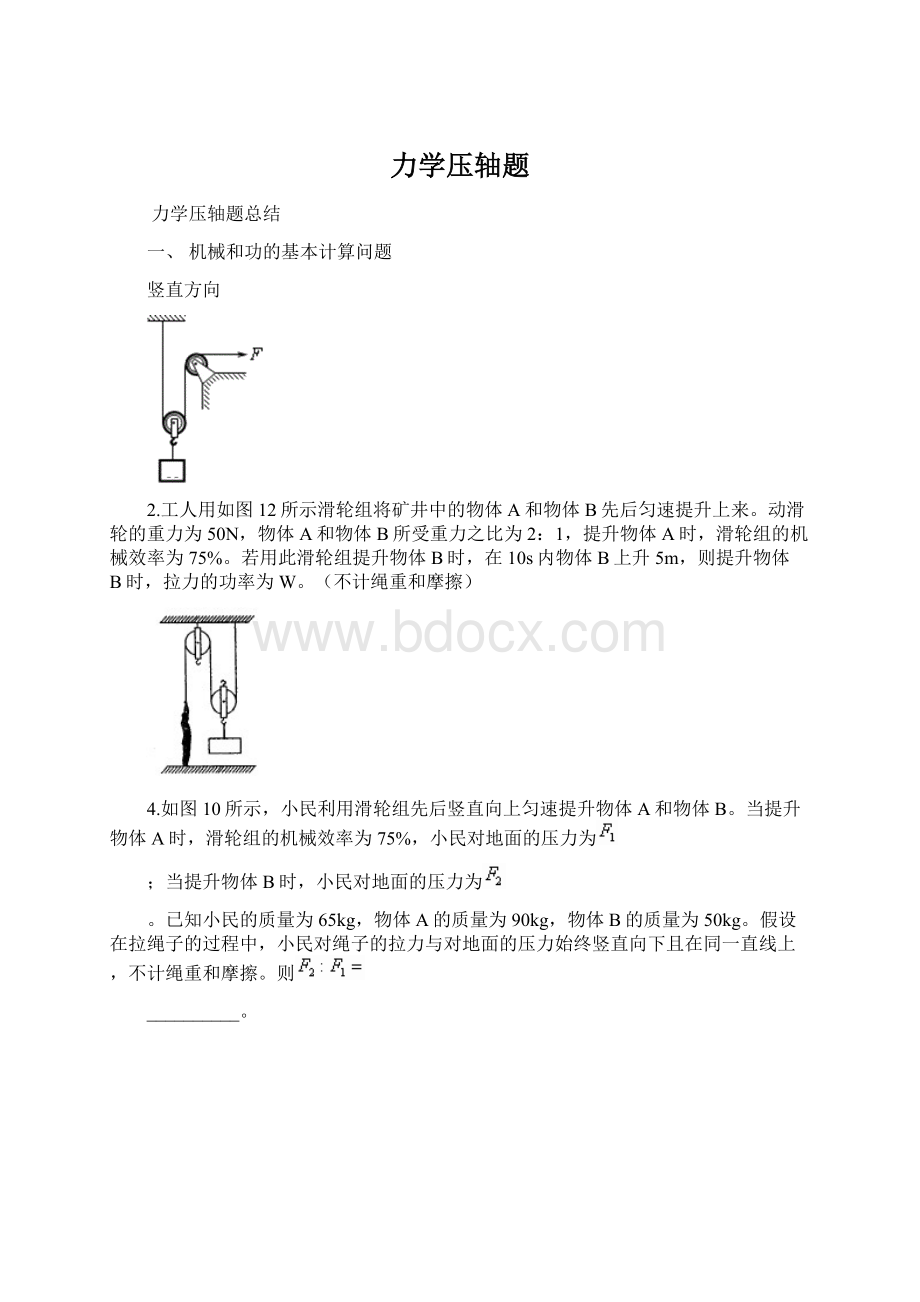
水平方向

4.用图7所示的滑轮组拉物体A在水平桌面上做匀速直线运动。

如果拉力F＝3N，物体A的速度v＝0.2m/s，忽略滑轮重、绳重和轴摩擦。

下列说法中正确的是

A．物体A受到合力不为零B．物体A受到的拉力为9N

C．竖直墙受到的拉力为9ND．拉力F每秒钟做功为1.8J

5.如图7所示，每个滑轮均重12N，用滑轮组拉着重600N的物体A沿水平方向匀速移动，在40s内物体移动了8m，拉力F做的功为1280J．（不计绳重及机械内部摩擦）

A．拉力F的大小60NB．滑轮组对物体A所做的有用功为1184J

C．拉力F的功率32WD.滑轮组的机械效率为72.5%

7.如图所示，滑轮组在拉力F1的作用下，拉着重500N的物体A以0.2m/s的速度在水平面上匀速直线移动，滑轮组的机械效率为80%，物体A运动时受的阻力为56N，拉力F1的功率为P1，在10s内拉力做功为W1。

若滑轮组在拉力为F2的作用下，拉着物体A以0.5m/s的速度在此水平面上匀速直线移动，拉力F2的功率为P2，在20s内拉力做功为W2。

滑轮自重和绳重忽略不计，则

A．F1＝168NW1＝112J

B．F1＝210NW1＝140J

C．F2＝210NW2＝700J

D．P1＝14WP2＝35W

二、机械和功与摩擦力相结合的问题

（08ftym）

（08sjsym）

（09xwym）

三、机械和功与几次压强变化问题（关键找压强变化的原因）

40．图25是液压汽车起重机从水中打捞重物的示意图。

A是动滑轮，B是定滑轮，C是卷扬机，D是油缸，E是柱塞。

作用在动滑轮上共三股钢丝绳，卷扬机转动使钢丝绳带动动滑轮上升提取重物，被打捞的重物体积V＝0.5m3。

若在本次打捞前起重机对地面的压强p0＝2.0×

107Pa，当物体在水中匀速上升时起重机对地面的压强p1＝2.375×

107Pa，物体完全出水后起重机对地面的压强p2＝2.5×

107Pa。

假设起重时柱塞沿竖直方向，物体出水前、后柱塞对吊臂的支撑力分别为N1和N2，N1与N2之比为19：

24。

重物出水后上升的速度v＝0.45m/s。

吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计。

（g取10N/kg）求：

（1）被打捞物体的重力；

（2）被打捞的物体浸没在水中上升时，滑轮组AB的机械效率；

（3）重物出水后，卷扬机牵引力的功率。

解：

（1）设起重机重为G，被打捞物体重力为G物；

　　　　打捞物体前，　　　　　G=p0S

　　　　在水中匀速提升物体时：

F拉=G物－F浮

　　　　起重机对地面的压力：

　G+F拉=p1S

　　　　　　　　　　　　　　　F浮=ρ水gV排=0.5×

104N

　　　　物体出水后：

G+G物=p2S

　　　　　　　　　　F拉=（p1-p0）S；

　　　　　　　　　　G物=（p2-p0）S

　　　　可得物体重力为　　G物=2.0×

104N。

（2）设钢丝绳上的力在出水前后分别为F1、F2，柱塞对吊臂力的力臂为L1，

　　　　钢丝绳对吊臂力的力臂为L2。

根据杠杆平衡条件可知：

　　　　N1L1=3F1L2；

N2L1=3F2L2

=

　　　　F1=

（G物－F浮+G动），F2=

（G物+G动）

=

　=

　　　　将数据代入得：

G动=0.4×

　　　　物体浸没在水中上升时，滑轮组AB的机械效率：

　　（3）出水后钢丝绳上的力：

F2=（G物+G动）/3=0.8×

　　　　物体上升的速度为v，则钢丝绳的速度：

v＇=3v=3

0.45m/s=1.35m/s

　　　　　　　　　　　　　　　　　　　　　　P=F2v＇=0.8×

104N×

1.35m/s=1.08×

104W。

39．图22是液压汽车起重机从水中打捞重物的示意图。

起重机总重G＝8×

104N，A是动滑轮，B是定滑轮，C是卷扬机，D是油缸，E是柱塞。

通过卷扬机转动使钢丝绳带动A上升，打捞体积V＝0.5m3、重为G物的重物。

若在打捞前起重机对地面的压强p1＝2×

107Pa，当物体在水中匀速上升时起重机对地面的压强为p2，重物完全出水后匀速上升时起重机对地面的压强p3＝2.5×

假设起重时E沿竖直方向，重物出水前、后E对吊臂的支撑力分别为N1和N2，重物出水前滑轮组的机械效率为80%，重物出水后卷扬机牵引力的功率为11875W，吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计。

（1）重物在水中匀速上升时起重机对地面的压强p2；

（2）支撑力N1和N2之比；

（3）重物出水后匀速上升的速度。

与杠杆相关的压强变化问题

2.轻质硬杆AB长75cm。

用长短不同的线把边长为10cm的立方体甲和体积是1dm3的球乙分别拴在杆的AB两端。

在距A点30cm处的O点支起AB时，甲静止在桌面上，乙悬空，杆AB处于水平平衡。

将乙浸没在水中后，杆AB仍平衡，如图10所示。

此时甲对水平桌面的压强改变了___________Pa。

（取g＝10N/kg）

（08cwym）37.如图25所示是起重机的结构示意图。

用它把质量为2×

103kg，底面积为1m2的货箱G匀速提起。

（取g＝10N/kg）已知：

OA＝10m，OB＝5m。

（设起重机所受重力的作用线恰好通过O点。

）问：

（1）当货箱静止于水平地面时，它对地面的压强是多少？

（2）若把货箱匀速吊起3m，起重机对货箱做了多少功？

（3）吊起货箱时，为使起重机不倾倒，在它右边加挂质量为多大的铁块？

（08ftym）42．如图24所示的装置，O为杠杆AC的支点，OA:

OC=1:

2，在杠杆的A点挂一边长为0.2m的立方体D，在杠杆上B点作用竖直向下的拉力F，当杠杆在水平位置平衡时，物体D对地面的压强p1为7000Pa，A点受到向下的拉力为F1´

在杠杆上C点作用竖直向下的拉力F，当杠杆在水平位置平衡时，物体D对地面的压强p2为6000Pa，A点受到向下的拉力为F2´

，OB:

BC=1:

2，杠杆和绳的质量忽略不计。

求

（1）F1´

和F2´

的比值；

（2）F的大小；

（3）如果要使物体D对地面的压强刚好为零，则人需要在C点用多大的力F´

（08cyym）37．图23是简易电动门式起重机的结构示意图。

MN为质量可以不计、长4m的横梁，行走装置可以把提起的重物在横梁上左右移动。

提升电动机通过钢丝绳和滑轮组提起重物，滑轮组的结构如图。

当提起的重物质量是0.5t，钢丝绳重和轮、轴间摩擦不计时，滑轮组的机械效率是80%。

当以0.2m/s的速度匀速竖直向上提起1.125t重物时，滑轮组的机械效率是多少？

电动机拉动钢丝绳的功率是多少？

若行走装置和提升电动机的总重是2.75×

103N，提起重物质量为2t，行走装置使提起的重物沿横梁从中点A移到B点，以M点为轴，N点向上的支持力增加了6×

103N，MB的距离是多少？

（g取10N/kg）（5分）

（09cyem）

（09cyym）39.火车与公路交叉处设置人工控制的栏杆，图22是栏杆的示意图。

栏杆全长AB=6m，在栏杆的左端安装配重，使栏杆和配重总体的重心位于O点。

栏杆的P点安装转轴，转轴与支架C连结，使栏杆能绕P在竖直平面无摩擦转动，支架C用两块木板做成，中间空隙可以容纳栏杆。

栏杆的B端搁置在支架D上，当支架D上受到压力为FD时，栏杆恰好在水平位置平衡。

当体重为G人的管理人员双脚站在水平地面时，他对地面的压强是p1；

当他用力F1竖直向下压A端，使栏杆的B端刚好离开支架，此时人双脚对地面的压强是p2。

管理人员继续用力可使栏杆逆时针转动至竖直位置，并靠在支架C上。

火车要通过时，他要在A端用力F2使栏杆由竖直位置开始离开支架C，使栏杆能顺时针转动直至栏杆B端又搁置在支架D上。

已知AP=OP=1m，PE=

m，O点到栏杆下边缘的距离OE=0.5m，p1∶p2=2∶1，栏杆与配重的总重G杆=240

N。

（1）FD

（2）G人

（3）F2的最小值，此时F2的方向。

（计算和结果可带根号）（6分）

（08cpym）37．（5分）（5分）如图30所示，一正方体合金块M的边长为20cm，把它挂在以O为支点的轻质杠杆的A点处，一个重为640N的人在杠杆的B点通过定滑轮用力F1使杠杆在水平位置平衡，此时M对水平地面的压强为1.1×

104Pa，人对水平地面的压强为1.45×

104Pa；

若把M浸没于水中（M与容器底不接触），人用力F2仍使杠杆在水平位置平衡，此时人对地面的压强为1.15×

104Pa；

已知人单独站在水平地面上，对地面的压强为1.6×

104Pa．（g取10N/kg）求：

（1）力F1的大小；

（2）合金块M的密度；

（3）当M浸没于水中时，若剪断细绳，合金块M沉于容器底，则M对容器底的压强为多大．

（09myym）

四、机械和功的比值问题

2．如图19所示，质量为70kg的工人站在水平地面上，用带有货箱的滑轮组把货物运到高出。

第一次运送货物时，放入货箱的货物质量为160kg，工人用F1匀速拉绳的功率为P1，货箱以0.1m/s的速度匀速上升，地面对工人的支持力为N1。

第二次运送货物时，放入货箱的货物质量为120kg，工人用力F2匀速拉绳，货箱以0.2m/s的速度匀速上升，地面对工人的支持力为N2，滑轮组机械效率为η2。

N1与N2之比为15:

19。

（1）货箱和动滑轮的总质量m；

（2）功率P1；

（3）机械效率η2。

5.如图是一个上肢力量健身器示意图。

配重A受到的重力为1200N，其底面积为5×

10－2m2.B、C都是定滑轮，D是动滑轮；

杠杆EH可绕O点在竖直平面内转动，OE：

0H＝2：

5。

小成受到的重力为600N，他通过细绳在H点施加竖直向下的拉力为T1时，杠杆在水平位置平衡，小成对地面的压力为F1，配重A受到的拉力为FA1，配重A对地面的P1为6×

103pa。

小成在H点施加竖直向下的拉力为T2时，杠杆仍在水平位置平衡，小成对地面的压力为F2，配重A受到的拉力为FA2，配重A对地面的压强P2为4×

已知F1：

F2＝20：

19，杠杆EH和细绳的质量均忽略不计。

求

（1）拉力FA2；

（2）拉力T2；

（3）动滑轮D受到的重力G。

（09cpym）39.如图24所示,质量为60kg的工人在水平地面上,用滑轮组把货物运到高处。

第一次运送货物时,货物质量为130kg,工人用力F1匀速拉绳,地面对工人的支持力为N1,滑轮组的机械效率为η1;

第二次运送货物时,货物质量为90kg,工人用力F2匀速拉绳的功率为P2,货箱以0.1m/s的速度匀速上升,地面对人的支持力为N2,N1与N2之比为2:

3。

（不计绳重及滑轮摩擦,g取10N/kg）

求:

（1）动滑轮重和力F1的大小;

（2）机械效率η1;

（3）功率P2。

（09fsym）

41.火车道口处设置人工控制的栏杆，图25是栏杆的示意图。

密度和粗细均匀的栏杆全长6m，质量为40kg。

栏杆的重心位于P点，栏杆可绕O点在竖直平面内无摩擦转动。

栏杆的H端通过滑轮组来提升栏杆，其中A、B、D、E、都是定滑轮，C是动滑轮,T为固定在水平地面上的挂钩。

当火车通过岔道口后,管理人员用力F1竖直向下拉绳子,栏杆恰好在水平位置平衡。

管理人员为了减轻自己的工作强度，他在H端下方的绳子上加挂了一个质量为10kg的重物，用力F2以0.2m/s的速度匀速拉动绳子使栏杆逆时针转动45°

角时车辆放行。

此时管理人员将绳端固定在挂钩T上。

已知：

F1∶F2＝17∶15；

OH=1m,忽略细绳与滑轮的摩擦。

g取10N/kg。

⑴动滑轮C的重力；

⑵F1的大小；

⑶F2的功率；

⑷管理人员用力F2工作时滑轮组的效率（结果保留一位小数）

五、机械和功与浮力相结合的问题

（09syym）6.某桥梁施工队的工人用如图24所示的滑轮组匀速打捞沉在水中的工件。

已知工件的质量为100kg工人的质量为70kg。

工件打捞出水面前与工件完全被打捞出水后工人对地面的压力之比为15：

2，工件在水中时，滑轮组的机械效率为60%。

若不计摩擦、绳重及水的阻力，g取10N/kg。

（1）工件浸没在水中时所受的浮力Ｆ浮；

（2）工件完全打捞出水面后，滑轮组的机械效率η2；

（3）工件完全打捞出水面后，以0.2m/s的速度被匀速提升，工人拉绳的功率P2。

（09hdym）38．如图23所示，质量为70kg的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材，该滑轮组中动滑轮质量为5kg。

当工人用120N的力拉滑轮组的绳端时，石材仍沉在水底不动。

工人继续增大拉力将石材拉起，在整个提升过程中，石材始终以0.2m/s的速度匀速上升。

在石材还没有露出水面之前滑轮组的机械效率为η1，当石材完全露出水面之后滑轮组的机械效率为η2。

在石材脱离水池底部至完全露出水面的过程中，地面对人的支持力的最大值与最小值之比为29：

21。

绳重及滑轮的摩擦均可忽略不计，石材的密度ρ石=2.5×

103kg/m3，取g=10N/kg，求：

（1）与打捞前相比，当人用120N的力拉绳端时，水池底部对石材的支持力变化了多少；

（2）η1与η2的比值；

（3）当石材完全露出水面以后，人拉绳子的功率。

（09cwym）34．小文的体重为600N，当他使用如图24所示的滑轮组匀速提升水中的体积为0.01m3的重物A时（重物始终未出水面），他对地面的压强为8.75×

103Pa。

已知小文与地面的接触面积为400

当他用此滑轮组在空气中匀速提升重物B时，滑轮组的机械效率是80%。

已知重物A重物B所受重力之比GA︰GB=5︰12，若不计绳重和摩擦，g=10N/kg。

（1）提升重物A时小文对地面的压力。

（2）物体A的密度。

（3）在水中提升重物A时滑轮组的机械效率。

（4）重物A完全出水面后，以0.2m/s的速度匀速上升，

小文拉绳的功率P。

六、

9.如图所示，湖水中有两艘小船，绳子的一端拴在甲船上，乙船上固定着滑轮，绳子绕过滑轮，站在甲船上的人用100N的力拉绳子的自由端。

如果在20s内甲船向右匀速移动了10m，同时乙船向左匀速移动了4m，则人对绳子的力做功的功率是

A.50WB.140WC.30WD.70W

2.在图所示装置中，甲物重G甲＝10N，乙物重G乙是动滑轮重G轮的8倍。

轻杆AB可以绕O点转动，且OA∶OB＝2∶1。

不计轴摩擦，装置如图所示处于平衡状态时，乙对水平地面的压力为30N。

（1）此时动滑轮对物体乙的拉力F拉；

（2）若在物体甲下面再加挂物体丙，恰使物体乙对地面的压力为零。

丙的物重G丙。

Ans：

F拉＝50N；

G丙＝5N

3.如图甲所示的滑轮组，每个滑轮等重。

不计绳重和摩擦，物体重G1从200N开始逐渐增加，直到绳子被拉断。

每次均匀速拉动绳子将物体提升同样的高度。

图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图像。

（1）每个滑轮重多少N?

（2）绳子能承受的最大拉力是多少N?

（3）当滑轮组的机械效率为80％时，物体重多少N?

（1）G

=100N

（2）F=500N（3）G

=800N

4、体重为510N的人，站在水平地面上对地面的压力为N1,.如图20所示，用滑轮组拉物体A沿水平方向做匀速运动，此时人对地面的压力为N2,压力变化了110N。

滑轮组的机械效率为80%。

（不计绳重和摩擦，地面上的定滑轮与物体A相连的绳子沿水平方向，地面上的定滑轮与动滑轮相连的绳子沿竖直方向，人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上，）。

（1）绳对人的拉力；

（2）物体A与地面的摩擦力；

（3）若在物体A上再放一个物体B,滑动摩擦力增大了30N,此时该装置的机械效率是多少？

（7分）

（1）F=110

（2）f＝176

…（3）'

＝82.4%

5．如图25所示，是一个上肢力量健身器示意图。

配重A受到的重力为350N。

B、C都是定滑轮，D是动滑轮；

杠杆EH可绕O点在竖直平面内转动，OE=3OH。

小明受到的重力为500N，当他通过细绳在H点分别施加竖直向下的拉力T1、T2时，杠杆两次都在水平位置平衡，小明对地面的压力分别为F1、F2，配重A受到的拉力分别为FA1、FA2，配重A对地面的压力分别为N1、N2，且两次A对地面的压力相差100N。

已知F1∶F2＝4∶3，N1∶N2＝3∶2。

杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计。

（1）拉力FA2与FA1之差；

（2）小明对地面的压力F1；

（3）当小明通过细绳在H点施加竖直向下的拉力T3时，

配重A匀速上升2cm,此时滑轮组的机械效率η。

（请画出相关受力分析图）

（1）FA2-FA1=100N；

（2）F1=400N；

（3）η=87.5%。

6．图26是一个上肢力量健身器示意图。

配重A受到的重力为1600N，配重A上方连有一根弹簧测力计D，可以显示所受的拉力大小，但当它所受拉力在0～2500N范围内时，其形变可以忽略不计。

B是动滑轮，C是定滑轮；

杠杆EH可绕O点在竖直平面内转动，OE:

OH=1:

6.小阳受到的重力为700N，他通过细绳在H点施加竖直向下的拉力为T1时，杠杆在水平位置平衡，小阳对地面的压力为F1,配重A受到绳子的拉力为

配重A上方的弹簧测力计D显示受到的拉力

为2.1×

103N；

小阳通过细绳在H点施加竖直向下的拉力为T2时，杠杆仍在水平位置平衡，小阳对地面的压力为F2,配重A受到绳子的拉力为

为2.4×

103N.已知

（杠杆EH、弹簧D和细绳的质量均忽略不计,不计绳和轴之间摩擦）。

（1）配重A受到绳子的拉力为

;

（2动滑轮B受到的重力GB；

（3）拉力为T2.

38.

（1）以物体A为研究对象，受力分析如图2甲、乙所示，

物体A始终处于静止状态，所以有

（以上两个式子共1分）

已知GA=1600N，

为2100N，

为2400N，所以可以求得

（1分）

（2）以人为研究对象，受力分析如图3甲、乙所示，

人始终处于静止状态，所以有

因为

大小相等，

大小相等。

所以有

已知

，

得：

①（1分）

对杠杆进行受力分析,如图4甲、乙所示，根据杠杆平衡条件：

图4甲

②

③

（②和③共1分）

已知OE:

6.

图4乙

（FA1和FA2全解正确共1分）

解上面三式可得：

GB=100N（1分）

（3）将GB=100N代入③式，得T2=250N.（1分）