材料力学五章Word文档格式.docx

材料力学五章Word文档格式.docx

《材料力学五章Word文档格式.docx》由会员分享，可在线阅读，更多相关《材料力学五章Word文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

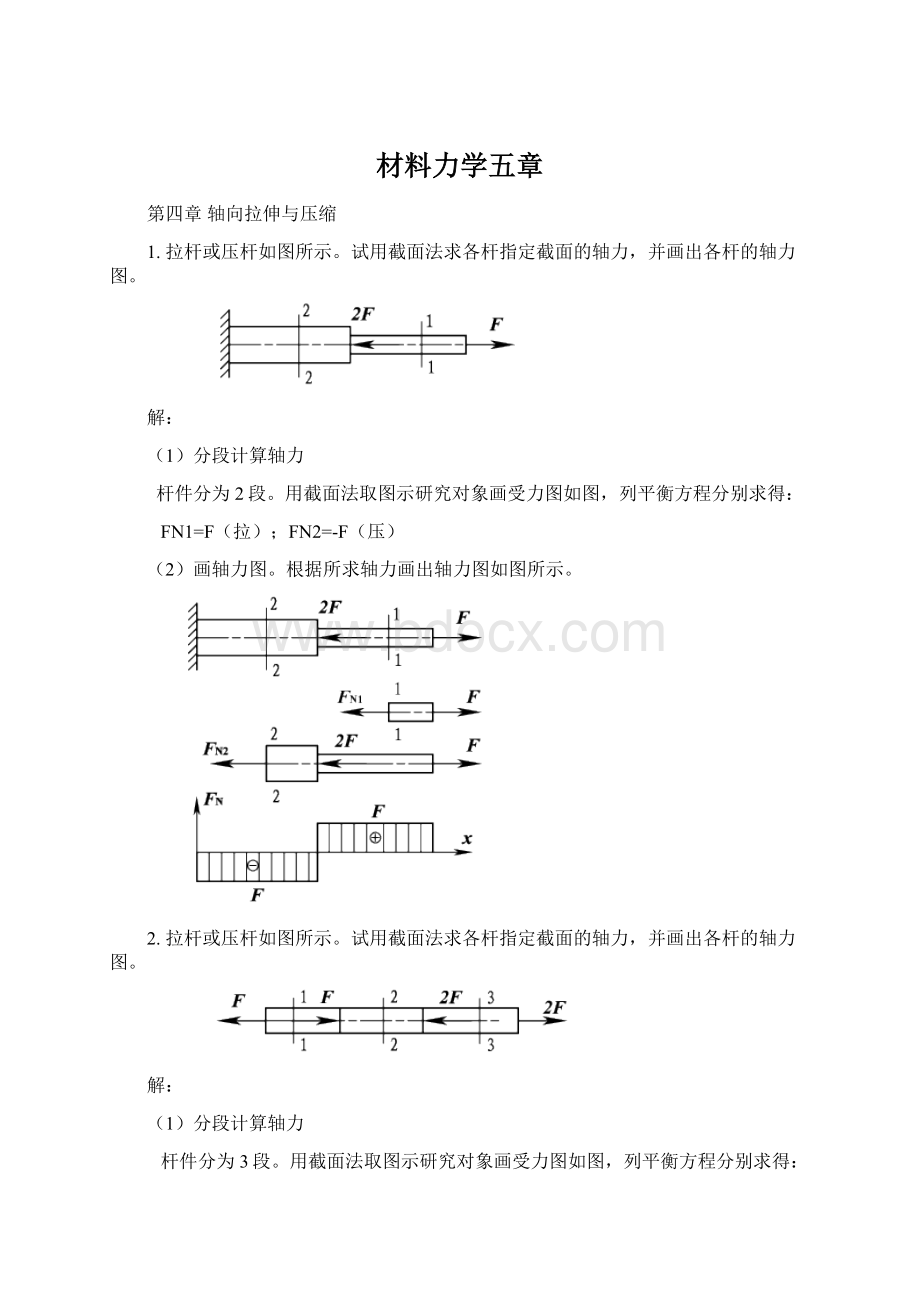
（1）分段计算轴力

杆件分为2段。

用截面法取图示研究对象画受力图如图，列平衡方程分别求得：

FN1=F（拉）；

FN2=-F（压）

（2）画轴力图。

根据所求轴力画出轴力图如图所示。

2.拉杆或压杆如图所示。

杆件分为3段。

FN2=0；

FN3=2F（拉）

3.拉杆或压杆如图所示。

（1）计算A端支座反力。

由整体受力图建立平衡方程：

∑Fx＝0， 

2kN-4kN+6kN-FA＝0

FA＝4kN（←）

（2）分段计算轴力

FN1=-2kN（压）；

FN2=2kN（拉）；

FN3=-4kN（压）

（3）画轴力图。

4.拉杆或压杆如图所示。

FN1=-5kN（压）；

FN2=10kN（拉）；

FN3=-10kN（压）

5.圆截面钢杆长l=3m，直径d=25mm，两端受到F=100kN的轴向拉力作用时伸长Δl=2.5mm。

试计算钢杆横截面上的正应力σ和纵向线应变ε。

6.阶梯状直杆受力如图所示。

已知AD段横截面面积AAD=1000mm2，DB段横截面面积ADB=500mm2，材料的弹性模量E=200GPa。

求该杆的总变形量ΔlAB。

解:

由截面法可以计算出AC，CB段轴力FNAC=-50kN（压），FNCB=30kN（拉）。

7.圆截面阶梯状杆件如图所示，受到F=150kN的轴向拉力作用。

已知中间部分的直径d1=30mm，两端部分直径为d2=50mm，整个杆件长度l=250mm，中间部分杆件长度l1=150mm，E=200GPa。

试求：

1）各部分横截面上的正应力σ；

2）整个杆件的总伸长量。

8.用一根灰口铸铁圆管作受压杆。

已知材料的许用应力为[σ]=200MPa，轴向压力F=1000kN，管的外径D=130mm，内径d=30mm。

试校核其强度。

9.用绳索吊起重物如图所示。

已知F=20kN，绳索横截面面积A=12.6cm2，许用应力[σ]=10MPa。

试校核α=45°

及α=60°

两种情况下绳索的强度。

10.某悬臂吊车如图所示。

最大起重荷载G=20kN，杆BC为Q235A圆钢，许用应力[σ]=120MPa。

试按图示位置设计BC杆的直径d。

11.如图所示AC和BC两杆铰接于C，并吊重物G。

已知杆BC许用应力[σ1]=160MPa，杆AC许用应力[σ2]=100MPa，两杆横截面面积均为A=2cm2。

求所吊重物的最大重量。

12.三角架结构如图所示。

已知杆AB为钢杆，其横截面面积A1=600mm2，许用应力[σ1]=140MPa；

杆BC为木杆，横截面积A2=3×

104mm2，许用应力[σ2]=3.5MPa。

试求许用荷载[F]。

13.图示一板状试样，表面贴上纵向和横向电阻应变片来测定试样的应变。

已知b=4mm，h=30mm，每增加ΔF=3kN的拉力，测得试样的纵向应变ε=120×

10-6，横向应变ε/=-38×

10-6。

试求材料的弹性模量E和泊松比ν。

14.图示正方形截面阶梯状杆件的上段是铝制杆，边长a1=20mm，材料的许用应力[σ1]=80MPa；

下段为钢制杆，边长a2=10mm，材料的许用应力[σ2]=140MPa。

15.两端固定的等截面直杆受力如图示，求两端的支座反力。