最新中考数学二次函数复习题附答案Word文件下载.docx
《最新中考数学二次函数复习题附答案Word文件下载.docx》由会员分享,可在线阅读,更多相关《最新中考数学二次函数复习题附答案Word文件下载.docx(32页珍藏版)》请在冰豆网上搜索。
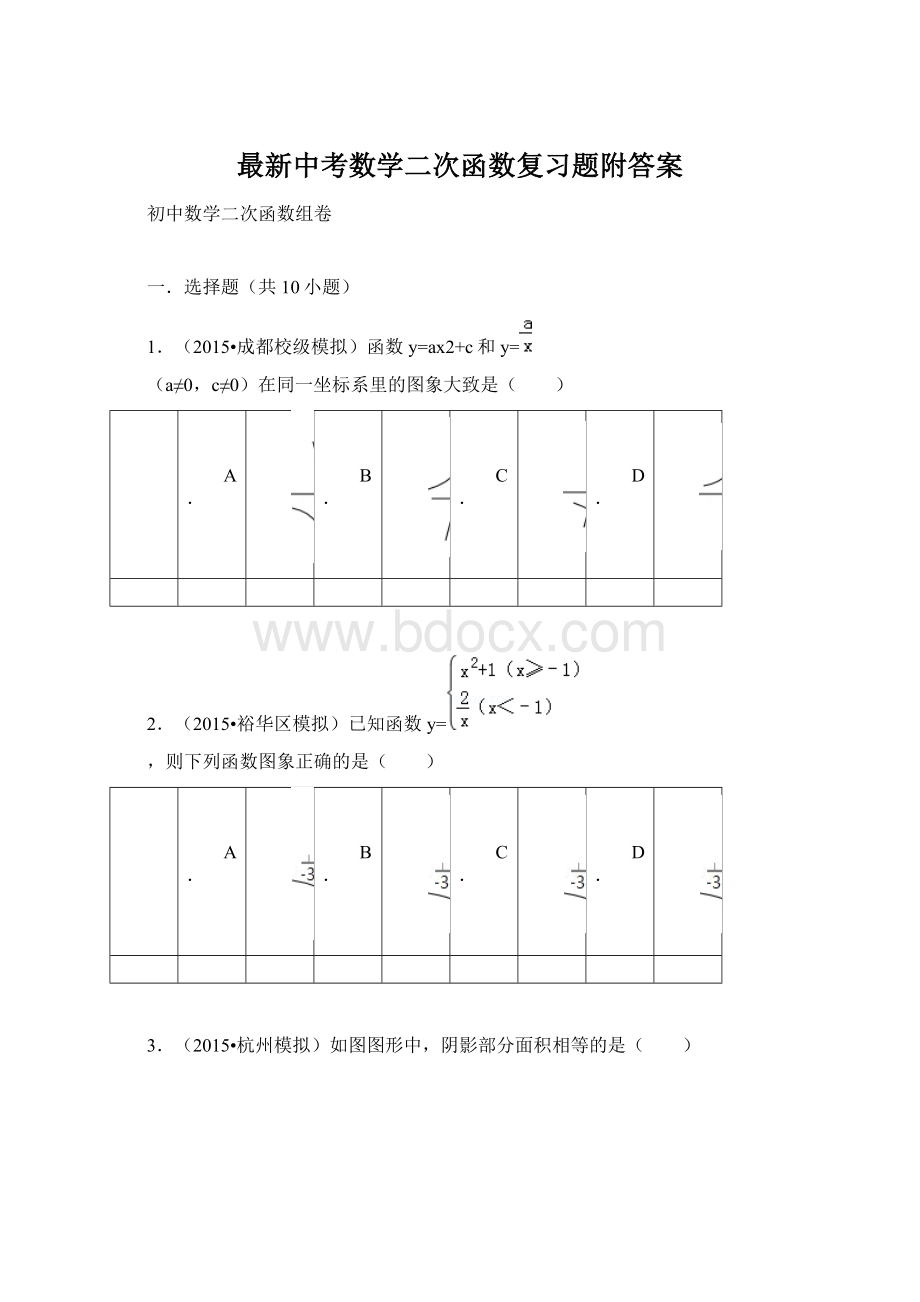
对称轴是y轴
在对称轴的左侧,y随x的增大而增大
最高点是原点
8.(2015•徐汇区一模)已知二次函数y=ax2﹣2x+2(a>0),那么它的图象一定不经过( )
第一象限
第二象限
第三象限
第四象限
9.(2015•莒县一模)如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①abc>0;
②ax2+bx+c=0的两根分别为﹣3和1;
③b>2a;
④﹣2b+c<0;
其中正确的命题是( )
①②
②④
①③
③④
10.(2015•崇明县一模)如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
a>0
b>0
c<0
b2﹣4ac>0
二.填空题(共15小题)
11.(2015•青浦区一模)如果抛物线y=(a+3)x2﹣5不经过第一象限,那么a的取值范围是 .
12.(2015•盐城校级模拟)若抛物线y=x2﹣kx+k﹣1的顶点在x轴上,则k= .
13.(2015•徐汇区一模)二次函数y=x2﹣4x﹣5的图象的对称轴是直线 .
14.(2015•温州模拟)已知二次函数
,若y随x的增大而减小,则x的取值范围是 .
15.(2015•河西区一模)抛物线y=﹣2x2+x﹣4的对称轴为 .
16.(2015•高新区一模)函数y=﹣(x+1)2+5的最大值为 .
17.(2015•大庆校级模拟)用配方法把二次函数y=2x2+3x+1写成y=a(x+m)2+k的形式 .
18.(2015春•张掖校级月考)二次函数y=3(x﹣1)2+2图象的顶点坐标为 .
19.(2014•路桥区模拟)如图,如果反比例函数的图象经过抛物线y=﹣x2﹣2x的顶点,那么这个反比例函数的解析式为 .
20.(2014•杨浦区一模)函数y=(x+5)(2﹣x)图象的开口方向是 .
21.(2015春•锦州校级月考)二次函数y=x2﹣6x+3k的图象与x轴有两个交点,则k的取值范围是 .
22.(2013•本溪)在平面直角坐标系中,把抛物线y=﹣
x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是 .
23.(2012•上海)将抛物线y=x2+x向下平移2个单位,所得抛物线的表达式是 .
24.(2011•黑龙江)抛物线y=﹣
(x+1)2﹣1的顶点坐标为 .
25.(2010•黔东南州)二次函数y=(x+1)2﹣1,当1<y<2时,x的取值范围是 .
三.解答题(共5小题)
26.(2015•福建模拟)求二次函数y=﹣2(x﹣3)2﹣5的顶点坐标.
27.(2015•齐齐哈尔模拟)如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(﹣2,0).
(1)求此二次函数解析式及顶点B的坐标;
(2)在抛物线上有一点P,满足S△AOP=3,直接写出点P的坐标.
28.(2015•嘉定区一模)已知二次函数y=mx2﹣2x+n(m≠0)的图象经过点(2,﹣1)和(﹣1,2),求这个二次函数的解析式,并求出它的图象的顶点坐标和对称轴.
29.(2015•宝山区一模)已知一个二次函数的图象经过点A(1,0)和点B(0,6),C(4,6),求这个抛物线的表达式以及该抛物线的顶点坐标.
30.(2015•岳池县模拟)已知抛物线的顶点坐标是(8,9),且过点(0,1),求该抛物线的解析式.
参考答案与试题解析
考点:
二次函数的图象;
反比例函数的图象.菁优网版权所有
分析:
本题可先由二次函数图象得到字母系数的正负,再与反比例函数的图象相比较看是否一致.逐一排除.
解答:
解:
由A,D中的二次函数图象可得a>0,c=0,因为y=
(a≠0,c≠0),故A,D错误;
由B,C中的二次函数图象可得a<0,c>0,所以y=
(a≠0,c≠0)的图象在二,四象限内,故C错误,B正确.
故选:
点评:
此题主要考查了反比例函数图象与二次函数图象,应该识记反比例函数在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:
开口方向、对称轴等.
分析y=x2+1在x≥﹣1时的性质和y=
在x<﹣1时的性质,选出正确选项即可.
y=x2+1,开口向上,对称轴是y轴,顶点坐标是(0,1),当x≥﹣1时,B、C、D正确;
y=
,图象在第一、三象限,当x<﹣1时,C正确.
本题考查的是二次函数图象和反比例函数图象,正确理解图象与系数之间的关系是解题的关键.
一次函数的图象;
专题:
数形结合.
甲、丙:
根据函数解析式求出图象与x轴,y轴的交点坐标,再计算阴影部分的面积;
乙:
可判断出阴影部分为斜边为4的等腰直角三角形,据此计算阴影部分的面积;
丁:
利用反比例函数系数k的几何意义求出阴影部分的面积.
甲:
直线y=﹣
x+4与x轴交点为(3,0),与y轴的交点为(0,4),则阴影部分的面积为
×
3×
4=6;
阴影部分为斜边为4的等腰直角三角形,其面积为
4×
2=4;
丙:
抛物线y=
﹣2与x轴的两个交点为(﹣3,0)与(3,0),顶点坐标为(0,﹣2),则阴影部分的面积为
6×
2=6;
此函数是反比例函数,那么阴影部分的面积为
6=3;
因此甲、丙的面积相等,
故选B.
此题主要考查了函数图象与坐标轴交点坐标的求法以及图形面积的求法,是基础题,熟练掌握各类函数的图象特点是解决问题的关键.
一次函数的图象.菁优网版权所有
随科技的迅速发展,人们的生活日益趋向便捷、快速,方便,对于我国传统的手工艺制作,也很少有人问津,因此,我组想借此创业机会,在校园内开个DIY创意小屋。
它包括编织、刺绣、串珠等,让我们传统的手工制作也能走进大学,丰富我们的生活。
为此,装潢美观,亮丽,富有个性化的店面环境,能引起消费者的注意,从而刺激顾客的消费欲望。
这些问题在今后经营中我们将慎重考虑的。
可先根据一次函数的图象判断k的符号,再判断二次函数图象与实际是否相符,判断正误.
年轻有活力是我们最大的本钱。
我们这个自己动手做的小店,就应该与时尚打交道,要有独特的新颖性,这正是我们年轻女孩的优势。
1、DIY手工艺市场状况分析解:
A、由一次函数y=kx+k的图象可得:
k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
beadorks公司成功地创造了这样一种气氛:
商店和顾客不再是单纯的买卖关系,营业员只是起着参谋的作用,顾客成为商品或者说是作品的作参与者,营业员和顾客互相交流切磋,成为一个共同的创作体B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
新材料手工艺品。
目前,国际上传统的金银、仿金银制成饰品的销售在逐步下降,与此形成鲜明对比的是,数年以前兴起的崇尚然风格、追求个性的自制饰品--即根据自己的创意将各种材质的饰珠,用皮、布、金属等线材串出的品,正在各国的女性中大行其道。
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.
本题考查的是一次函数和二次函数的图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:
开口方向、对称轴、顶点坐标.
1、作者:
蒋志华《市场调查与预测》,中国统计出版社2002年8月§
11-2市场调查分析书面报告
我们长期呆在校园里,没有工作收入一直都是靠父母生活,在资金方面会表现的比较棘手。
不过,对我们的小店来说还好,因为我们不需要太多的投资。
(二)DIY手工艺品的“热卖化”C.
(4)信息技术优势D.
二次函数的性质.菁优网版权所有
根据顶点式的意义直接解答即可.
二次函数y=(x﹣2)2+1的图象的顶点坐标是(2,1).
故选A.
本题考查了二次函数的性质,要熟悉顶点式的意义,并明确:
y=a(x﹣h)2+k(a≠0)的顶点坐标为(h,k).
由抛物线解析式可知,二次项系数a=1>0,可知抛物线开口向上.
∵二次函数y=x2的二次项系数a=1>0,
∴抛物线开口向上.
本题考查了抛物线的开口方向与二次项系数符号的关系.当a>0时,抛物线开口向上,当a<0时,抛物线开口向下.
此题应从二次函数的基本形式入手,它符合y=ax2的基本形式,根据它的性质,进行解答.
因为a<0,所以开口向下,顶点坐标(0,0),对称轴是y轴,有最高点是原点.
A
此题主要考查y=ax2形式二次函数的基本性质,比较基础,但也是中考中热点问题.
先根据题意判断出二次函数的对称轴方程,再令x=0求出y的值,进而可得出结论.
∵二次函数y=ax2﹣2x+2(a>0)的对称轴为直线x=﹣
=﹣
=
>0,
∴其顶点坐标在第一或四象限,
∵当x=0时,y=2,
∴抛物线一定经过第二象限,
∴此函数的图象一定不经过第三象限.
故选C.
本题考查的是二次函数的性质,熟知二次函数的对称轴方程是解答此题的关键.
二次函数图象与系数的关系.菁优网版权所有
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
①抛物线开口向上,a>0,
抛物线与y轴交于负半轴,c<0,
对称轴在y轴的左侧,b>0,
∴abc<0,①错误;
②由抛物线的对称性可知,
ax2+bx+c=0的两根分别为﹣3和1,②正确;
③对称轴﹣
=﹣1,b=2a,③错误;
④x=﹣2时,y<0,
4a﹣2b+c<0,
﹣2b+c<﹣4a,4a>0,
∴﹣2b+c<0,④正确,
本题考查的是二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定,二次函数y=ax2+bx+c与x轴交点的横坐标即为方程ax2+bx+c=0的两个根.
首先根据开口方向确定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0.
由图象的开口向上可得a开口向上,由x=﹣
>0,可得b<0,
由二次函数y=ax2+bx+c的图象交y轴于负半轴可得c<0,
由二次函数y=ax2+bx+c的图象与x轴有两个交点,可得b2﹣4ac>0,所以B不正确.
本题主要考查二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,此题运用了数形结合思想.
11.(2015•青浦区一模)如果抛物线y=(a+3)x2﹣5不经过第一象限,那么a的取值范围是 a<﹣3 .
根据抛物线y=(a+3)x2﹣5不经过第一象限可以确定不等式的开口方向,从而确定a的取值范围.
∵抛物线y=(a+3)x2﹣5不经过第一象限,
∴a+3<0,
解得:
a<﹣3,
故答案为:
a<﹣3.
考查了二次函数的性质,根据抛物线的开口方向,与y轴的交点,对称轴判断抛物线经过的象限.
12.(2015•盐城校级模拟)若抛物线y=x2﹣kx+k﹣1的顶点在x轴上,则k= 2 .
顶点在x轴上,所以顶点的纵坐标是0.
根据题意得
=0,
解得k=2.
2.
本题考查求抛物线顶点纵坐标的公式,比较简单,牢记公式是解题的关键.
13.(2015•徐汇区一模)二次函数y=x2﹣4x﹣5的图象的对称轴是直线 x=2 .
根据二次函数的对称轴公式列式计算即可得解.
对称轴为直线x=﹣
=2,
即直线x=2.
x=2.
本题考查了二次函数的性质,主要利用了对称轴公式,需熟记.
,若y随x的增大而减小,则x的取值范围是 x≤1 .
根据二次函数的解析式的二次项系数判定该函数图象的开口方向、根据顶点式方程确定其图象的顶点坐标,从而知该二次函数的单调区间.
∵二次函数的解析式
的二次项系数是
,
∴该二次函数的开口方向是向上;
又∵该二次函数的图象的顶点坐标是(1,4),
∴该二次函数图象在[﹣∞1m]上是减函数,即y随x的增大而减小;
即:
当x≤1时,y随x的增大而减小,
x≤1.
本题考查了二次函数图象的性质.解答该题时,须熟知二次函数的系数与图象的关系、二次函数的顶点式方程y=(k﹣h)x2﹣b中的h,b的意义.
15.(2015•河西区一模)抛物线y=﹣2x2+x﹣4的对称轴为
.
根据抛物线y=ax2+bx+c的对称轴公式为X=﹣
,此题中的a=﹣4,b=3,将它们代入其中即可.
x=﹣
.
故答案为
本题考查二次函数对称轴公式的应用,熟练掌握对称轴公式是解题的关键.
16.(2015•高新区一模)函数y=﹣(x+1)2+5的最大值为 5 .
二次函数的最值.菁优网版权所有
根据二次函数的性质a=﹣1<0,函数有最大值5.
∵﹣1<0,
∴函数y=﹣(x+1)2+5的最大值为5.
5.
本题考查的是二次函数的性质,二次函数y=a(x﹣h)2+k,当a>0时,函数有最小值k,当a<0时,函数有最大值k.
17.(2015•大庆校级模拟)用配方法把二次函数y=2x2+3x+1写成y=a(x+m)2+k的形式 y=2(x+
)2﹣
二次函数的三种形式.菁优网版权所有
把二次函数y=2x2+3x+1用配方法化为顶点式即可.
y=2x2+3x+1
=2(x+
y=2(x+
本题考查的是用配方法把一般式化为顶点式,掌握配方法是解题的关键,y=ax2+bx+c=a(x+
)2+
18.(2015春•张掖校级月考)二次函数y=3(x﹣1)2+2图象的顶点坐标为 (1,2) .
二次函数的性质;
函数思想.
二次函数y=a(x﹣h)2+k(a≠0)的顶点坐标是(h,k).
根据二次函数的顶点式方程y=3(x﹣1)2+2知,该函数的顶点坐标是:
(1,2).
故答案是:
本题考查了二次函数的性质和二次函数的三种形式.解答该题时,需熟悉二次函数的顶点式方程y=a(x﹣h)2+k中的h、k所表示的意义.
19.(2014•路桥区模拟)如图,如果反比例函数的图象经过抛物线y=﹣x2﹣2x的顶点,那么这个反比例函数的解析式为 y=
待定系数法求反比例函数解析式.菁优网版权所有
利用二次函数的性质求出抛物线的顶点坐标,代入反比例函数的解析式为y=
求解即可.
∵抛物线y=﹣x2﹣2x=﹣(x+1)2+1,
∴抛物线的顶点为(﹣1,1),
设反比例函数的解析式为y=
把(﹣1,1),代入得k=﹣1,
∴反比例函数的解析式为y=
本题主要考查了二次函数的性质及待定系数法求反比例函数解析式,解题的关键是求出抛物线的顶点坐标.
20.(2014•杨浦区一模)函数y=(x+5)(2﹣x)图象的开口方向是 向下 .
首先将二次函数化为一般形式,然后根据二次项系数的符号确定开口方向.
y=(x+5)(2﹣x)=﹣x2+3x+10,
∵a=﹣1<0,
∴开口向下,
向下.
本题考查了二次函数的性质,解题的关键是正确的化为一般形式.
21.(2015春•锦州校级月考)二次函数y=x2﹣6x+3k的图象与x轴有两个交点,则k的取值范围是 k<3 .
抛物线与x轴的交点.菁优网版权所有
根据判别式b2﹣4ac与零的关系即可判断出二次函数y=x2﹣6x+3k的图象与x轴交点的个数.
根据题意,得△=b2﹣4ac>0,
即(﹣6)2﹣4×
1×
3k>0,
k<3.
本题考查了二次函数y=ax2+bx+c的图象与x轴交点的个数的判断,理解△=b2﹣4ac>0时,二次函数的图象与x轴有两个交点是解题关键.
x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是 y=﹣
(x+1)2+4 .
二次函数图象与几何变换.菁优网版权所有
先求出原抛物线的顶点坐标,再根据向左平移横坐标减,向上平移纵坐标加求出平移后的抛物线的顶点坐标,然后写出抛物线解析式即可.
∵抛物线y=﹣
x2+1的顶点坐标为(0,1),
∴向上平移3个单位,再向左平移1个单位后的抛物线的顶点坐标为(﹣1,4),
∴所得抛物线的解析式为y=﹣
(x+1)2+