51单片机PID算法程序三增量式PID控制算法Word文档下载推荐.docx
《51单片机PID算法程序三增量式PID控制算法Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《51单片机PID算法程序三增量式PID控制算法Word文档下载推荐.docx(18页珍藏版)》请在冰豆网上搜索。
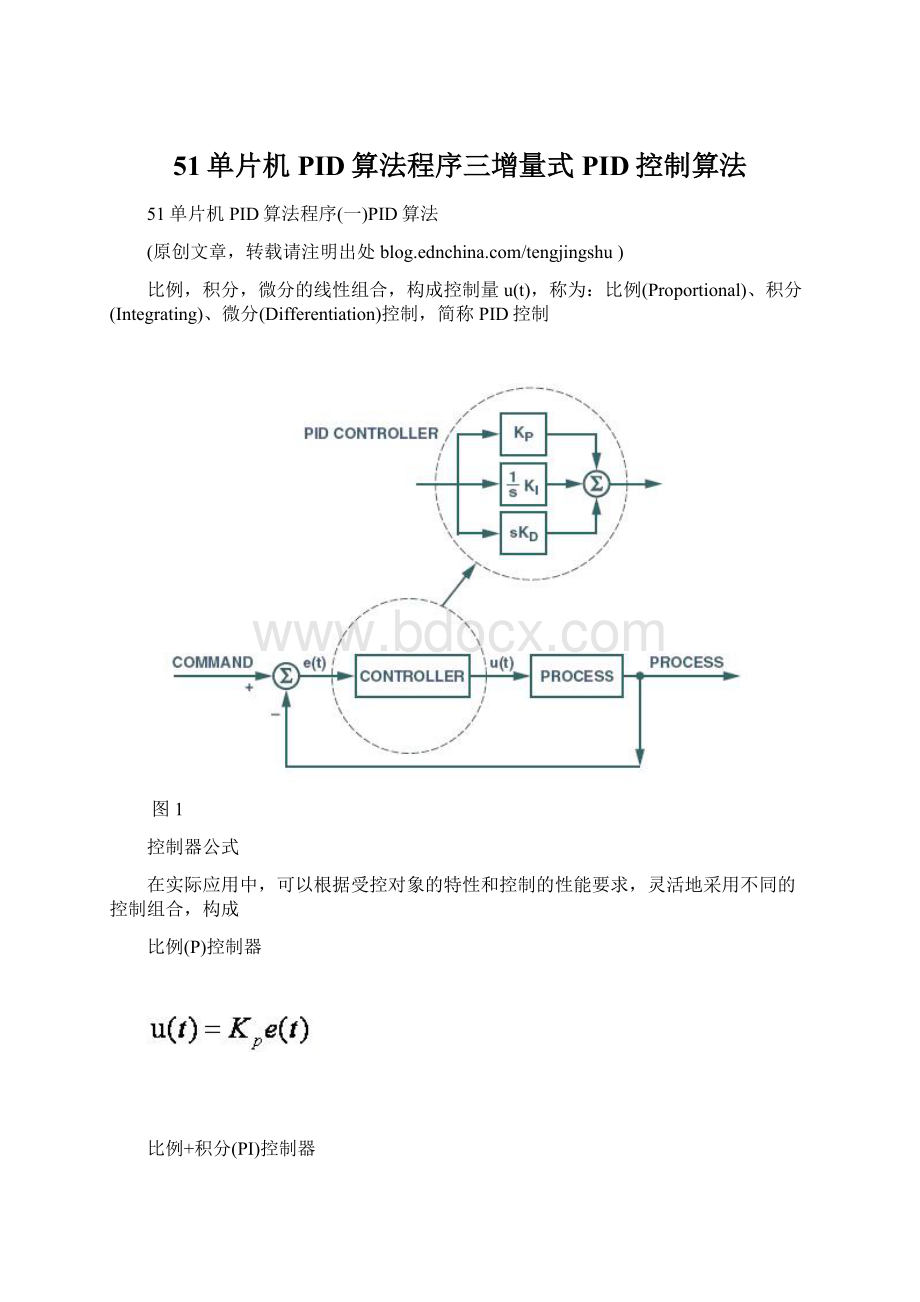
积分(I)控制
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
为了减小稳态误差,在控制器中加入积分项,积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即使误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减少,直到等于零。
积分(I)和比例(P)通常一起使用,称为比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
如果单独用积分(I)的话,由于积分输出随时间积累而逐渐增大,故调节动作缓慢,这样会造成调节不及时,使系统稳定裕度下降。
图3积分(I)控制和比例积分(PI)控制阶跃相应
微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
由于自动控制系统有较大的惯性组件(环节)或有滞后(delay)组件,在调节过程中可能出现过冲甚至振荡。
解决办法是引入微分(D)控制,即在误差很大的时候,抑制误差的作用也很大;
在误差接近零时,抑制误差的作用也应该是零。
图4微分(D)控制和比例微分(PD)控制阶跃相应
总结:
PI比P少了稳态误差,PID比PI反应速度更快并且没有了过冲。
PID比PI有更快的响应和没有了过冲。
图5
增益常数(系数)
上升时间
过冲
建立时间
稳态误差
Kp
减少
增大
很小变化
减小
KI
增加
消除
KD
表1
注意,这里的
图6典型的PID控制器对于阶跃跳变参考输入的响应
参数的调整
应用PID控制,必须适当地调整比例放大系数KP,积分时间TI和微分时间TD,使整个控制系统得到良好的性能。
最好的寻找PID参数的办法是从系统的数学模型出发,从想要的反应来计算参数。
很多时候一个详细的数学描述是不存在的,这时候就需要实际地调节PID的参数.
Ziegler-Nichols方法
Ziegler-Nichols方法是基于系统稳定性分析的PID整定方法.在设计过程中无需考虑任何特性要求,整定方法非常简单,但控制效果却比较理想。
具体整定方法步骤如下:
1.先置I和D的增益为0,逐渐增加KP直到在输出得到一个持续的稳定的振荡。
2.记录下振荡时的P部分的临界增益Kc,和振荡周期Pc,代到下表中计算出KP,Ti,Td。
Ziegler-Nichols整定表
表2
Tyreus-Luyben整定表:
表3
Tyreus-Luyben的整定值减少了振荡的作用和增强了稳定性。
自动测试方法:
为了确定过程的临界周期Pc和临界增益Kc,控制器会临时使它的PID
算法失效,取而代之的是一个ON/OFF的继电器来让过程变为振荡的。
这
两个参数很好的将过程行为进行了量化以决定PID控制器应该如何整定来
得到理想的闭环回路性能。
图6
参考资料
1)Mixed-SignalControlCircuitsUseMicrocontrollerforFlexibilityinImplementingPIDAlgorithms,ByEamonNeary
(图1,表1)
2)Atmel8-bitAVRMicrocontrollersApplicationNote:
AVR221:
DiscretePIDcontroller
(图2,图3,图4,图5,表2)
3)使用Ziegler-Nichols方法的自整定控制
(图6)
4)Ziegler-NicholsMethod
http:
//www.chem.mtu.edu/~tbco/cm416/zn.html
(表3)
5)Ziegler-Nichols方法PID参数整定--随风的blog
6)PID控制原理教程,胡晓若编制
51单片机PID算法程序
(二)位置式PID控制算法
(转载请注明出处)
由51单片机组成的数字控制系统控制中,PID控制器是通过PID控制算法实现的。
51单片机通过AD对信号进行采集,变成数字信号,再在单片机中通过算法实现PID运算,再通过DA把控制量反馈回控制源。
从而实现对系统的伺服控制。
位置式PID控制算法
位置式PID控制算法的简化示意图
上图的传递函数为:
(2-1)
在时域的传递函数表达式
(2-2)
对上式中的微分和积分进行近似
(2-3)
式中n是离散点的个数。
于是传递函数可以简化为:
(2-4)
其中
u(n)——第k个采样时刻的控制;
KP——比例放大系数;
Ki——积分放大系数;
Kd——微分放大系数;
T——采样周期。
如果采样周期足够小,则(2-4)的近似计算可以获得足够精确的结果,离散控制过程与连续过程十分接近。
(2-4)表示的控制算法直接按(2-1)所给出的PID控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式PID控制算法。
缺点:
1)
由于全量输出,所以每次输出均与过去状态有关,计算时要对e(k)(k=0,1,…n)进行累加,工作量大。
2)
因为计算机输出的u(n)对应的是执行机构的实际位置,如果计算机出现故障,输出u(n)将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实际生产中是不允许的。
位置式PID控制算法C51程序
具体的PID参数必须由具体对象通过实验确定。
由于单片机的处理速度和ram资源的限制,一般不采用浮点数运算,而将所有参数全部用整数,运算
到最后再除以一个2的N次方数据(相当于移位),作类似定点数运算,可大大提高运算速度,根据控制精度的不同要求,当精度要求很高时,注意保留移位引起的“余数”,做好余数补偿。
这个程序只是一般常用pid算法的基本架构,没有包含输入输出处理部分。
=====================================================================================================*/
#include<
reg52.h>
string.h>
//C语言中memset函数头文件
/*====================================================================================================
PIDFunction
ThePID(比例、积分、微分)functionisusedinmainly
controlapplications.PIDCalcperformsoneiterationofthePID
algorithm.
WhilethePIDfunctionworks,mainisjustadummyprogramshowing
atypicalusage.
typedefstructPID{
doubleSetPoint;
//设定目标Desiredvalue
doubleProportion;
//比例常数ProportionalConst
doubleIntegral;
//积分常数IntegralConst
doubleDerivative;
//微分常数DerivativeConst
doubleLastError;
//Error[-1]
doublePrevError;
//Error[-2]
doubleSumError;
//SumsofErrors
}PID;
PID计算部分
doublePIDCalc(PID*pp,doubleNextPoint)
{
doubledError,Error;
Error=pp->
SetPoint-NextPoint;
//偏差
pp->
SumError+=Error;
//积分
dError=Error-pp->
LastError;
//当前微分
PrevError=pp->
LastError=Error;
return(pp->
Proportion*Error//比例项
+pp->
Integral*pp->
SumError//积分项
Derivative*dError//微分项
);
}
InitializePIDStructurePID参数初始化
voidPIDInit(PID*pp)
memset(pp,0,sizeof(PID));
MainProgram主程序
=====================================================================================================*
doublesensor(void)//DummySensorFunction
return100.0;
voidactuator(doublerDelta)//DummyActuatorFunction
{}
voidmain(void)
PIDsPID;
//PIDControlStructure
doublerOut;
//PIDResponse(Output)
doublerIn;
//PIDFeedback(Input)
PIDInit(&
sPID);
//InitializeStructure
sPID.Proportion=0.5;
//SetPIDCoefficients
sPID.Integral=0.5;
sPID.Derivative=0.0;
sPID.SetPoint=100.0;
//SetPIDSetpoint
for(;
;
){//MockUpofPIDProcessing
rIn=sensor();
//ReadInput
rOut=PIDCalc(&
sPID,rIn);
//PerformPIDInteration
actuator(rOut);
//EffectNeededChanges
}
参考资料:
1)Atmel8-bitAVRMicrocontrollersApplicationNote:
DiscretePIDcontroller
2)茶壶-pidC程序,好东西-腾讯博客–Qzone
3)
PID调节控制做电机速度控制,SUNPLUS凌阳科技
51单片机PID算法程序(三)增量式PID控制算法
当执行机构需要的不是控制量的绝对值,而是控制量的增量(例如去驱动步进电动机)时,需要用PID的“增量算法”。
增量式PID控制算法可以通过(2-4)式推导出。
由(2-4)可以得到控制器的第k-1个采样时刻的输出值为:
(2-5)
将(2-4)与(2-5)相减并整理,就可以得到增量式PID控制算法公式为:
(2-6)
由(2-6)可以看出,如果计算机控制系统采用恒定的采样周期T,一旦确定A、B、C,只要使用前后三次测量的偏差值,就可以由(2-6)求出控制量。
增量式PID控制算法与位置式PID算法(2-4)相比,计算量小得多,因此在实际中得到广泛的应用。
位置式PID控制算法也可以通过增量式控制算法推出递推计算公式:
(2-7)
(2-7)就是目前在计算机控制中广泛应用的数字递推PID控制算法。
增量式PID控制算法C51程序
=====================================================================================================*/
typedefstructPID
intSetPoint;
//设定目标DesiredValue
longSumError;
//误差累计
//比例常数ProportionalConst
//积分常数IntegralConst
//微分常数DerivativeConst
intLastError;
//Error[-1]
intPrevError;
//Error[-2]
staticPIDsPID;
staticPID*sptr=&
sPID;
voidIncPIDInit(void)
sptr->
SumError=0;
LastError=0;
PrevError=0;
Proportion=0;
Integral=0;
//积分常数IntegralConst
Derivative=0;
SetPoint=0;
增量式PID计算部分
intIncPIDCalc(intNextPoint)
registerintiError,iIncpid;
//当前误差
iError=sptr->
//增量计算
iIncpid=sptr->
Proportion*iError//E[k]项
-sptr->
Integral*sptr->
LastError//E[k-1]项
+sptr->
Derivative*sptr->
PrevError;
//E[k-2]项
//存储误差,用于下次计算
PrevError=sptr->
LastError=iError;
//返回增量值
return(iIncpid);
1)PID调节控制做电机速度控制,SUNPLUS凌阳科技
2)增量式PID控制模块程序设计