统计学练习题计算题Word文档格式.docx
《统计学练习题计算题Word文档格式.docx》由会员分享,可在线阅读,更多相关《统计学练习题计算题Word文档格式.docx(18页珍藏版)》请在冰豆网上搜索。
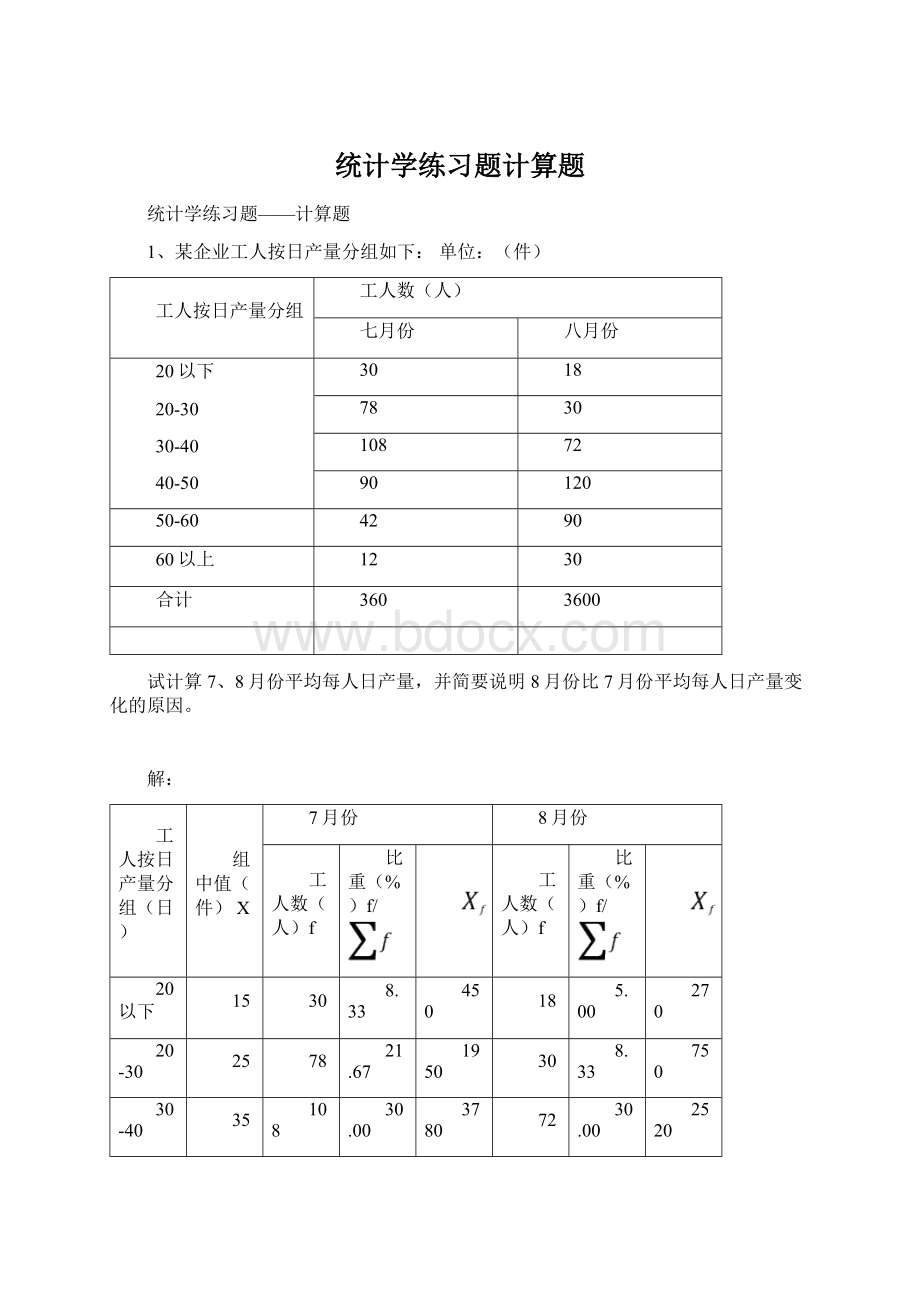
780
—
100.00
13320
15840
7月份平均每人日产量为:
8月份平均每人日产量为:
根据计算结果得知8月份比7月份平均每人日产量多7件。
其原因是不同组日产量水平的工人所占比重发生变化所致。
7月份工人日产量在40件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则为66.67%。
2、某纺织厂生产某种棉布,经测定两年中各级产品的产量资料如下:
产品等级
产量(万米)
2009年
2010年
一级
二级
200
40
24
三级
10
6
250
300
试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。
2009年棉布的平均等级=
=1.24(级)
2010年棉布的平均等级=
=1.12(级)
可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由1.24级上升为1.12级。
质量提高的原因是棉布一级品由80%上升为90%,同时二级品和三级品分别由16%及4%下降为8%及2%。
3、甲乙两企业生产同种产品,1月份各批产量和单位产品成本资料如下:
甲企业
乙企业
单位产品成本
(元)
产量比重
(%)
第一批
第二批
1.0
1.2
1.1
20
第三批
70
试比较和分析哪个企业的单位成本高,为什么?
甲企业的平均单位产品成本=1.0×
10%+1.1×
20%+1.2×
70%=1.16(元)
乙企业的平均单位产品成本=1.2×
30%+1.1×
30%+1.0×
40%=1.09(元)
可见甲企业的单位产品成本较高,其原因是甲企业生产的3批产品中,单位成本较高(1.2元)的产品数量占70%,而乙企业只占30%。
4、有四个地区销售同一种产品,其销售量和销售额资料如下:
地区
销售量(千件)
销售额(万元)
甲
50
乙
176
丙
60
丁
80
384
试计算各地区平均价格和此种商品在四个地区总的平均价格。
总平均价格=
=46.09
5、某商店售货员的工资资料如下:
工资额(元)
售货员人数(人)
375
4
430
3
510
7
590
690
根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准差系数。
工资额(元)X
Xf
1
1500
-135
540
72900
2
1290
-80
240
19200
3570
1770
5
2070
180
97200
2595
10200
1560
208500
⑴
=510(元);
⑵全距=690-375=315(元)
⑶
=78(元);
⑷
=102.1(元)⑸
=15.29%;
⑹
=20.02%
6、某班甲乙两个学习小组某科成绩如下:
甲小组
成绩
人数
60分以下
60-70
70-80
80-90
90分以上
乙小组
9
试比较甲乙两个学习小组该科平均成绩的代表性大小。
成绩(分)
组中值
xf
165
18.75
3513.56
1054.69
325
8.75
76.56
382.81
75
750
1.25
1.56
15.63
85
340
11.25
126.56
506.25
90以上
95
191
21.25
451.56
903.13
——
2936.25
=73.75(分)
=11.06(分)
×
100%=15.00%
55
110
-19.58
383.38
766.75
65
390
-9.58
91.78
550.66
675
0.42
0.18
1.59
425
10.42
108.58
542.88
190
20.42
416.98
833.95
1790
2695.83
=74.58(分)
=10.60(分)
100%=14.21%
计算结果得知乙小组标准差系数小,所以乙小组平均成绩代表性大。
7、某机械厂铸造车间生产600吨铸件,合格540吨,试求平均合格率,标准差及标准差系数。
标准差
100%=30%
标准差系数
8、某地区2005年各月总产值资料如下:
月份
总产值(万元)
4200
5000
4400
8
5200
4600
4820
4850
11
5500
4900
5600
请计算各季平均每月总产值和全年平均每月总产值。
第一季度平均每月总产值=4400万元
第二季度平均每月总产值≈4856.7万元
第三季度平均每月总产值=5200万元
第四季度平均每月总产值=5500万元
全年平均每月总产值=4989.2万元
9、2013年末,某储蓄所按2420户的定期储蓄存款账号,进行不重复抽样得到如下资料:
定期储蓄存款(元)
户数(户)
100以下
58
100-300
150
300-500
500-800
62
800以上
14
484
试以0.9545概率对下列指标作区间估计:
(1)平均每户定期存款;
(2)定期存款在300元及300元以上户的比重。
[提示:
100元以下的组中值为50元,t=2。
平均数保留一位,成数(用系数表示)保留两位小数]
组中值x
2900
5013288
30000
3110400
400
800000
627200
650
40300
5805432
950
13300
5141304
-
166500
19697624
(列表计算2分)
(1)平均定期存款区间估计:
平均每户定期存款为:
抽样平均误差:
抽样极限误差:
平均定期存款区间估计:
即在:
327.6~360.4
(2)存款在300元及300元以上户的比重:
即:
存款在300元及以上户的比重区间为53%~61%之间。
10、某企业2005年各月月初职工人数资料如下:
日期
1月
2月
3月
4月
5月
6月
7月
8月
9月
10月
11月
12月
2006年1月1日
职工人数(人)
304
306
308
314
312
320
342
345
350
请计算该企业2005年各季平均职工人数和全年平均职工人数。
第一季度平均职工人数≈302人
第二季度平均职工人数≈310人
第三季度平均职工人数=322人
第四季度平均职工人数=344人
全年平均职工人数≈320人
11、2000年和第十个五年计划时期某地区工业总产值资料如下:
时期
2000年
2001年
2002年
2003年
2004年
2005年
工业总产值(万元)
343.3
447.0
519.7
548.7
703.6
783.9
请计算各种动态指标,并说明如下关系:
⑴发展速度和增长速度;
⑵定基发展速度和环比发展速度;
⑶逐期增长量与累计增长量;
⑷平均发展速度与环比发展速度;
⑸平均发展速度与平均增长速度。
计算如果如下表:
单位
工业总产值
万元
343.3
447.0
519.7
548.7
703.6
783.9
累计增长量
—
103.7
176.4
205.4
360.3
440.6
逐年增长量
72.7
29.0
154.9
80.3
定基发展速度
%
130.21
151.38
159.83
204.95
228.34
环比发展速度
116.26
105.58
128.23
111.41
定基增长速度
30.21
51.38
59.83
104.95
128.34
环比增长速度
16.26
5.58
28.23
11.41
“十五”时期工业总产值平均发展速度=
=117.96%
各种指标的相互关系如下:
⑴增长速度=发展速度-1,如2001年工业总产值发展速度为130.21%,同期增长速度=130.21%-100%=30.21%
⑵定基发展速度=各年环比发展速度连乘积,如2005年工业总产值发展速度228.34%=130.21%×
116.2%×
105.58%×
128.23%×
111.41%
⑶累计增长量=各年逐期增长量之和,如2005年累计增长量440.6=103.7+72.7+29.0+154.9+80.3
⑷平均发展速度等于环比发展速度的连乘积再用其项数开方。
如“十五”期间工业总产值平均发展速度=
⑸平均增长速度=平均发展速度-1,如“十五”期间平均增长速度17.96%=117.96%-100%
12、某厂职工人数及非生产人员数资料如下:
1月1日
2月1日
3月1日
4月1日
5月1日
6月1日
7月1日
4000
4040
4080
4070
4090
4100
其中:
非生产人员数(人)
724
716
682
694
666
660
要求:
⑴计算第一季度和第二季度非生产人员比重,并进行比较;
⑵计算上半年非生产人员比重。
[1]第一季度非生产人员比重:
17.4%;
第二季度非生产人员比重:
16.4%;
∴第二季度指标值比第一季度少1%。
[2]上半年非生产人员比重:
16.9%。
13、某企业历年若干指标资料如下表:
单位:
年度
发展水平
增减量
平均增减量
发展速度%
增减速度%
累计
逐期
定基
环比
2000
285
2001
42.5
2002
106.2
2003
45.2
2004
136.0
2005
3.2
试根据上述资料,计算表中所缺的数字。
各指标计算见下表:
年份
发展
水平
增减量
平均
增减值
发展速度(%)
增减速度
100.0
327.5
114.9
14.9
391.2
106.2
63.7
53.1
137.3
119.5
37.3
19.5
413.8
128.8
22.6
42.9
145.2
105.8
5.8
562.8
277.8
149.0
69.5
197.5
97.5
36.0
580.8
295.8
18.0
69.2
203.8
103.2
103.8
3.2
14、有三种商品的销量和售价资料如下
商品
销量
售价(元)
q0
q1
p0
p1
甲(件)
乙(台)
1000
800
丙(套)
2500
100
计算分析销量和售价的变动对销售额变动的影响。
(略)
说明:
按如下公式建立指标体系并计算
15、某企业职工人数和工资资料统计如下:
组别
人数(人)
人均月收入(元)
基期f0
报告期f1
基期x0
报告期x1
技术人员
普通职工
50
60
1450
3200
1860
根据资料,从相对数和绝对数两个方面分析工人结构变化及各组平均工资水平的变动对总体平均工资的影响。
解:
16、某灯管厂生产10万只日光灯管,现采用简单随机不重复抽样方式抽取1%灯管进行质量检验,测试结果如下:
耐用时间(小时)
灯管数(只)
800小时以下
800-900
900-1000
1000-1100
1100小时以上
根据上述资料:
(1)试计算抽样总体灯管的平均耐用时间
(2)在99.73%的概率保证程度下,估计10万只灯管平均耐用时间的区间范围/
(3)按质量规定,凡耐用时间不及800小时的灯管为不合格品,试计算抽样总体灯管的合格率,并在95%的概率保证程度下,估计10万只灯管的合格率区间范围。
(4)若上述条件不变,只是抽样极限误差可放宽到40小时,在99.73%的概率保证程度下,作下一次抽样抽查,需抽多少只灯管检验?
列表计算:
灯管数(只)f
x
7500
484000
850
128500
216000
33250
14000
1050
26250
160000
1150
17250
486000
97000
1360000
(1)
(2)
(3)
(4)