华师版数学八年级上册知识点总结.doc

华师版数学八年级上册知识点总结.doc

《华师版数学八年级上册知识点总结.doc》由会员分享，可在线阅读，更多相关《华师版数学八年级上册知识点总结.doc（7页珍藏版）》请在冰豆网上搜索。

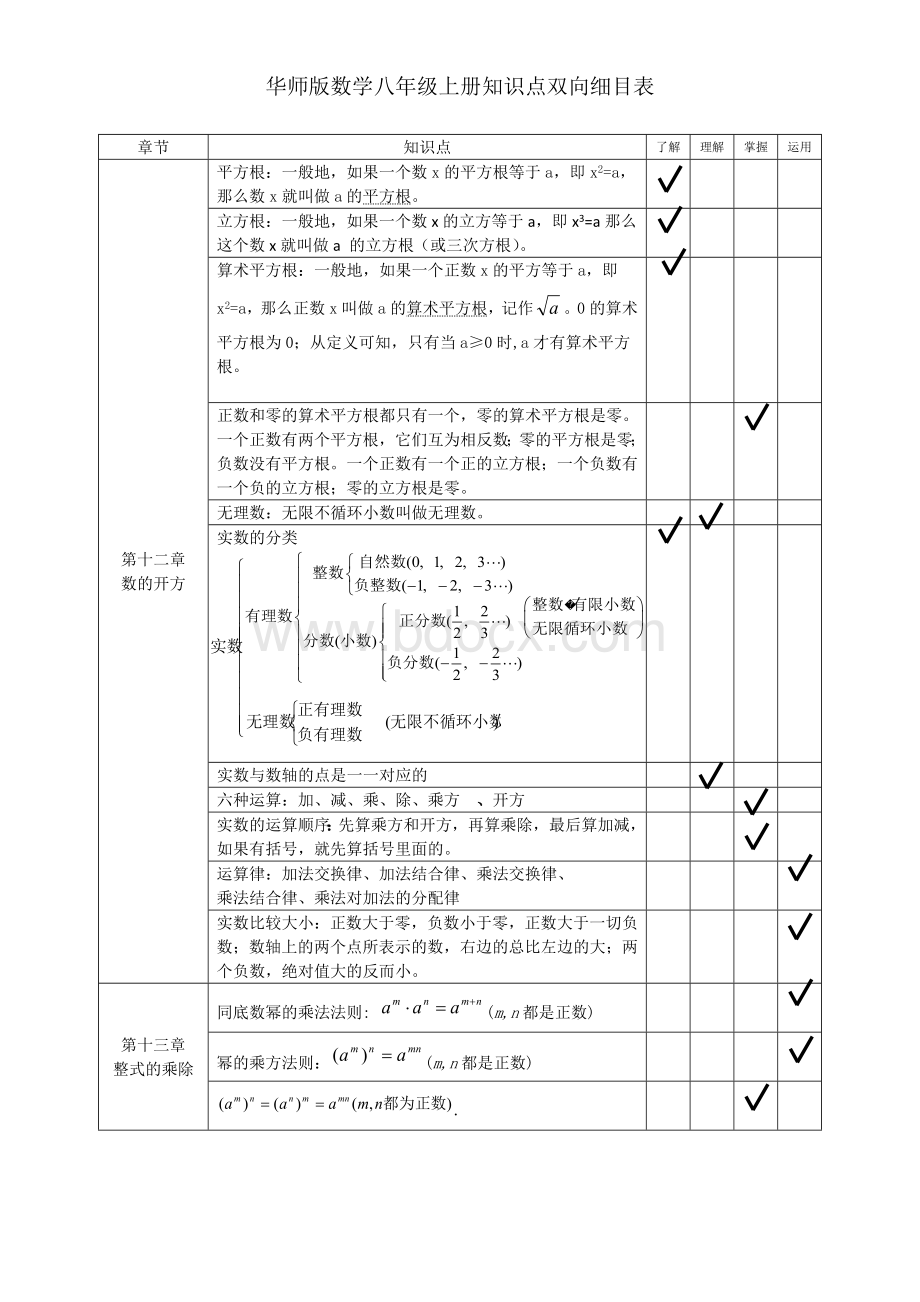
华师版数学八年级上册知识点双向细目表

章节

知识点

了解

理解

掌握

运用

第十二章

数的开方

平方根：

一般地，如果一个数x的平方根等于a，即x2=a，那么数x就叫做a的平方根。

立方根：

一般地，如果一个数x的立方等于a，即x3=a那么这个数x就叫做a的立方根（或三次方根）。

算术平方根：

一般地，如果一个正数x的平方等于a，即x2=a，那么正数x叫做a的算术平方根，记作。

0的算术平方根为0；从定义可知，只有当a≥0时,a才有算术平方根。

正数和零的算术平方根都只有一个，零的算术平方根是零。

一个正数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

无理数：

无限不循环小数叫做无理数。

实数的分类

实数与数轴的点是一一对应的

六种运算：

加、减、乘、除、乘方、开方

实数的运算顺序：

先算乘方和开方，再算乘除，最后算加减，如果有括号，就先算括号里面的。

运算律：

加法交换律、加法结合律、乘法交换律、

乘法结合律、乘法对加法的分配律

实数比较大小：

正数大于零，负数小于零，正数大于一切负数；数轴上的两个点所表示的数，右边的总比左边的大；两个负数，绝对值大的反而小。

第十三章

整式的乘除

同底数幂的乘法法则:

（m,n都是正数）

幂的乘方法则：

（m,n都是正数）

.

章节

知识点

了解

理解

掌握

运用

第十三章

整式的乘除

（a+b）n≠an+bn（a、b均不为零）。

积的乘方法则：

（n为正整数）。

同底数幂的除法法则:

同底数幂相除,底数不变,指数相减,即（a≠0,m、n都是正数,且m>n）.

任何不等于0的数的0次幂等于1,即

单项式乘法法则:

单项式相乘,把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，连同它的指数作为积的一个因式。

单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。

多项式与多项式相乘，先用一个多项式中的每一项乘以另一个多项式的每一项，再把所得的积相加。

平方差公式：

两数和与这两数差的积，等于它们的平方差，

即。

完全平方公式：

两数和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍，即口决：

首平方，尾平方，2倍乘积在中央；

单项式除以单项式：

单项式相除，把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式；

多项式除以单项式，先把这个多项式的每一项除以单项式，再把所得的商相加，

把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式.

因式分解与整式乘法是互逆关系

如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式.这种分解因式的方法叫做提公因式法.如:

如果把乘法公式反过来,就可以用来把某些多项式分解因式.这种分解因式的方法叫做运用公式法.

主要公式:

（1）平方差公式:

（2）完全平方公式:

利用分组来分解因式的方法叫做分组分解法.如:

二次三项式的分解:

章节

知识点

了解

理解

掌握

运用

第十三章

整式的乘除

对于二次三项式,将a和c分别分解成两个因数的乘积,,,且满足,往往写成的形式,将二次三项式进行分解.

如:

第十四章

勾股定理

勾股定理：

直角三角形两直角边a，b的平方和等于斜边c的平方，即

勾股定理的逆定理：

如果三角形的三边长a，b，c有关系，那么这个三角形是直角三角形。

勾股数：

满足的三个正整数，称为勾股数。

第十五章

平移与旋转

定义：

在平面内，将一个图形整体沿某方向移动一定的距离，这样的图形运动称为平移。

性质：

平移前后两个图形是全等图形，对应点连线平行且相等，对应线段平行且相等，对应角相等。

定义：

在平面内，将一个图形绕某一定点沿某个方向转动一个角度，这样的图形运动称为旋转，这个定点称为旋转中心，转动的角叫做旋转角。

性质：

旋转前后两个图形是全等图形，对应点到旋转中心的距离相等，对应点与旋转中心的连线所成的角等于旋转角。

定义：

图形绕着某一定点旋转一定的角度后能与自身重合的图形称为旋转对称图形。

定义：

在平面内，一个图形绕某个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

性质：

（1）关于中心对称的两个图形是全等形。

（2）关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

（3）关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。

判定：

如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。

两个图形通过翻折、平移和旋转能够完全重合的两个图形叫做全等图形

一个图形经过翻折、平移和旋转等变换所得到的新图形一定与原图形全等；反过来，两个全等的图形经过上述变换后一定能够互相重合。

章节

知识点

了解

理解

掌握

运用

第十五章

平移与旋转

如果两个多边形是全等图形，也成为全等多边形，两个全等的多边形，经过变换而重合，相互重合的顶点叫做对应顶点，相互重合的边叫做对应边，相互重合的角叫做对应角。

性质：

全等多边形的对应边相等、对应角相等。

判定：

边、角分别对应相等的两个多边形全等。

性质：

全等三角形的对应边相等、对应角相等。

判定：

如果两个三角形的边、角分别对应相等，那么这两个三角形全等。

用轴对称、平移和旋转及其组合进行简单图案设计。

第十六章

平行四边形的认识

平行四边形的定义：

两组对边分别平行的四边形叫做平行四边形。

平行四边形的性质

（1）平行四边形的对边平行且相等。

（2）平行四边形相邻的角互补，对角相等

（3）平行四边形的对角线互相平分。

（4）平行四边形是中心对称图形，对称中心是对角线的交点。

若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段的中点是对角线的交点，并且这条直线二等分此平行四边形的面积。

推论：

夹在两条平行线间的平行线段相等。

平行四边形的判定

（1）定义：

两组对边分别平行的四边形是平行四边形

（2）定理1：

两组对角分别相等的四边形是平行四边形

（3）定理2：

两组对边分别相等的四边形是平行四边形

（4）定理3：

对角线互相平分的四边形是平行四边形

（5）定理4：

一组对边平行且相等的四边形是平行四边形

两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线的距离。

平行线间的距离处处相等。

平行四边形的面积：

S平行四边形=底边长×高=ah

矩形的定义：

有一个角是直角的平行四边形叫做矩形。

矩形的性质

（1）矩形的对边平行且相等

（2）矩形的四个角都是直角

（3）矩形的对角线相等且互相平分

（4）矩形既是中心对称图形又是轴对称图形；对称中心是对角线的交点（对称中心到矩形四个顶点的距离相等）；对称轴有两条，是对边中点连线所在的直线。

矩形的判定

（1）定义：

有一个角是直角的平行四边形是矩形

（2）定理1：

有三个角是直角的四边形是矩形

（3）定理2：

对角线相等的平行四边形是矩形

章节

知识点

了解

理解

掌握

运用

第十六章

平行四边形的认识

矩形的面积：

S矩形=长×宽=ab

菱形的定义：

有一组邻边相等的平行四边形叫做菱形

菱形的性质

（1）菱形的四条边相等，对边平行

（2）菱形的相邻的角互补，对角相等

（3）菱形的对角线互相垂直平分，并且每一条对角线平分一组对角

（4）菱形既是中心对称图形又是轴对称图形；对称中心是对角线的交点（对称中心到菱形四条边的距离相等）；对称轴有两条，是对角线所在的直线。

菱形的判定

（1）定义：

有一组邻边相等的平行四边形是菱形

（2）定理1：

四边都相等的四边形是菱形

（3）定理2：

对角线互相垂直的平行四边形是菱形

菱形的面积：

S菱形=底边长×高=两条对角线乘积的一半

正方形的定义：

有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。

正方形的性质

（1）正方形四条边都相等，对边平行

（2）正方形的四个角都是直角

（3）正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分一组对角

（4）正方形既是中心对称图形又是轴对称图形；对称中心是对角线的交点；对称轴有四条，是对角线所在的直线和对边中点连线所在的直线。

正方形的判定

判定一个四边形是正方形的主要依据是定义，途径有两种：

先证它是矩形，再证它是菱形。

先证它是菱形，再证它是矩形。

正方形的面积：

设正方形边长为a，对角线长为b

S正方形=

梯形的相关概念：

一组对边平行而另一组对边不平行的四边形叫做梯形。

梯形中平行的两边叫做梯形的底，通常把较短的底叫做上底，较长的底叫做下底。

梯形中不平行的两边叫做梯形的腰。

梯形的两底的距离叫做梯形的高。

梯形的判定

（1）定义：

一组对边平行而另一组对边不平行的四边形是梯形。

（2）一组对边平行且不相等的四边形是梯形。

章节

知识点

了解

理解

掌握

运用

第十六章

平行四边形的认识

一般地，梯形的分类如下：

一般梯形

梯形直角梯形

特殊梯形

等腰梯形

等腰梯形的定义：

两腰相等的梯形叫做等腰梯形。

等腰梯形的性质

（1）等腰梯形的两腰相等，两底平行。

（2）等腰梯形同一底上的两个角相等，同一腰上的两个角互补。

（3）等腰梯形的对角线相等。

（4）等腰梯形是轴对称图形，它只有一条对称轴，即两底的垂直平分线。

等腰梯形的判定

（1）定义：

两腰相等的梯形是等腰梯形

（2）定理：

在同一底上的两个角相等的梯形是等腰梯形

（3）对角线相等的梯形是等腰梯形。

（选择题和填空题可用）

梯形的面积:

（1）如图，

（2）梯形中有关图形的面积：

①；

②；

③

有关中点四边形问题的知识点：

（1）顺次连接任意四边形的四边中点所得的四边形是平行四边形；

（2）顺次连接矩形的四边中点所得的四边形是菱形；

（3）顺次连接菱形的四边中点所得的四边形是矩形；

（4）顺次连接等腰梯形的四边中