完整word版精讲精练因式分解方法分类总结培优含答案Word文档格式.docx
《完整word版精讲精练因式分解方法分类总结培优含答案Word文档格式.docx》由会员分享,可在线阅读,更多相关《完整word版精讲精练因式分解方法分类总结培优含答案Word文档格式.docx(36页珍藏版)》请在冰豆网上搜索。
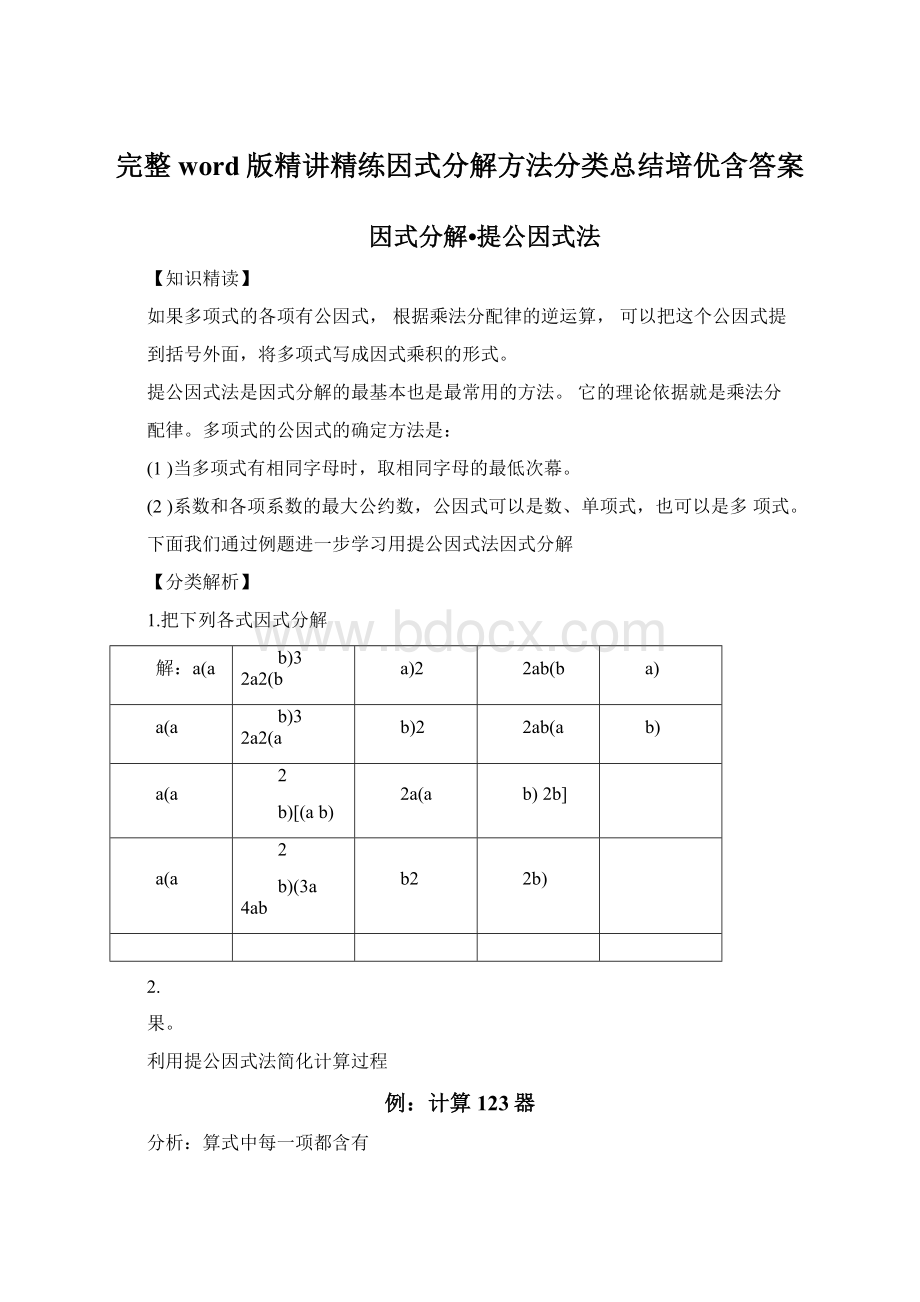
2m2m1mm3m23
axabxacxaxax(axbxcx)
(2)有时将因式经过符号变换或将字母重新排列后可化为公因式,如:
当n
为自然数时,(ab)2n(ba)2n;
(ab)2n1(ba)2n1,是在因式分解过
3.在多项式恒等变形中的应用
2xy3例:
不解方程组,求代数式(2xy)(2x3y)3x(2xy)的
5x3y2
值。
不要求解方程组,我们可以把2xy和5x3y看成整体,它们的值分
别是3和2,观察代数式,发现每一项都含有2xy,利用提公因式法把代数式
恒等变形,化为含有2xy和5x3y的式子,即可求出结果。
程中常用的因式变换。
(2xy)(2x3y)3x(2xy)(2xy)(2x3y3x)(2xy)(5x3y)
把2xy和5x3y分别为3和2带入上式,求得代数式的值是6。
4.在代数证明题中的应用
证明:
对于任意自然数n,3n22n23n2n一定是10的倍数。
首先利用因式分解把代数式恒等变形,接着只需证明每一项都是10的
倍数即可。
3门22门23门2门
3门23介2n22门
3n(321)2n(221)
nn
10352
对任意自然数n,10
3n和52n都是10的倍数。
3n22“23“2“
一定是10的倍数
5、中考点拨:
例1。
因式分解3x(x2)(2x)
3x(x2)(2x)
3x(x2)(x2)
(x2)(3x1)
说明:
因式分解时,应先观察有没有公因式,若没有,看是否能通过变形转换
得到。
例2•分解因式:
4q(1p)32(p1)2
32
4q(1p)2(p1)
4q(1p)2(1p)
2(1P)2[2q(1p)1]
2(1p)2(2q2pq1)
在用提公因式法分解因式前,必须对原式进行变形得到公因式,同时一
定要注意符号,提取公因式后,剩下的因式应注意化简。
题型展示:
例1•计算:
200020012001200120002000
精析与解答:
设2000a,则2001a1
a[10000(a1)(a1)](a1)(10000aa)
a(a1)10001a(a1)10001
a(a1)(1000110001)
此题是一个有规律的大数字的运算,若直接计算,运算量必然很大。
其
中2000、2001重复出现,又有200120001的特点,可通过设未知数,将复
杂数字间的运算转化为代数式,再利用多项式的因式分解化简求值,从而简化计算。
例2.已知:
x2bxc(b、c为整数)是x46x225及3x44x228x5
的公因式,求b、c的值。
常规解法是分别将两个多项式分解因式,求得公因式后可求b、c,但
比较麻烦。
注意到x2bxc是3(x46x225)及3x44x228x5的因式。
因而也是(3x44x228x5)的因式,所求问题即可转化为求这个多项式的二
次因式。
x2bxc是3(x46x225)及3x44x228x5的公因式
4242
也是多项式3(x6x25)(3x4x28x5)的二次因式
42422
而3(x6x25)(3x4x28x5)14(x2x5)
b、c为整数
得:
x2bxcx22x5
b2,c5
这是对原命题进行演绎推理后,转化为解多项式14x228x70,从
而简便求得xbxc。
x2,5x都是大于1的自然数
(x2)(5x)是合数
在大于1的正数中,除了1和这个数本身,还能被其它正整数整除的数叫合数。
只能被1和本身整除的数叫质数。
【实战模拟】
1.分解因式:
(1)4m2n312m3n22mn
(2)a2xn2abxn1acxnadxn1(n为正整数)
(3)a(ab)32a2(ba)22ab(ba)2
2.计算:
(2)11
(2)10的结果是(
)
J00
A.2
B.2
C.2
D.1
3.已知x、y都是正整数,且x(xy)y(yx)12,求x、y。
7913
4.证明:
81279能被45整除。
例3•设x为整数,试判断105xx(x2)是质数还是合数,请说明理由。
105xx(x2)
21995
5.化简:
1xx(1x)x(1x)…x(1x),且当x0时,求原式
5(2x)x(x2)
(x2)(5x)
的值。
试题答案
1.分析与解答:
(1)4m2n312m3n22mn
22
2mn(2mn6mn1)
2n
(2)ax
2.n1
1
acx
nn1
adx
n
1/3
.2
ax
(ax
bx
cx
d)
(3)
原式
b)3
2a2
(ab)2
2ab(ab)
[(a
b)2a
2b]
(3a
3b)
3a(a
注意:
结果多项因式要化简,同时要分解彻底。
2.B
3.x(xy)y(yx)12
(xy)(xy)12
x、y是正整数
12分解成112,26,34
x
y2
y6
4
y
求不定方程的整数解,
经常运用因式分解来解决。
817279913
小28小27小26
333
26
3(931)
3265
亠24亠2一
335
32445
817
913
279能被45整除
5.解:
逐次分解:
原式(1
x)(1
x)
x(1x)2
…x(1
、1995
(1
x)2(1
…x(1x)
1995
x)3(1
x(1x)4
1996
(1x)
当x0时,原式1
又xy与xy奇偶性相同,且xyxy
因式分解•公式法
C.(ab)(ab)2
D.(a22b)(b22a)
把乘法公式反过来,就可以得到因式分解的公式。
主要有:
平方差公式
a2
(a
b)(a
完全平方公式
2ab
立方和、立方差公式
b3
b)(a
abb)
补充:
欧拉公式:
a3b3
c33abc
(ab
222
c)(abc
abbcca)
特别地:
(1)当a
(2)当
a2ab2b
a2a1b2b
再利用平方差公式进行分解,最后得到
1(a1)(b1)。
(ab)(ab2),故选择B。
解这类题目时,一般先观察现有项的特征,通过添加项凑成符合公式的形式。
同时要注意分解一定要彻底。
2.在简便计算、求代数式的值、解方程、判断多项式的整除等方面的应用
已知多项式2xxm有一个因式是2x1,求m的值。
12
2(abc)[(ab)2
bc0时,有a3b3
c0时,欧拉公式变为两数立方和公式。
(bc)2(ca)2]
运用公式法分解因式的关键是要弄清各个公式的形式和特点,熟练地掌握公
式。
但有时需要经过适当的组合、变形后,方可使用公式。
用公式法因式分解在求代数式的值,解方程、几何综合题中也有广泛的应用。
因此,正确掌握公式法因式分解,熟练灵活地运用它,对今后的学习很有帮助。
F面我们就来学习用公式法进行因式分解
1•把a2ab2b分解因式的结果是
由整式的乘法与因式分解互为逆运算,可假设另一个因式,再用待定系
数法即可求出m的值。
根据已知条件,设2x3
x2m(2x1)(x2axb)
A.(ab)(a2)(b2)
B.(ab)(ab2)
则2xx
m2x(2a1)x(a2b)xb
2a11
(1)
由此可得a2b0
(2)
mb(3)
由
(1)得a1
把a1代入
(2),得b-
11
把b-代入(3),得m—
3.在几何题中的应用。
已知a、b、c是ABC的三条边,且满足
abcabbcac0,试判断ABC的形状。
因为题中有a、b、ab,考虑到要用完全平方公式,首先要把ab
转成2ab。
所以两边同乘以2,然后拆开搭配得完全平方公式之和为0,从而得
解。
a2b
2c
ab
bc
ac0
2b2
2c2
2bc
2ac0
(a2
(b2
c)(c2aca)0
(b
c)2
(c
0,
(ca)20
a
b0,
b
c
0,<
ca
abc
ABC为等边三角形。
4.在代数证明题中应用
两个连续奇数的平方差一定是8的倍数。
先根据已知条件把奇数表示出来,然后进行变形和讨论。
设这两个连续奇数分别为2n1,2n3(n为整数)
则(2n3)2(2n1)2
(2n32n1)(2n32n1)
2(4n4)
8(n1)
由此可见,(2n3)2(2n1)2一定是8的倍数。
例1:
因式分解:
x4xy。
_
3222解:
x4xyx(x4y)x(x2y)(x2y)
因式分解时,先看有没有公因式。
此题应先提取公因式,再用平方差公
式分解彻底。
3223
例2:
分解因式:
2xy8xy8xy。
3223222
2xy8xy8xy2xy(x4xy4y)2xy(x2y)
先提取公因式,再用完全平方公式分解彻底。
题型展示:
例1.已知:
1m
1,
b討2,c
3,
求a22ab
2ac
c22bc的值。
若b0或c0,同理也有a5b5c50
利用补充公式确定a,b,c的值,命题得证。
a22abb22acc22bc
22(ab)2c(ab)c
(abc)2
…1C
1门
m
1,bm2,c
m3
bc)2
2
(1m1)(1m2)(丄m3)
本题属于条件求值问题,解题时没有把条件直接代入代数式求值,而是
把代数式因式分解,变形后再把条件带入,从而简化计算过程。
例2.已知abcO,abc0,
求证:
a5b5c50
a3b3c33abc(a
bc)(a2b2c2abbcca)
把a
3,33
bc0,abc
0代入上式,
例3.若x3
3
27,
xxy
9,求xy的值。
x3
(x
y)(x2
xy
y2)
27
且x2xy
9
xy
3,x2
2xyy2
又x2xy
两式相减得
所以x2y29
按常规需求出x,y的值,此路行不通。
用因式分解变形已知条件,简化计算过程。
可得abc0,即a0或b0或c0若a0,则bc,
1.
(1)(a2)2(3a1)2
原式[(a2)(3a1)][(a2)(3a1)]
(4a1)(2a3)
(4a1)(2a3)
3.若a,b,c是三角形的三条边,求证:
a2b2c22bc0
分析与解答:
由于对三角形而言,需满足两边之差小于第三边,因此要证明结论就需要把问题转化为两边差小于第三边求得证明。
x5(x2y)x2(2y
解:
52
x5(x2y)x2(x
2y)
x2(x2y)(x31)
x(x2y)(x1)(xx
1)
a(xy)2a(x
\3
y)
(xy)4
(xy)2[a22a(x
(xy)2]
把a2,3a1看成整体,利用平方差公式分解。
(xy)2(axy)2
a2b2c22bc
a2(b22bcc2)
a2(bc)2
(abc)(abc)
a,b,c是三角形三边
abc0且abc
即a2
4.
已知:
bc)(a
bc)0
2bc0
0,求2001的值。
1)(
1)0,即3
丄)2
2x
If
27
2(3)
(x2
)2
49,
41
x4
249
x4447
2.已知:
X—3,求X4—的值。
5.
2001
(3)667
已知a,
b,c是不全相等的实数,且
(1)abc的值;
(2)a(-b
abc0,
c(」
c33abc,试求
-)的值。
说明:
(2)所求代数式较复杂,考虑恒等变形。
(1)由因式分解可知
a3b3c33abc(abc)(a2b2c2
故需考虑abcabbcca值的情况
[3bc(bc)]abc
1(3abc)abc
因式分解与配方法是在代数式的化简与求值中常用的方法。
因式分解•分组分解法
分组分解法的原则是分组后可以直接提公因式,或者可以直接运用公式。
使用这种方法的关键在于分组适当,而在分组时,必须有预见性。
能预见到下一步能继
续分解。
而“预见”源于细致的“观察”,分析多项式的特点,恰当的分组是分组分解法的关键。
应用分组分解法因式分解,不仅可以考察提公因式法,公式法,同时它在代数
式的化简,求值及一元二次方程,函数等学习中也有重要作用。
下面我们就来学习用分组分解法进行因式分解。
1.在数学计算、化简、证明题中的应用
例1.把多项式2a(a2a1)a4a21分解因式,所得的结果为()
2222
A.(aa1)B.(aa1)
C.(aa1)D.(aa1)
先去括号,合并同类项,然后分组搭配,继续用公式法分解彻底。
原式2a((a2
a1)a4a21
a4
2a3
3a2
2a1
(a4
a2)
(2a22a)1
2(a2
a)1
29
(aa1)
故选择C
例2.分解因式x5x4x3x2x1x5x4x3和x2x1分别看成一组,此时六项式变成二项式,提取公因式后,再进一步分解;
此题也可把x5x4,x3x2和x1分别看作一组,此时的六项式变成三项式,提取公因式后再进行分解。
解法1:
原式(x5
x4
3、
x)
(x3
1)(x2
解法2:
x4)
x2)
x4(x1)
x2(x1)
1)(x4
1)[(x
2x
21)
]
2.在几何学中的应用
已知三条线段长分别为a、b、c,且满足ab,a2c2b22ac
以a、b、c为三边能构成三角形
构成三角形的条件,即三边关系定理,是“两边之和大于第三边,两边之差小于第三边”
a2c2b22ac
这是一个六项式,很显然要先进行分组,此题可把
a2c2b22ac0
a22acc2b20,即(ac)2b20
(acb)(acb)0
又acbacb
acb0,acb0
abc,abc
即abcab
3.在方程中的应用
求方程xyxy的整数解
这是一道求不定方程的整数解问题,直接求解有困难,因等式两边都含
有x与y,故可考虑借助因式分解求解
xyxy
xyxy0
xyxy11
即x(y1)(y1)1
(y1)(x1)1
x,y是整数
x11x11
或
y11y11
x0x2
y0y2
4、中考点拨
例1•分解因式:
1m2n22mn
1m2n22mn
1(m22mnn2)
1(mn)2
(1mn)(1mn)
观察此题是四项式,应采用分组分解法,中间两项虽符合平方差公式,但搭配在一起不能分解到底,应把后三项结合在一起,再应用完全平方公式和平方
差公式。
例2.分解因式:
xyxy
x2y2xy(x2y2)(xy)
(xy)(xy)(xy)
(xy)(xy1)
前两项符合平方差公式,把后两项结合,看成整体提取公因式。
例3.分解因式:
x33x24x12
3232
x3x4x12x4x3x12
x(x24)3(x24)
(x3)(x2)(x2)
分组的目的是能够继续分解。
5、题型展示:
例1.分解因式:
m2(n21)4mnn21
个因式。
222,2,
mnm4mnn1
(mn2mn1)(m2mnn)
(mn1)(mn)
(mnmn1)(mnmn1)
观察此题,直接分解比较困难,不妨先去括号,再分组,把
2mn和2mn,配成完全平方和平方差公式。
4mn分成
例2.已知:
a2b2
1,c2d2
1,且acbd
0,求ab+cd的值。
ab+cd=ab1ab(c2abc2
cd1
d2)cd(a2
abd2cda2
b2)
cdb2
(abc2
cdb)(abdcda)
bc(ac
bd)ad(bdac)
(acbd)(bcad)
acbd0
原式0
首先要充分利用已知条件
a2b21,c2d21中的(任何数乘以1,
其值不变),其次利用分解因式将式子变形成含有ac+bd因式乘积的形式,由
ac+b