中考数学专题复习转化与归化思想的解题策略与应试技巧+考前押题含答案.docx

中考数学专题复习转化与归化思想的解题策略与应试技巧+考前押题含答案.docx

《中考数学专题复习转化与归化思想的解题策略与应试技巧+考前押题含答案.docx》由会员分享，可在线阅读，更多相关《中考数学专题复习转化与归化思想的解题策略与应试技巧+考前押题含答案.docx（30页珍藏版）》请在冰豆网上搜索。

中考数学专题复习转化与归化思想的解题策略与应试技巧+考前押题含答案

数学思想方法

转化与化归思想

类型十一“一般”与“特殊”之间的转化

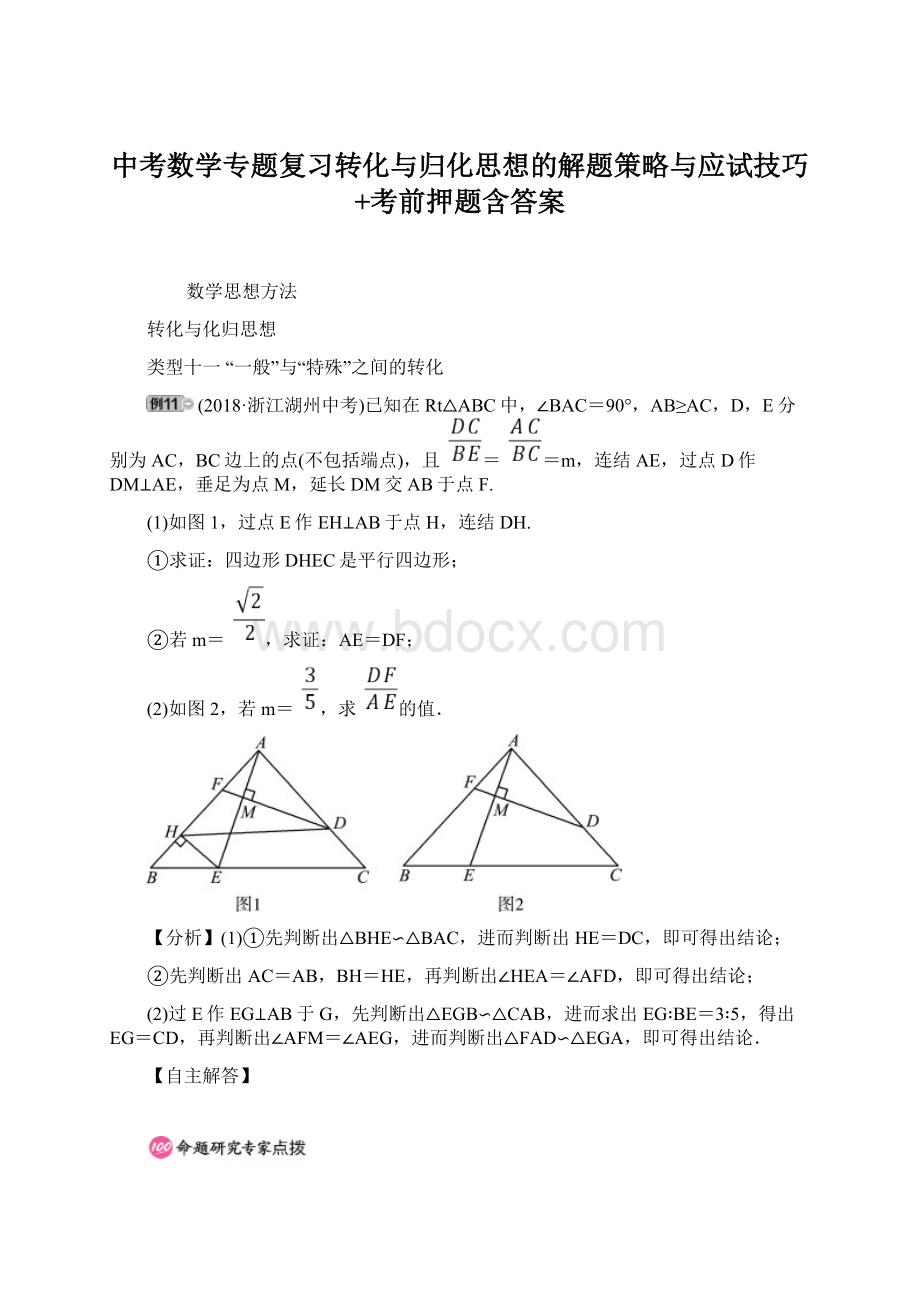
（2018·浙江湖州中考）已知在Rt△ABC中，∠BAC＝90°，AB≥AC，D，E分别为AC，BC边上的点（不包括端点），且＝＝m，连结AE，过点D作DM⊥AE，垂足为点M，延长DM交AB于点F.

（1）如图1，过点E作EH⊥AB于点H，连结DH.

①求证：

四边形DHEC是平行四边形；

②若m＝，求证：

AE＝DF；

（2）如图2，若m＝，求的值．

【分析】

（1）①先判断出△BHE∽△BAC，进而判断出HE＝DC，即可得出结论；

②先判断出AC＝AB，BH＝HE，再判断出∠HEA＝∠AFD，即可得出结论；

（2）过E作EG⊥AB于G，先判断出△EGB∽△CAB，进而求出EG∶BE＝3∶5，得出EG＝CD，再判断出∠AFM＝∠AEG，进而判断出△FAD∽△EGA，即可得出结论．

【自主解答】

从特殊到一般，从具体到抽象是研究数学的一种基本方法．在一般情况下难以发现的规律，在特殊条件下容易暴露，特殊情况下得出的结论、方法也往往可以推广到一般情形．所以，特殊与一般之间的转化，可以用来验证命题的正确性，探索解题途径．

12．（2018·广西桂林中考）如图，在平面直角坐标系中，M，N，C三点的坐标分别为（，1），（3，1），（3，0），点A为线段MN上的一个动点，连结AC，过点A作AB⊥AC交y轴于点B，当点A从M运动到N时，点B随之运动．设点B的坐标为（0，b），则b的取值范围是（）

A.－≤b≤1B．－≤b≤1

C．－≤b≤D．－≤b≤1

13．（2018·甘肃陇南中考）如图，⊙A过点O（0，0），C（，0），D（0，1），点B是x轴下方⊙A上的一点，连结BO，BD，则∠OBD的度数是（）

A．15°B．30°C．45°D．60°

类型十二“复杂”与“简单”之间的转化

（2018·浙江台州中考）解不等式组：

【分析】根据不等式组的解集的表示方法：

大小小大中间找，可得答案．

【自主解答】

数学解题的过程是分析问题和解决问题的过程，对于较复杂的问题．可以通过分析，将问题转化为几个简单的问题来解决，如把“多元问题”转化为“一元问题”、把“高次问题”转化为“一次问题”、把“分式问题”转化为“整式问题”等，实现复杂问题简单化．

14．（2018·四川遂宁中考）如图，已知抛物线y＝ax2－4x＋c（a≠0）与反比例函数y＝的图象相交于B，且B点的横坐标为3，抛物线与y轴交于点C（0，6），A是抛物线y＝ax2－4x＋c（a≠0）的顶点，P点是x轴上一动点，当PA＋PB最小时，P点的坐标为____________．

类型十三“生活”与“数学”之间的转化

（2018·浙江绍兴中考）如图1，窗框和窗扇用“滑块铰链”连结，图3是图2中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，交点A处装有滑块，滑块可以左右滑动，支点B，C，D始终在一直线上，延长DE交MN于点F.已知AC＝DE＝20cm，AE＝CD＝10cm，BD＝40cm.

（1）窗扇完全打开，张角∠CAB＝85°，求此时窗扇与窗框的夹角∠DFB的度数；

（2）窗扇部分打开，张角∠CAB＝60°，求此时点A，B之间的距离（精确到0.1cm）．（参考数据：

≈1.732，≈2.449）

【分析】

（1）根据平行四边形的性质和判定可以解答本题；

（2）根据锐角三角函数可以求得AB的长，从而可以解答本题．

【自主解答】

数学是人们生活、劳动和学习必不可少的工具，能够帮助人们处理数据、进行计算、推理和证明，数学模型可以有效地描述自然现象和社会现象．所以，要重视数学知识的应用．在解决实际问题时，要重在分析，把实际问题转化为数学模型，以提高应用数学知识解决实际问题的能力．

15．（2018·浙江绍兴中考）实验室里有一个水平放置的长方体容器，从内部量得它的高是15cm，底面的长是30cm，宽是20cm，容器内的水深为xcm.现往容器内放入如图的长方体实心铁块（铁块一面平放在容器底面），过顶点A的三条棱的长分别10cm，10cm，ycm（y≤15），当铁块的顶部高出水面2cm时，x，y满足的关系式是___________________________________．

类型十四“数”与“形”之间的转化

（2018·四川德阳中考）已知函数y＝使y＝a成立的x的值恰好只有3个时，a的值为________．

【分析】首先在坐标系中画出已知函数y＝的图象，利用数形结合的方法即可找到使y＝a成立的x值恰好有3个的a值．

【自主解答】

“数”与“形”反映了事物两方面的属性，数与形之间的相互转化、相互联系，体现了数学是一个有机整体．数形结合能把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，是一条合理的解题途径．

16．（2018·江苏泰州中考）平面直角坐标系xOy中，二次函数y＝x2－2mx＋m2＋2m＋2的图象与x轴有两个交点．

（1）当m＝－2时，求二次函数的图象与x轴交点的坐标；

（2）过点P（0，m－1）作直线l⊥y轴，二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上），求m的范围；

（3）在

（2）的条件下，设二次函数图象的对称轴与直线l相交于点B，求△ABO的面积最大时m的值．

参考答案

类型十一

【例11】

（1）①∵EH⊥AB，∠BAC＝90°，

∴EH∥CA，∴△BHE∽△BAC，

∴＝.

∵＝，∴＝，

∴＝，∴HE＝DC.

∵EH∥DC，∴四边形DHEC是平行四边形．

②∵＝，∠BAC＝90°，∴AC＝AB.

∵＝，HE＝DC，∴＝.

∵∠BHE＝90°，∴BH＝HE.

∵HE＝DC，∴BH＝CD，∴AH＝AD.

∵DM⊥AE，EH⊥AB，

∴∠EHA＝∠AMF＝90°，

∴∠HAE＋∠HEA＝∠HAE＋∠AFM＝90°，

∴∠HEA＝∠AFD.

∵∠EHA＝∠FAD＝90°，

∴△HEA≌△AFD，∴AE＝DF.

（2）如图，过点E作EG⊥AB于G.

∵CA⊥AB，∴EG∥CA，

∴△EGB∽△CAB，∴＝，

∴＝＝.

∵＝，∴EG＝CD.

设EG＝CD＝3x，AC＝3y，

∴BE＝5x，BC＝5y，∴BG＝4x，AB＝4y.

∵∠EGA＝∠AMF＝90°，

∴∠GEA＋∠EAG＝∠EAG＋∠AFM，

∴∠AFM＝∠AEG.

∵∠FAD＝∠EGA＝90°，

∴△FAD∽△EGA，

∴＝＝＝.

变式训练

12．B　13.B

类型十二

【例12】

解不等式①得x＜4，

解不等式②得x＞3，

不等式①，不等式②的解集在数轴上表示如图．

原不等式组的解集为3＜x＜4.

变式训练

14．（，0）　

类型十三

【例13】

（1）∵AC＝DE＝20cm，

AE＝CD＝10cm，

∴四边形ACDE是平行四边形，

∴AC∥DE，∴∠DFB＝∠CAB.

∵∠CAB＝85°，∴∠DFB＝85°.

（2）如图，作CG⊥AB于点G.

∵AC＝20，∠CGA＝90°，∠CAB＝60°，

∴CG＝10，AG＝10.

∵BD＝40，CD＝10，∴CB＝30，

∴BG＝＝10，

∴AB＝AG＋BG＝10＋10≈10＋10×2.449＝34.49≈34.5cm，

即A，B之间的距离为34.5cm.

变式训练

15．y＝（0＜x≤）或y＝（6≤x＜8）

类型十四

【例14】函数y＝的图象如图，

根据图象知，当y＝2时，对应成立的x值恰好有三个，

∴a＝2.故答案2.

变式训练

16．解：

（1）当m＝－2时，抛物线表达式为y＝x2＋4x＋2.

令y＝0，则x2＋4x＋2＝0，

解得x1＝－2＋，x2＝－2－，

抛物线与x轴交点坐标为（－2＋，0），（－2－，0）．

（2）∵y＝x2－2mx＋m2＋2m＋2＝（x－m）2＋2m＋2，

∴抛物线顶点坐标为A（m，2m＋2）．

∵二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上），

∴当直线l在x轴上方时，

不等式无解．

当直线l在x轴下方时，

解得－3＜m＜－1.

（3）由

（1）点A在点B上方，则AB＝（2m＋2）－（m－1）＝m＋3，

△ABO的面积S＝（m＋3）（－m）＝－m2－m.

∵－＜0，

∴当m＝－＝－时，S最大＝.

综合性压轴题

类型一函数中点的存在性问题

（2018·山东东营中考）如图，抛物线y＝a（x－1）（x－3）（a＞0）与x轴交于A，B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC.

（1）求线段OC的长度；

（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的表达式；

（3）在

（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？

若存在，请求出点P的坐标；若不存在，请说明理由．

【分析】

（1）令y＝0，求出x的值，确定出A与B坐标，根据已知相似三角形得比例，求出OC的长即可；

（2）根据C为BM的中点，利用直角三角形斜边上的中线等于斜边的一半得到OC＝BC，确定出C的坐标，利用待定系数法确定出直线BC的表达式，把C坐标代入抛物线求出a的值，确定出二次函数的表达式即可；

（3）过P作x轴的垂线，交BM于点Q，设出P与Q的横坐标为x，分别代入抛物线与直线表达式，表示出纵坐标，相减表示出PQ，四边形ACPB面积最大即为三角形BCP面积最大，三角形BCP面积等于PQ与B和C横坐标之差乘积的一半，构造为二次函数，利用二次函数性质求出此时P的坐标即可．

【自主解答】

1．（2018·湖南衡阳中考）如图，已知直线y＝－2x＋4分别交x轴、y轴于点A，B，抛物线经过A，B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D.

（1）若抛物线的表达式为y＝－2x2＋2x＋4，设其顶点为M，其对称轴交AB于点N.

①求点M，N的坐标；

②是否存在点P，使四边形MNPD为菱形？

并说明理由；

（2）当点P的横坐标为1时，是否存在这样的抛物线，使得以B，P，D为顶点的三角形与△AOB相似？

若存在，求出满足条件的抛物线的表达式；若不存在，请说明理由．

类型二图形运动中的函数关系问题

如图，在△ABC中，AB＝6cm，AC＝4cm，BC＝2cm，点P以1cm/s的速度从点B出发沿边BA→AC运动到点C停止，运动时间为ts，点Q是线段BP的中点．

（1）若CP⊥AB时，求t的值；

（2）若△BCQ是直角三角形时，求t的值；

（3）设△CPQ的面积为S，求S与t的关系式，并写出t的取值范围．

【分析】

（1）作CH⊥AB于H.设BH＝x，利用勾股定理构建方程求出x，当点P与H重合时，CP⊥AB，此时t＝2；

（2）分两种情形求解即可解决问题；

（3）分两种情形讨论，求出QM即可解决问题．

【自主解答】

2．（2018·广东中考）已知Rt△OAB，∠OAB＝90°，∠ABO＝30°，斜边OB＝4，将Rt△OAB绕点O顺时针旋转60°，如图1，连结BC.

（1）填空：

∠OBC＝°；

（2）如图1，连结AC，作OP⊥AC，垂足为P，求OP的长度；

（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN