基于matlab的霍夫变换Word格式.docx
《基于matlab的霍夫变换Word格式.docx》由会员分享,可在线阅读,更多相关《基于matlab的霍夫变换Word格式.docx(10页珍藏版)》请在冰豆网上搜索。
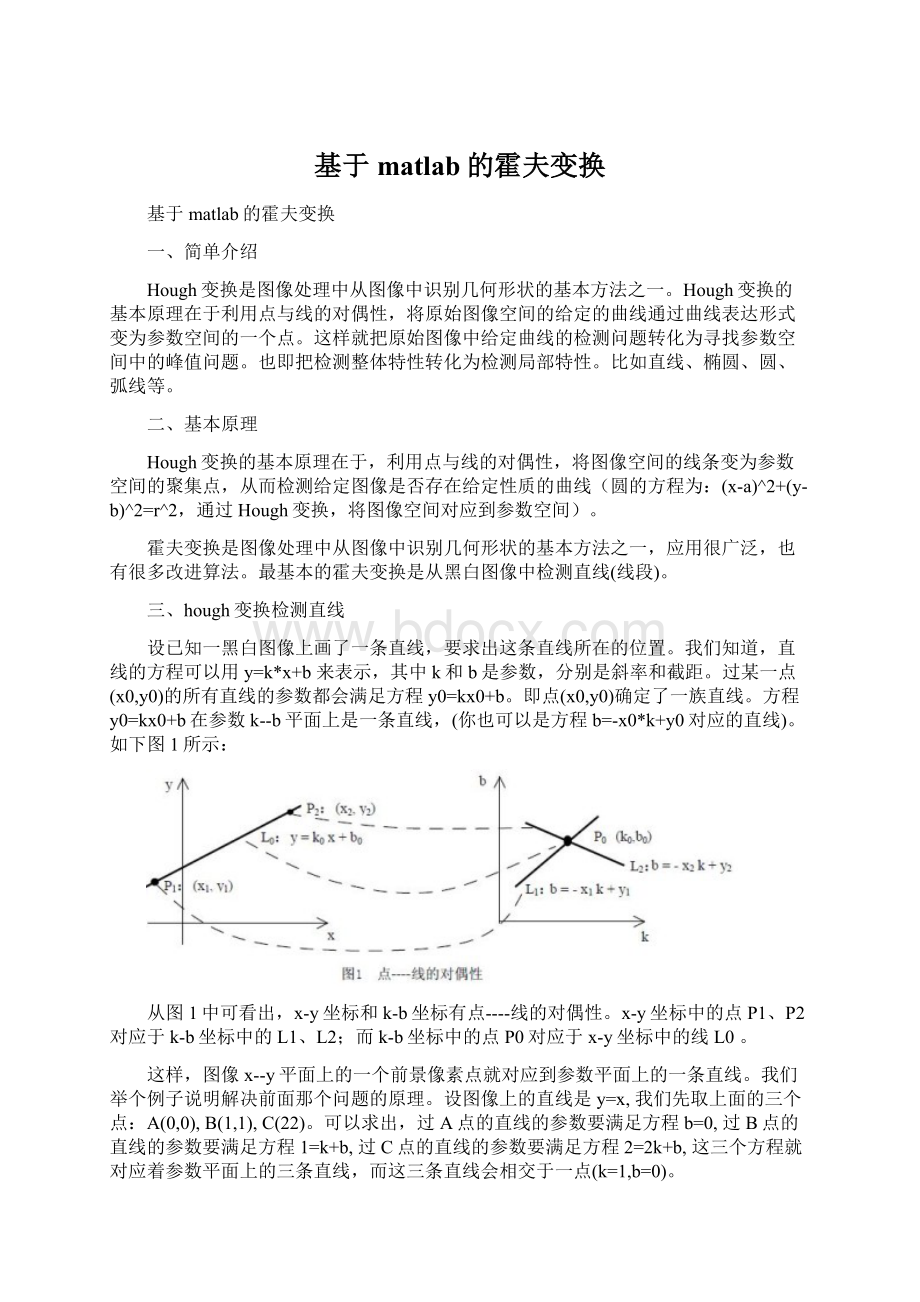
这样在将原始坐标系下的各个点投影到参数坐标系下之后,看参数坐标系下有没有聚集点,这样的聚集点就对应了原始坐标系下的直线。
这个性质就为我们解决问题提供了方法:
首先,我们初始化一块缓冲区,对应于参数平面,将其所有数据置为0。
然后,对于图像上每一前景点,求出参数平面对应的直线,把这直线上的所有点的值都加1。
最后,找到参数平面上最大点的位置,这个位置就是原图像上直线的参数。
上面就是霍夫变换的基本思想。
就是把图像平面上的点对应到参数平面上的线,最后通过统计特性来解决问题。
在实际应用中,y=k*x+b形式的直线方程没有办法表示x=c形式的直线(这时候,直线的斜率为无穷大)。
所以实际应用中,是采用参数方程p=x*cos(theta)+y*sin(theta)。
这样,图像平面上的一个点就对应到参数p---theta平面上的一条曲线上。
其它的还是一样。
在极坐标a-p中变为一条正弦曲线,a取(0-180°
)。
可以证明,直角坐标X-Y中直线上的点经过Hough变换后,它们的正弦曲线在极坐标a-p有一个公共交点,如图2所示:
也就是说,极坐标a-p上的一点(a,p),对应于直角坐标X-Y中的一条直线,而且它们是一一对应的。
为了检测出直角坐标X-Y中由点所构成的直线,可以将极坐标a-p量化成许多小格。
根据直角坐标中每个点的坐标(x,y),在a=0-180°
内以小格的步长计算各个p值,所得值落在某个小格内,便使该小格的累加记数器加1。
当直角坐标中全部的点都变换后,对小格进行检验,计数值最大的小格,其(a,p)值对应于直角坐标中所求直线。
四、hough变换检测圆
再看下面一个问题:
我们要从一副图像中检测出半径以知的圆形来。
这个问题比前一个还要直观。
我们可以取和图像平面一样的参数平面,以图像上每一个前景点为圆心,以已知的半径在参数平面上画圆,并把结果进行累加。
最后找出参数平面上的峰值点,这个位置就对应了图像上的圆心。
在这个问题里,图像平面上的每一点对应到参数平面上的一个圆。
把上面的问题改一下,假如我们不知道半径的值,而要找出图像上的圆来。
这样,一个办法是把参数平面扩大称为三维空间。
就是说,参数空间变为x--y--R三维,对应圆的圆心和半径。
图像平面上的每一点就对应于参数空间中每个半径下的一个圆,这实际上是一个圆锥。
最后当然还是找参数空间中的峰值点。
不过,这个方法显然需要大量的内存,运行速度也会是很大问题。
有什么更好的方法么?
我们前面假定的图像都是黑白图像(二值图像),实际上这些二值图像多是彩色或灰度图像通过边缘提取来的。
我们前面提到过,图像边缘除了位置信息,还有方向信息也很重要,这里就用上了。
根据圆的性质,圆的半径一定在垂直于圆的切线的直线上,也就是说,在圆上任意一点的法线上。
这样,解决上面的问题,我们仍采用2维的参数空间,对于图像上的每一前景点,加上它的方向信息,都可以确定出一条直线,圆的圆心就在这条直线上。
这样一来,问题就会简单了许多。
接下来还有许多类似的问题,如检测出椭圆,正方形,长方形,圆弧等等。
这些方法大都类似,关键就是需要熟悉这些几何形状的数学性质。
霍夫变换的应用是很广泛的,比如我们要做一个支票识别的任务,假设支票上肯定有一个红颜色的方形印章,我们可以通过霍夫变换来对这个印章进行快速定位,在配合其它手段进行其它处理。
霍夫变换由于不受图像旋转的影响,所以很容易的可以用来进行定位。
霍夫变换有许多改进方法,一个比较重要的概念是广义霍夫变换,它是针对所有曲线的,用处也很大。
就是针对直线的霍夫变换也有很多改进算法,比如前面的方法我们没有考虑图像上的这一直线上的点是否连续的问题,这些都要随着应用的不同而有优化的方法。
五、程序实现(圆)
上文中提到了检测圆的切线的方法,这里暂且不讨论,这里讨论经典HOUGH算法。
下面为我写的利用极坐标表示圆的一种算法流程:
1.图像灰度化,二值化(注意:
二值化的好坏对检测结果有很大影响,常用的有SOBEL算子)
2.检测图像中的边缘点,并保存其坐标位置。
设置角度theta的变化范围和步长,半径r的变换范围和步长。
3.利用公式x=a+rcos(theta),y=b+rsin(theta)求出a和b的值。
(注意:
x和y为实际的图像空间某个边缘点的坐标,a和b为其对应的参数空间的坐标),如果a和b的值在合理的范围之类,则对该位置进行累加。
例如:
[cpp]
viewplaincopy
1.for
i=1:
ecount
2.
for
r=1:
size_r
3.
k=1:
size_angle
4.
a
=
round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));
5.
b
round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));
6.
if(a>
0&
a<
=m&
b>
b<
=n)
7.
hough_space(a,b,r)
hough_space(a,b,r)+1;
8.
end
9.
10.
11.end
4.检索完毕,寻找最大值,求出圆心坐标与半径,保存。
1.function
[hough_space,hough_circle,para]
hough_circle(BW,step_r,step_angle,r_min,r_max,p);
2.%[HOUGH_SPACE,HOUGH_CIRCLE,PARA]
HOUGH_CIRCLE(BW,STEP_R,STEP_ANGLE,R_MAX,P)
3.%------------------------------算法概述-----------------------------
4.%
该算法通过a
x-r*cos(angle),b
y-r*sin(angle)将圆图像中的边缘点
5.%
映射到参数空间(a,b,r)中,由于是数字图像且采取极坐标,angle和r都取
6.%
一定的范围和步长,这样通过两重循环(angle循环和r循环)即可将原图像
7.%
空间的点映射到参数空间中,再在参数空间(即一个由许多小立方体组成的
8.%
大立方体)中寻找圆心,然后求出半径坐标。
9.%-------------------------------------------------------------------
11.%------------------------------输入参数-----------------------------
12.%
BW:
二值图像;
13.%
step_r:
检测的圆半径步长
14.%
step_angle:
角度步长,单位为弧度
15.%
r_min:
最小圆半径
16.%
r_max:
最大圆半径
17.%
p:
以p*hough_space的最大值为阈值,p取0,1之间的数
18.%-------------------------------------------------------------------
19.
20.%------------------------------输出参数-----------------------------
21.%
hough_space:
参数空间,h(a,b,r)表示圆心在(a,b)半径为r的圆上的点数
22.%
hough_circl:
二值图像,检测到的圆
23.%
para:
检测到的圆的圆心、半径
24.%-------------------------------------------------------------------
25.
26.%
From
Internet,Modified
by
mhjerry,2011-12-11
27.
28.[m,n]
size(BW);
29.size_r
round((r_max-r_min)/step_r)+1;
30.size_angle
round(2*pi/step_angle);
31.
32.hough_space
zeros(m,n,size_r);
33.
34.[rows,cols]
find(BW);
35.ecount
size(rows);
36.
37.%
Hough变换
38.%
将图像空间(x,y)对应到参数空间(a,b,r)
39.%
x-r*cos(angle)
40.%
y-r*sin(angle)
41.for
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.end
52.
53.%
搜索超过阈值的聚集点
54.max_para
max(max(max(hough_space)));
55.index
find(hough_space>
=max_para*p);
56.length
size(index);
57.hough_circle=zeros(m,n);
58.for
59.
length
60.
par3
floor(index(k)/(m*n))+1;
61.
par2
floor((index(k)-(par3-1)*(m*n))/m)+1;
62.
par1
index(k)-(par3-1)*(m*n)-(par2-1)*m;
63.
if((rows(i)-par1)^2+(cols(i)-par2)^2<
(r_min+(par3-1)*step_r)^2+5&
...
64.
(rows(i)-par1)^2+(cols(i)-par2)^2>
(r_min+(par3-1)*step_r)^2-5)
65.
hough_circle(rows(i),cols(i))
1;
66.
67.
68.end
69.
70.%
打印结果
71.for
72.
73.
74.
75.
r_min+(par3-1)*step_r;
76.
fprintf(1,'
Center
%d
radius
%d\n'
par1,par2,par3);
77.
para(:
k)
[par1,par2,par3]'
;
78.end
79.
六、总结
图像空间中的在同一个圆,直线,椭圆上的点,每一个点都对应了参数空间中的一个图形,在图像空间中这些点都满足它们的方程这一个条件,所以这些点,每个投影后得到的图像都会经过这个参数空间中的点。
也就是在参数空间中它们会相交于一点。
所以,当参数空间中的这个相交点的越大的话,那么说明元图像空间中满足这个参数的图形越饱满。
越象我们要检测的东西。
Hough变换能够查找任意的曲线,只要你给定它的方程。
Hough变换在检验已知形状的目标方面具有受曲线间断影响小和不受图形旋转的影响的优点,即使目标有稍许缺损或污染也能被正确识别。
【Circle2.bmp】
【完整代码如下】
%--2015/1/49:
56--%
f=imread('
circle2.bmp'
);
imshow(f);
f=rgb2gray(f);
[m,n]=size(f);
r_max=200;
r_min=1;
step_r=1;
size_r=round((r_max-r_min)/step_r)+1;
step_angle=1;
size_angle=round(2*pi/step_angle);
hough_space=zeros(m,n,size_r);
[rows,cols]=find(f);
ecount=size(rows);
fori=1:
ecount
forr=1:
size_r
fork=1:
size_angle
a=round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));
b=round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));
=n)
hough_space(a,b,r)=hough_space(a,b,r)+1;
end
max_para=max(max(max(hough_space)));
p=0.5;
index=find(hough_space>
=(max_para*p));
length=size(index);
hough_circle=zeros(m,n);
length
par3=floor(index(k)/(m*n))+1;
par2=floor((index(k)-(par3-1)*(m*n))/m)+1;
par1=index(k)-(par3-1)*(m*n)-(par2-1)*m;
if(((rows(i)-par1)^2+(cols(i)-par2)^2)<
((r_min+(par3-1)*step_r)^2+5)&
((rows(i)-par1)^2+(cols(i)-par2)^2)>
((r_min+(par3-1)*step_r)^2-5))
hough_circle(rows(i),cols(i))=1;
par3=r_min+(par3-1)*step_r;
center%d%dr=%d\n'
k)=[par1,par2,par3]'
输出结果是:
par1=205,par2=180,par3=174