微积分导数与微分典型例题与复习题部分解答Word文档下载推荐.docx
《微积分导数与微分典型例题与复习题部分解答Word文档下载推荐.docx》由会员分享,可在线阅读,更多相关《微积分导数与微分典型例题与复习题部分解答Word文档下载推荐.docx(30页珍藏版)》请在冰豆网上搜索。
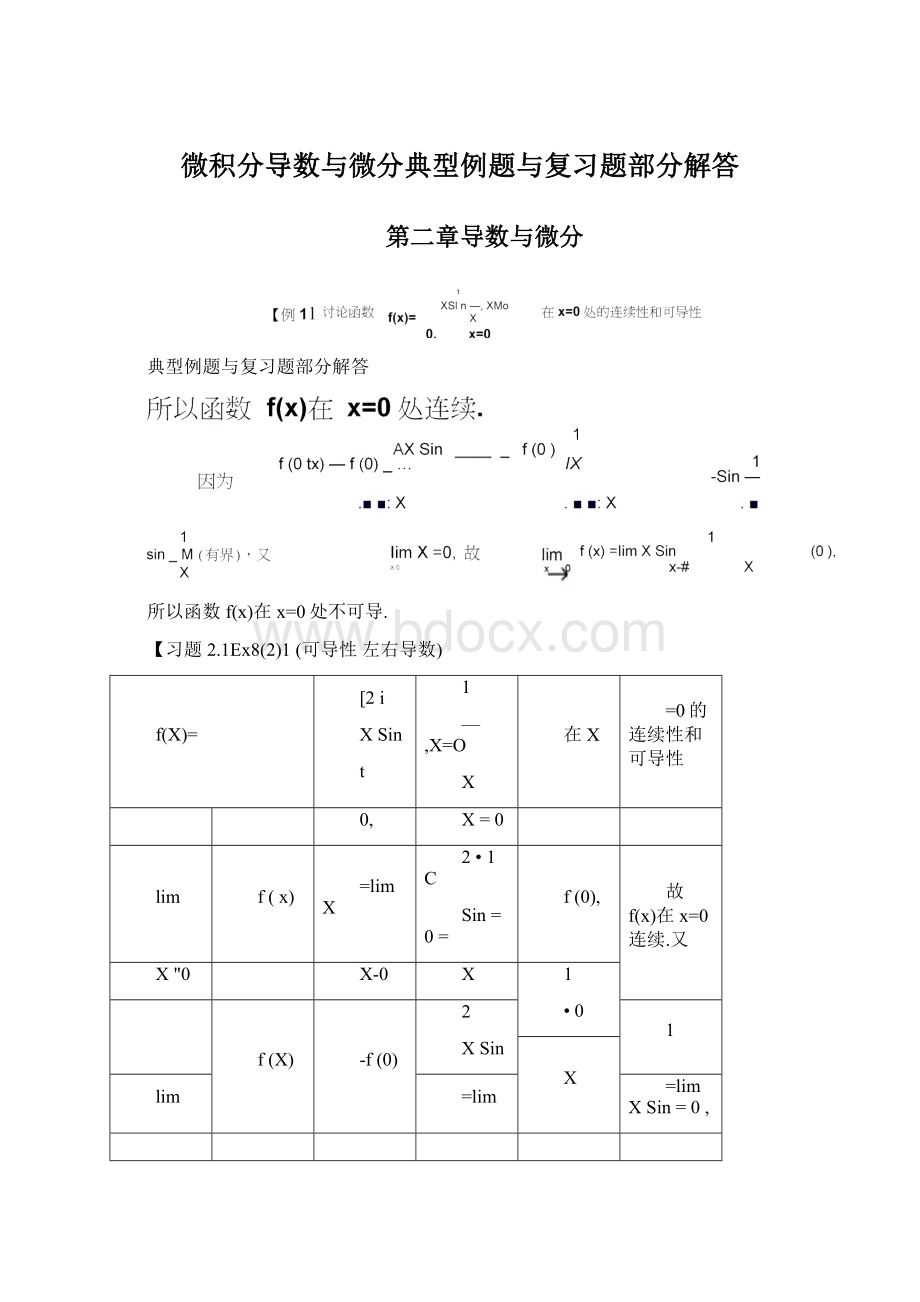
b=I
f
(1)=Iimf(x)
X)+
-a.而由导数存在性
=Iim(ax亠b)=a亠b,
X1亠
f.
(1)
f_
(1)
f(X)_f
(1)
=Iim
X_1'
X—1
f(X)_f
(1)
—Iim
X—1-X_1
a-2,b=_1.
(ax+b)_1ax_a
=IimIima,
x—1X_1■x—.1
(2)
X-1
X_1
-Iim一=Iim(XM^2.由
(1)、
(2)解得
x—.X_1X—1'
】
(书P44习题2.1Ex10)因f(x)在x=1处可导,故必连续,从而
1=f
(1)=limf(x)=Iim(ax亠b)=(ax亠b)|x」=a」b.
Xf+X)1+—
由此得当x≥1时f(x)=ax+b,且f'
x)=a;
又当x≤1时f'
(x)=2x.注意到两个导函数都是初等函数,故导函数在指定区域连续,特别是左(或,右)端点连续.于是由可导性得
a=f'
+
(1)=f'
(1)=(2x)∣x=1=2,
由此得b=-1.
【习题2.2Ex5(3)(5)(9)(10)】求下列函数的导函数:
解:
arcsinXarcsinX
(3)y=(e)=e
(arcsinX)
(5)
(9)
(10)
arcsin
二e
arcsinXe
1
y=(arccos—)
y=[ln(secX亠tan
x)]
222
y=(xa-X亠aarcsin
arcsinzXe
(x)__
1「(x)21一X2X2x-χ2
(1)
|xI
1一(:
)2
1一2
χ2丨x丨/1-丄
∖X
(SeCX亠tanx)(SeCx)亠(tanx)SeCXtan
Xsec2X
二SeCX.
SeCX亠tanX
SeCX亠tanX
X222X
—)=(XYa_x)亠a(arcsin—)=aa
2222∙2
-X-^x(a_x)亠a
(—)
a
X2
1—()
Ia
22F
(a-X)
X—
CJ2
2a
亠a2
-X
Ja)
22二2:
a-X
2222^a-X:
a-X
(10)
2X
亠aarcsin一)
(11)
Iry
=(5
X2
(12)
=(In
(a2-
2.a2
X2)
2X)=5
e
X)
1■e
/2
(Xa
—Z
(
)
.1一(
—
.a2-
)a
3亠a
22"
E-X2
a-X
(arcsin一)
2x2-2X
(X
2x)
=5
(2x2)=2(X1)5
1-e
1.^e
XXXX
e(1亠e)-ee
(1e)
【习题2.2Ex5(13)(14)(15)(16)】求下列函数的导函数:
(14)
111
—-InX—InXI
y二(Xx)二(ex)二ex(InX)
InX-X
InX-1
(15)
InX-In2X
)=(e
In2X2
=e(In
InX
=X2In
HInX」
X(InX)=X
(16)
Ha,X—a
y(arctan—■In.)
X-a
+
22
X-a
3
aa2a
+=
222244
aXaXa
(1)y'
=[f(1+√X)]"
=f"
(X+√Γ)(X+J"
=1fIx+J;
).
<
2(x丿
注:
f(x...X)=f(u)」X
(2)Y=f(ex)ef(XT=[f(ex)]ef(X)f(ex)[ef(X)]
=f(ex)(ex)ef(X)f(ex)ef(X)f(x)
=f(ex)exef(X)f(ex)ef(X)f(x)
^ef(X)[f(ex)exf(ex)f(x)].注:
f(ex)=f(u)∣u$
[f(3x)ΓfH(3x)(3xf3f*(3x)
(3)y=[arctanf(3x)]222
1+[f(3x)]1+[f(3x)]1+[f(3x)]
【习题2.2Ex7](论证题)设f(x)是可导的偶函数,证明L(X)奇函数.
证:
-X,由f为偶函数得f(-x)=f(x),两边求导得(-x)f(-x)=f(X),即P
f(-x)=-f(X),-X,
所以f(X)是奇函数.
【习题2.2Ex8](论证题)设f(x)是可导的奇函数,证明f(X)奇偶函数.
-X,由f为奇函数得f(-x)=-f(x),两边求导得(-x)f(-x)=-f(x),PP
f(-x)=f(X),X,
所以f(X)是偶函数.
【习题2.2Ex9](论证题)设f(x)是可导的偶函数,且「(0)存在,证明f(0)=0.
-X,由f为偶函数得f(-x)=f(x);
因f(0)存在,故
f(0)=0.
y=[ln(1
X2)]=
(1—X)
-2X
O(1-2
-X)-
-X(^-X)
〜X
(1-
(1
—X
)补2X
2(1U
22—
22.
(1_X
1-x
XXX
(2)y=(e-COS2x)=(e_)COS2x…e_(COS2X)
XX
=e-(—x)cos2X∙e-(—sin2x)(2x)
_X__X_x
=-e~cos2X亠e~(-2sin2x)=_e_(cos2x亠2sin2x),
F
y"
=-e~(cos2x亠2sin2X)
XtXIi
--[(e-)(cos2x^2sin2x)亠e_(cos2x亠2sin2x)]
XX
--[∙∙e-(cos2x亠2Sin2x)亠e_(-2Sin2x亠4cos2x)]
_x
=e~(4sin2x-3cos2x).
【习题2.3Ex1(5)(6)]求下列函数的二阶导函数:
y=[ln(X亠1亠X
H=(XrXS
2i
(1X)
1
21X
2x
121x2
1X2
X1χ2
•1X」
X-:
1X2
(IX
2—72
X)2(1X)
、.(1X2)3
(6)yy
1-X
=
—1
=一I2
I1+x」
I1+x丿
(1+X)
(1+x)J
2[(1X)]
4
(1X)
4(1x)4
4=3
(1X)(1X)
(2)y=(xe)=e
X22
=e(12x),
XXXx(e)eXe
(12x2
X22
=(e)(12x)
X2.2
二e(x)(12x)e
■4X
=e2x(12X)e4x=e(6X
【习题2.3Ex3
(1)-(3)1设f(x)可导,求下列函数的导函数:
⑴y'
=[f(χ2)]Jf(X2)(χb=2xf(x2).
2222222
y=[2xf(x)]=2[f(X)Xf(X)(X)=2[f(X)^2Xf(X)].
【习题2.3Ex5
(1)】求下列函数的n阶导函数:
(1)y=(Sin2X)=2SinX(SinX)=2SinXCOSX=Sin2x,
y
=(Sin2
X)
2cos2X:
-2sin(2X
π
-):
I
FFr
=(2cos
=-2Sin
2X=2sin(
),
(4)
H3
=-(2
Sin
X)=—2
cos2^=2
sin(
3),
(n)n_1∏
Y=2sin[2X,—(n-1)].2
【习题2.3Ex5
(2)-(4)】
(2)y=(a)=aIna,
XX2
y=(aIna)=aIna,
y=(axIn2a)=axIn3a,
y(n)=axInna.
djydy(bbss⅛ini)))bbcoostttbb
COPtttodXχdx((aa(CDlSS)Sl))Γ-LaaSsimtttaa
化简为
2丄2、
Xy
χ+yy'
=y-χy'
即y'
=_=1_2X,由此得
y+Xy十X
复习题二部分解答
1.填空题:
f[a_(1/h)]_f(a)
A=-Iimf'
(a).
h.:
:
-.1/h
f(2_Ax)_f
(2)1f(2_「:
x)_f
(2)1
(4)已知f'
(2)=2,贝UIimIimf'
(2)=_1.
⅛∙02Zx2⅛-0_^x2
(5)设f(x)=x(x+1)(x+2)…(x+n),
f'
(x)=(x+1)(x+2)…(x+n)+x(x+2)…(x+n)+…+x(x+1)(x+3)…(x+n).
由此得f'
(0)=n!
(6)设y=f(lnx)ef(X),其中f可微,则
3)(1X)-J
6.设函数f(x)=∣x-a∣(x),其中(x)在x=a处连续且(a)≠0.讨论f(x)在x=a处的可导性.
因lim』(X)=limLx一a®
(X)=©
(a),limf(x^lim|^a^(X^-φ(a),
XTXTX—a7—7—x—a
又f(a)≠0,故左右导数不等,从而f(x)在x=a处不可导.
7.求下列函数的导数
(1)y=axxa(a>
0,a≠1)
y'
(axxa)'
(ax)'
xa+ax(xα)'
(axlna)xα+ax(axα-1)=axxαlna+ax+1xα-1.
⑵y=f(f(x))+f(sin2x),其中f可导.
(2_x)3、[Jx+2(2_x)3]'
(1_x)5_[(1_x)5]'
Jχ+2(2_x)3
10
(1—X)
“、市f—(2—X)3—3(2—X)2(1—x)5+5(1—》<
右(2—X)
(1—x)|匕2X2
(2-x)3X2135
(1-X)5[2(x+2)2-X1-X
12cosX2
CSCXln(1SinX)-2=CSCXln(1SinX)1.SinXSinXSinX
8.求下列方程所确定的隐函数的导数dy.
(2)e2χ∙y-coS(Xy)=e-1∙
dX
原式两边对X取导数得e2x丁(2∙y'
)-Sin(Xy)(yxy'
)=0,由此得
dy2e2xy-ysin(Xy)
dxe2x+y+xsin(Xy)"
233
dx[(cost),]
222_
3costsint
(3sintcost),(7costsint)-(3Sintcost)(-3costsint),
【复习题二12】设某商品的需求函数为Q=150—2P2.
(1)求当价格P=6时的边际需求,并解释其经济意义;
(2)求当价格P=6时的需求价格弹性,解释经济意义;
(3)当价格P=6时若价格下降2%,总收益将变化百分之几?
是增加还是减少?
显然Q'
(P)=—4P.当P=6时,Q=78,Q'
(6)=—24.
(1)当P=6时,边际需求Q'
(6)=—24V0.其经济意义为:
在价格
P=6时,价格上涨(或下降)一个单位时,需求量Q将由78个单位起减少(或增加)24个单位商品.(小大→大小;
小小→大)
(2)当价格P=6时,需求价格弹性为
P672
二..Q'
(P)二…(_24)二1.85,
Q7839
即当P=6时,≈1.85>
1,该商品为高弹性商品;
这说明在价格P=6时,价格上涨(或下降)1%,需求量Q将从28个单位起减少(或增加)1.85%.此时边际收益
R'
P)>
0,提高价格会使总收益减少,降低价格会使总收益增加•
(3)商品销售总收益和边际收益分别为
R(P)=PQ(P)=150P—2P3,R'
P)=150—6P2.
由此得R(6)=468,R(6)=—66,从而P=6时的收益价格弹性为
P611
εRPR'
(P)(-66)=0.846,
∙rp≈—0.846<
0.这就是说,若价格下降(小小→大)
R46813
即当价格p=6时,收益价格弹性
2%,总收益将增加1.692%.
其它杂题(求函数的导数、微分,导数的应用)
【例1】求函数y=x2在点x=2处的导数。
f(2」)—f
(2)
解1:
f
(2)=limLJIim
匚Xr0LX.'
Xr0
解2:
或⑵判m疸(fg)fW)亠声3
lim(47X)=4。
4°
【例2】
XX_X_∙2
1一Sin设f(x)=X
0,
x:
二O
x=O
f(O)
=Iimf(X)一f(O)
x「0X-O
当X=O
时,;
L(X)
Iim
x—∙0
=(—
—)H
0=X
艸於々农222)=:
。
求「(;
)及厂(0).
12—SinX-O
=Iim
X-∙0
=Iim
χjX
XSin2X-SinX
SinX
—1;
2xy=sin2
1+X
y=Sin2是由
【例3】
X求dydx
y=sinU,
Hπ
f(―)
复合而成,
dydydydydUdu
_==TT
dXdXdudud&
22(ι1我X)Lt2G⅛x)
==ccosU
【例4】
((VxX)2'
dy
y=lntanX,求I
dx
2(1-X)
GQS
(1X)1X
函数y=lntanx是由y=lnu,u=tanX复合而成,
廉e@ec2XdxdxdUdudX
UUU
SinXGQSX
【例5】
y=eX,求
y=e是由
U
y=e
U复合而成,
【例6】
InSinX
求dx
d⅛y11
NnIPSinSfiX)攻尸三—n:
(SinX)H
ddxSinSXnX
CoSX=GQtX.SinX
【例7】y=J[-2χ,求—y.
12
dy=[(1-2χ2)3r=1(1_2x2)飞(1_2x2)dx3
-4x
33(1二x2)2
【例8】
y=Incos(ex),求dy.
fy-[Incos(ex)]:
—1[cos(ex)]
dxcos(e)
一⅛⅛⅜⅛e恋F⅛⅛e⅛⅜Qex)。
【例9】
sin1
^eX,
sin!
y=(ex)
求dy
(Sin一
Sinl=eX
COS丄∙1)H
Sin_Xe
COS—
【例10】y=SinnxSinnX(门为常数),求§
y_.dx
y=(Sinnx)Sinnx+Sinnx(Sinnx)
=ncosnxSinnx+sinnxnSinn∙jχ(Sinx)
=ncosnxSinnX+nsinnjxcosx
=nSinnJXsin(n+1)x.
【例11】求函数y=x3当x=2,ΔX=0.02时的微分。
先求函数在任意点X的微分,
dy=(x3)Δx=3x2ΔXo
再求函数当x=2,Δx=0.02时的微分,
dyA=3χ2AX=3^2^002=024°
'
∣x=2∕=0.O2x=2,^=0.02°
“5"
U^O
【例12】yT'
xcosx,求dy。
应用积的微分法则,得
dy=d(e1^XCOSX)=COSXd(e1JX)e1JXd(COSX)
=(COSX)e1'
x(-3dx)e1^x(-SinXdX)--e1°
x(3cosXSinx)dx°
【例13】在括号中填入适当的函数,使等式成立。
⑴d()=xdx;
(2)d()=costdt。
(1)因为d(x2)=2xdx,所以
111222111222111222
XaiIdX^-Cld((Xx)))==Zddi(((^XX))!
即dd(((-j«
x))=XdX。
22222'
222
一般地,有d(—X亠C)=XCX(C为任意常数)。
(2)因为d(sin■t)=CoStdt,所以
11.11.
co¾
o盟曲tdt=≡-dds(nn驱坏)三c∣d((—SjIn时t)。
因此d(一sin.,t∙C)=8S∙,tdt(C为任意常数)。
【例16】设Y=
■]:
1.X
一(1X)-(1一X)
HX
.(1-x)(1X)3
【例17】
(对数求导法)设y=χ(sinX)COSX,
2cotX
2(1+cosX
为求y'
0)J将χ=0代入方程
(1),得
3y(0)y(0)-36y(0)=0
将x=0代入原方程,得y(O)=0,将此代入(*)中得
y"
)=1
【例20】求由方程ey∙xy-e=0所确定的隐函数y的导数。
eyyy+Xy二0,
方程中每一项对
X求导得(ey)(xy)-(e)=(0):
即
yy(Xe-0)。
亠e
【例21】
(可导性求解分段函数之未知数)
J,当X乞1
设f(χ)=J+x,已知f(x)在x=1处可导,
aχ+b