概率论公式总结Word文件下载.docx

资源描述

概率论公式总结Word文件下载.docx

《概率论公式总结Word文件下载.docx》由会员分享，可在线阅读，更多相关《概率论公式总结Word文件下载.docx（14页珍藏版）》请在冰豆网上搜索。

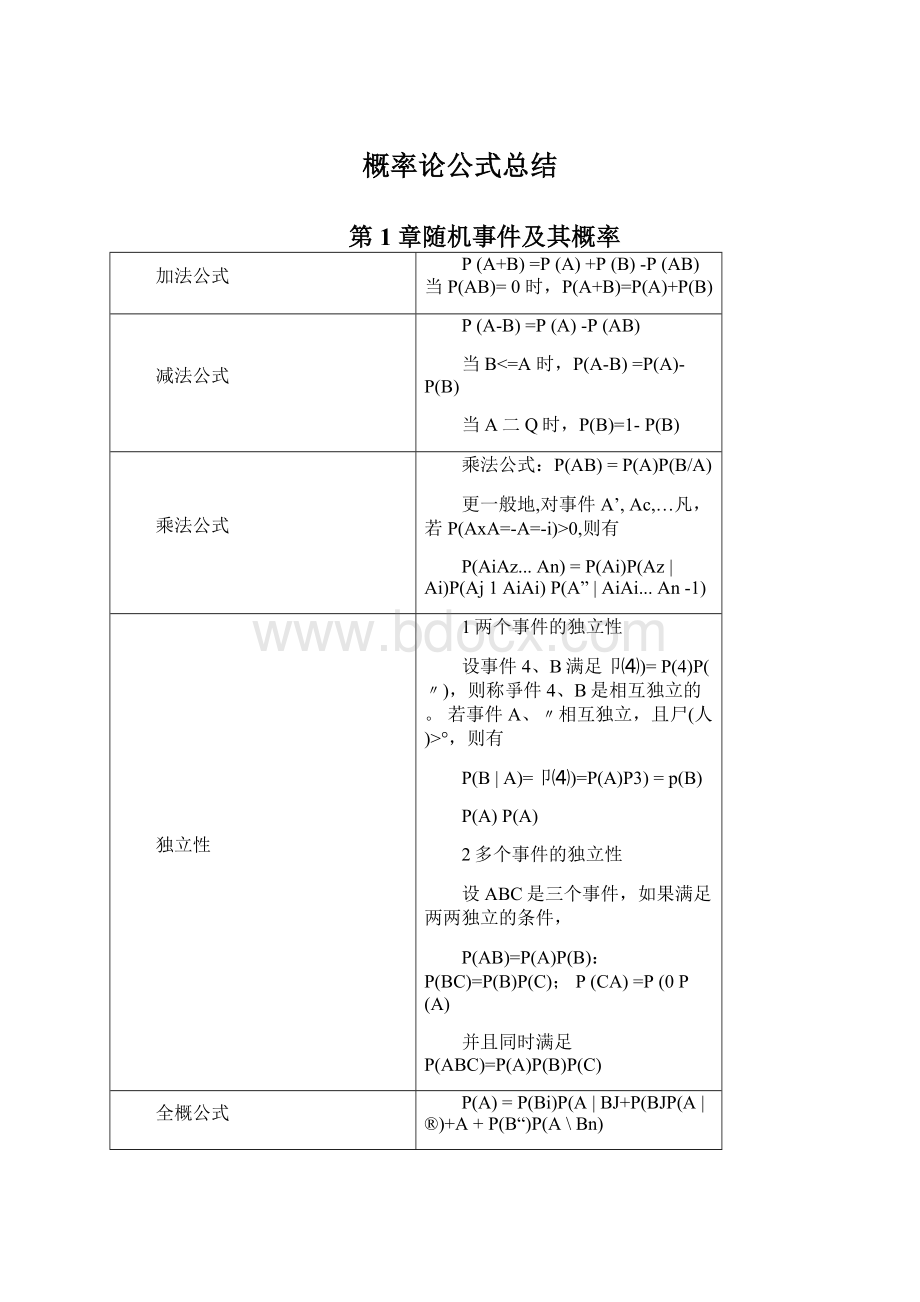
概率论公式总结Word文件下载.docx

称为X的概率密度函数或密度函数，简称概率密度。

密度函数具冇下面性质：

/（X）X°

L‘⑴办=1

离散与连续型随机变量的关系

P（X=x）^P（x<

x+dx）^f（x）dx枳分元f（x）clx/£

连续型随机变虽理论o

中所起的作用与P（X=汕）=Pk左离散型随机变虽理论中所起的作用相类似。

设X为随机变量，x是任意实数，则函数F（x）=P（X<

x）称为随机变量X的分布函数，本质上是一个累枳函数。

P（a<

b）=F（b）-F'

（a）可以得到X落入区间（a,b］的概率。

分布函数F（x）表示随机变量落入区间（・«

x］内的概率。

1.0<

F（x）<

1,—8VXV+S；

2。

F（x）是单调不减的函数，即xl<

X2时，有

尸（xi）<

Fg）；

3oF（-qo）=lullF（x）=0,F（+qo）=lullF（x）=1:

4。

XT-3C.V—HOC

尸（x+0）=F（x）,即F（x）是右连续的;

5.P（X=x）=F（x）-F（x-O）.对于离散型X

随机变量，对于连续型随机变量，。

=Jf\x）dx

-Ua—8

泊松分布

P（X=k）=^-e~\兄>

0.k=0,1,2A,

则称随机变量X服从参数为;

1的泊松分布，记为X〜兀（兄）或

者P

（2）o

超几何分布

PZk』・C：

*Z2Z

C；

1=mui（Af,/?

）

随机变量X服从参数为n,N,M的超几何分布，记为H（n,N,M）。

几何分布

p（X=k）=qZp、k=L23,A,其中pNO,q二1-p。

随机变量X服从参数为p的几何分布，记为G（p）°

均匀分布

设随机变量X的值只落在［a,b］内，其密度函数/（X）在［a,b］上为常数,1,即

•

f（x）=<

h-a^

0,其他

当aWxKx：

Wb时，X落在区间

（"

，心）内的概率为

P（X］<

Xvxj=——L

b—a

指数分布

正态分布

I0,兀<

其中久>

则称随机变量X服从参数为久的指数分布。

X的分布函数为

F（x）=

设随机变最X的密度两数为

两数分布

离散型

记住枳分公式

Jxne~'

dx=n\

1.（•"

其中"

、b>

为常数,则称随机变最X服从参数为"

、<

7的正态分布或高斯（Gauss）分布，记为X°

/（X）具有如下性质：

rf（x）的图形是关干x=p对称的：

2。

当时，/（//）=为最大值；

、J2"

若X~N（“,b）,则X的分布函数为

1厂吻弘F1厂*

①（X）是不可求积函数，其函数值,己编制成衣可供査用。

p（-x）=l-<

（x）且（D（0）=+。

如果X、则

~N（0,l）

Pg<

Xxz）

Xl.X2.A,Xn.A

P（X=x）

pi.PsA,pgA

己知X的分布列为

g（mg（r），A,g（Xn）,A

y=g（X）的分布列（”=g（xj互不相等）如下:

若:

某等，"

釦'

：

冷讪'

鋼"

偏加作为g（.®

的概率。

连续型

先利用X的概率密度fx（x）写出Y的分布函数Fv（y）=P（g（X）W

y）,再利用变上下限积分的求导公式求出fy（y）。

第三章二维随机变量及其分布

对于二维随机向量歹=（X』），如果存在非负函数

/（.V,y）（-s<

4-00,-00<

+s），使对任意一个其邻边分别平行于坐标轴的矩形区域D,即D={（X,Y）|a<

b,c<

有

P{（X,Y）6D}=j]7（x,y）dxdy,则称？

为连续型随机向量：

并称f（x,y）为歹二（X,Y）的分布密度或称为X和Y的联合分布密度。

分布密度f（x,y）具有下面两个性质：

（1）f（x,y）$0;

（2）匚匚f（x,y）dxdy=1.

离散型与连续型的关系

P（X=x,X=y）«

P（x<

x+dr,y<

Ky+dy）«

/（.v,y）dxdy

边缘分布

X的边缘分布为

・—P（X=兀）=工Ptj（i,j—1,2,A）:

Y的边缘分布为

p.j=p（丫=yj）=Pijo’J=1,2,a）。

〔:

型

X的边缘分布密度为

AW=J3/（"

）dy：

Y的边缘分布密度为fY（y）=匚/（利）力

Pq=Pi・P・j

有零不独立

f（x,y）=fx（x）fr（y）直接判断,充要条件:

①可分离变量②正概率密度区间为矩形

随机变量的

函数

若X：

…凡,j…人相互独立,h,g为连续函数，则：

h（Xx,X2,-X.）和g（人，・・％）相互独立。

特例：

若X与Y独立，则：

h（X）和区（Y）独立。

例如：

3X+1和5丫-2独立。

函数分布

Z=niaxjiini（

XX・・X』

才分布

t分布

根据定义计算：

rz（z）=p（z<

z）=p（x+r<

z）

态分布的和仍为正态分布（“i+M-cri+cr；

）。

n个相互独立的正态分布的线性组合，仍服从正态分布。

工以，宀工cp：

若X"

AX”相互独立，其分布函数分别为

FVi（x）tFx^（x）AFx（x）,则Z-max.iuui（Xi•*Xn）的分布

函数为：

FM）=行⑴•（x）AFXu（x）

Fmm（x）=1-[1-FXi（x）]•[!

-FXz（x）]A[1-FXk（x）]

设n个随机变量X],X"

A,X”相互独立，且服从标准正态分布，町以证明它们的平方和

W=fX：

我们称随机变SW服从自由度为n的Z2分布记为

1-1

W〜F（〃）

所谓门由度足指独X:

态随机变也的个数,它是随机变量分布

中的一个重要参数。

才分布满足可加性：

设Yj-x\nS则

Z=D〜力"

竹+公+A+nk）./■I

12X.Y是两个相互独立的随机变量，且X~N（Od）,Y~z2（/0,可

以证明函数T=-==我们称随机变量T服从自由度为n的t分布,

4y7h

记为T〜t（n）°

t^a（11）=-ta（7?

F分布

设X〜才〜才（心），且X与Y独立，可以证明F=X_ih_我们称随机变最f服从第一个自由度为m,第二个Yin.

自由度为n：

的F分布，记为F~f（m,m）.

e（w）-口t、

代⑺佔）

第四章随机变量的数字特征

期望

期望就是平均值

设X是离散型随机变最,其分布律为P（X=xk）=Pk,k=l,2,…，n,

（要求绝对收敛）

设X是连续型随机变量.其概率密度为f（x）,

■KC

E（X）=J#（x）dx

函数的期塑

Y=g（X）

砒）=£

gam

k=l

砒）=Jg（x）m）dx

-X

方差

D（X）=E[X-E（X）]:

标准差

6X）=J0X）,

D（X）=》E—E（X）]S

D（X）=][x-E（X）Y

-00

（1）E（C）二C

（2）E（CX）=CE（X）

（3）E（X+Y）=E（X）+E（Y）•E（工XJ=工CtE（XJ

（4）E（XY）=E（X）E（Y）,充分条件：

X和Y独立：

充要条件：

X和Y不相关。

f（x）dx

望性

随变的

⑴

-维机量数

字特征

（2）期的质

（3）方差的性质

（1）D（C）=O；

E（C）=C

（2）D（aX）=a：

D（X）；

E（aX）=aE（X）

（3）D（aX+b）=a：

D（X）:

E（aX+b）=aE（X）+b

（4）D（X）=E（X-）-E:

（X）

（5）D（X±

Y）=D（X）+D（Y）,充分条件:

X和Y独立；

D（X±

Y）=D（X）+D（Y）±

2E[（X-E（X））（Y-E（Y））],无条件成立。

而E（X+Y）二E（X）+E（Y）,无条件成立。

（4）常见分布的期望和方差

0-1分布3（1,p）

pQ-P）

二项分布B（n,p）

W（1-P）

泊松分布F（X）

几何分布G（p）

1一"

H0MN）

nML

n丿

均匀分布Ugb）

a+b

（b-a）2

指数分布讯刃

正态分布N（//,cr2）

力'

分布

—（n>

2）n-2

二维随机变量

E（X）=±

XjPi・

r=l

E（Y）二

E（X）=jxfx（x）dx

E（Y）=jyfY（y）dy

E[G（X.Y）]=工工G（兀，儿也

E[G（X,Y）]=

4CD+x

JJG（x,y）/（x,刃厶心

_X—QD

数字特征

d（x）=》[e-e（x）Fp・

-WC

D（X）=J[x-E（X）FA（x）dx

•wo

D（Y）=j[y-E（Y）]2fY（y）dy

协方差

对于随机变量X与Y.称它们的一阶混介中心矩为X与Y的协方差或相关矩,记为bxy或COV（X,K）,即

b灯=//11=^[（x-f（x）xy-E（n）].

与记号相对应，X与Y的方差D（X）与D（Y）也町分别记为丁茫与^YY。