届高三理科数学五年高考三年模拟分类汇编32 导数的应用Word格式文档下载.docx
《届高三理科数学五年高考三年模拟分类汇编32 导数的应用Word格式文档下载.docx》由会员分享,可在线阅读,更多相关《届高三理科数学五年高考三年模拟分类汇编32 导数的应用Word格式文档下载.docx(41页珍藏版)》请在冰豆网上搜索。
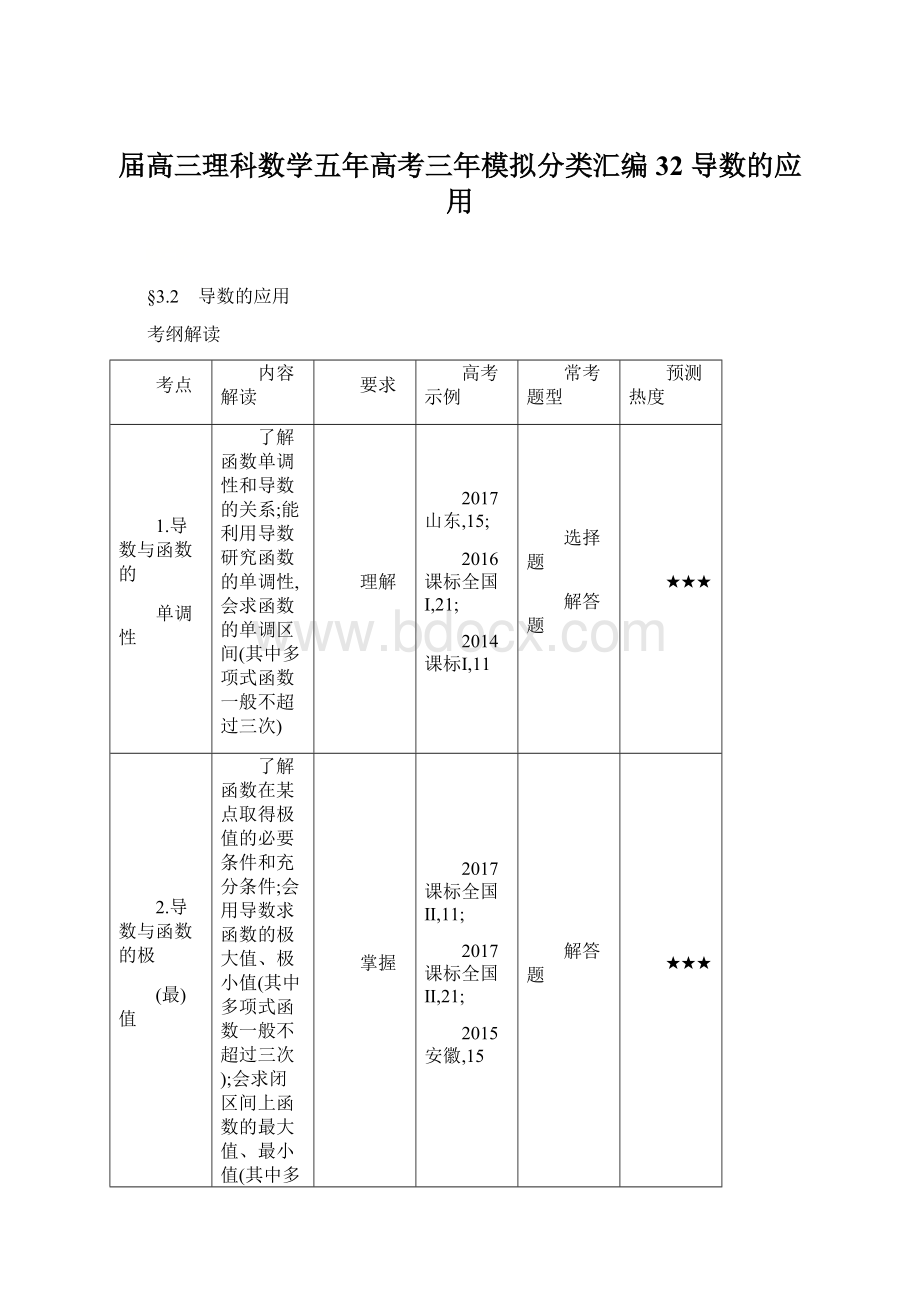
答案 C
3.(2017山东,15,5分)若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为 .
①f(x)=2-x ②f(x)=3-x ③f(x)=x3 ④f(x)=x2+2
答案 ①④
4.(2017江苏,11,5分)已知函数f(x)=x3-2x+ex-,其中e是自然对数的底数.若f(a-1)+f(2a2)≤0,则实数a的取值范围是 .
答案
5.(2017山东,20,13分)已知函数f(x)=x2+2cosx,g(x)=ex·
(cosx-sinx+2x-2),其中e=2.71828…是自然对数的底数.
(1)求曲线y=f(x)在点(π,f(π))处的切线方程;
(2)令h(x)=g(x)-af(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.
解析 本题考查导数的几何意义和极值.
(1)由题意f(π)=π2-2,
又f'
(x)=2x-2sinx,
所以f'
(π)=2π,
因此曲线y=f(x)在点(π,f(π))处的切线方程为y-(π2-2)=2π(x-π),即y=2πx-π2-2.
(2)由题意得h(x)=ex(cosx-sinx+2x-2)-a(x2+2cosx),
因为h'
(x)=ex(cosx-sinx+2x-2)+ex(-sinx-cosx+2)-a(2x-2sinx)
=2ex(x-sinx)-2a(x-sinx)
=2(ex-a)(x-sinx),
令m(x)=x-sinx,则m'
(x)=1-cosx≥0,
所以m(x)在R上单调递增.
因为m(0)=0,
所以当x>
0时,m(x)>
0;
当x<
0时,m(x)<
0.
①当a≤0时,ex-a>
0,
0时,h'
(x)<
0,h(x)单调递减,
当x>
(x)>
0,h(x)单调递增,
所以当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;
②当a>
(x)=2(ex-elna)(x-sinx),
由h'
(x)=0得x1=lna,x2=0.
a.当0<
a<
1时,lna<
当x∈(-∞,lna)时,ex-elna<
0,h'
0,h(x)单调递增;
当x∈(lna,0)时,ex-elna>
0,h(x)单调递减;
当x∈(0,+∞)时,ex-elna>
0,h(x)单调递增.
所以当x=lna时h(x)取到极大值,
极大值为h(lna)=-a[(lna)2-2lna+sin(lna)+cos(lna)+2],
当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;
b.当a=1时,lna=0,
所以当x∈(-∞,+∞)时,h'
(x)≥0,函数h(x)在(-∞,+∞)上单调递增,无极值;
c.当a>
1时,lna>
所以当x∈(-∞,0)时,ex-elna<
当x∈(0,lna)时,ex-elna<
当x∈(lna,+∞)时,ex-elna>
所以当x=0时h(x)取到极大值,极大值是h(0)=-2a-1;
当x=lna时h(x)取到极小值,
极小值是h(lna)=-a[(lna)2-2lna+sin(lna)+cos(lna)+2].
综上所述:
当a≤0时,h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,函数h(x)有极小值,极小值是h(0)=-2a-1;
当0<
1时,函数h(x)在(-∞,lna)和(0,+∞)上单调递增,在(lna,0)上单调递减,函数h(x)有极大值,也有极小值,
极大值是h(lna)=-a[(lna)2-2lna+sin(lna)+cos(lna)+2],
极小值是h(0)=-2a-1;
当a=1时,函数h(x)在(-∞,+∞)上单调递增,无极值;
当a>
1时,函数h(x)在(-∞,0)和(lna,+∞)上单调递增,
在(0,lna)上单调递减,函数h(x)有极大值,也有极小值,
极大值是h(0)=-2a-1,
教师用书专用(6—17)
6.(2015福建,10,5分)若定义在R上的函数f(x)满足f(0)=-1,其导函数f'
(x)满足f'
k>
1,则下列结论中一定错误的是 ( )
A.f<
B.f>
C.f<
D.f>
7.(2013课标全国Ⅱ,10,5分)已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
A.∃x0∈R,f(x0)=0
B.函数y=f(x)的图象是中心对称图形
C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减
D.若x0是f(x)的极值点,则f'
(x0)=0
8.(2017天津,20,14分)设a∈Z,已知定义在R上的函数f(x)=2x4+3x3-3x2-6x+a在区间(1,2)内有一个零点x0,g(x)为f(x)的导函数.
(1)求g(x)的单调区间;
(2)设m∈[1,x0)∪(x0,2],函数h(x)=g(x)(m-x0)-f(m),求证:
h(m)h(x0)<
(3)求证:
存在大于0的常数A,使得对于任意的正整数p,q,且∈[1,x0)∪(x0,2],满足≥.
解析 本小题主要考查导数的运算、利用导数研究函数的性质、证明不等式等基础知识和方法.考查函数思想和化归思想.考查抽象概括能力、综合分析问题和解决问题的能力.
(1)由f(x)=2x4+3x3-3x2-6x+a,可得g(x)=f'
(x)=8x3+9x2-6x-6,进而可得g'
(x)=24x2+18x-6.令g'
(x)=0,解得x=-1或x=.
当x变化时,g'
(x),g(x)的变化情况如下表:
x
(-∞,-1)
g'
(x)
+
-
g(x)
↗
↘
所以,g(x)的单调递增区间是(-∞,-1),,单调递减区间是.
(2)证明:
由h(x)=g(x)(m-x0)-f(m),得h(m)=g(m)(m-x0)-f(m),h(x0)=g(x0)(m-x0)-f(m).
令函数H1(x)=g(x)(x-x0)-f(x),则H1'
(x)=g'
(x)(x-x0).由
(1)知,当x∈[1,2]时,g'
0,故当x∈[1,x0)时,H1'
0,H1(x)单调递减;
当x∈(x0,2]时,H1'
0,H1(x)单调递增.因此,当x∈[1,x0)∪(x0,2]时,H1(x)>
H1(x0)=-f(x0)=0,可得H1(m)>
0,即h(m)>
令函数H2(x)=g(x0)(x-x0)-f(x),则H2'
(x)=g(x0)-g(x).由
(1)知g(x)在[1,2]上单调递增,故当x∈[1,x0)时,H2'
0,H2(x)单调递增;
当x∈(x0,2]时,H2'
0,H2(x)单调递减.因此,当x∈[1,x0)∪(x0,2]时,H2(x)<
H2(x0)=0,可得H2(m)<
0,即h(x0)<
所以,h(m)h(x0)<
(3)证明:
对于任意的正整数p,q,且∈[1,x0)∪(x0,2],令m=,函数h(x)=g(x)(m-x0)-f(m).由
(2)知,当m∈[1,x0)时,h(x)在区间(m,x0)内有零点;
当m∈(x0,2]时,h(x)在区间(x0,m)内有零点.所以h(x)在(1,2)内至少有一个零点,不妨设为x1,则h(x1)=g(x1)-f=0.
由
(1)知g(x)在[1,2]上单调递增,故0<
g
(1)<
g(x1)<
g
(2),于是=≥
=.
因为当x∈[1,2]时,g(x)>
0,故f(x)在[1,2]上单调递增,所以f(x)在区间[1,2]上除x0外没有其他的零点,而≠x0,故f≠0.又因为p,q,a均为整数,所以|2p4+3p3q-3p2q2-6pq3+aq4|是正整数,从而|2p4+3p3q-3p2q2-6pq3+aq4|≥1.所以≥.所以,只要取A=g
(2),就有≥.
9.(2015广东,19,14分)设a>
1,函数f(x)=(1+x2)ex-a.
(1)求f(x)的单调区间;
f(x)在(-∞,+∞)上仅有一个零点;
(3)若曲线y=f(x)在点P处的切线与x轴平行,且在点M(m,n)处的切线与直线OP平行(O是坐标原点),证明:
m≤-1.
解析
(1)函数f(x)的定义域为R.
因为f'
(x)=2x·
ex+(1+x2)ex=(x2+2x+1)ex=(x+1)2ex≥0,
所以函数f(x)在R上单调递增,即f(x)的单调递增区间为(-∞,+∞),无单调递减区间.
因为a>
1,所以f(0)=1-a<
0,f(lna)=(1+ln2a)·
elna-a=aln2a>
所以f(0)·
f(lna)<
0,由零点存在性定理可知f(x)在(0,lna)内存在零点.
又由
(1)知,f(x)在R上单调递增,故f(x)在(-∞,+∞)上仅有一个零点.
设点P(x0,y0),由题意知,f'
(x0)=(x0+1)2=0,解得x0=-1.
所以y0=(1+)-a=-a,所以点P的坐标为.
所以kOP=a-.
由题意可得,f'
(m)=(m+1)2em=a-.
要证明m≤-1,只需要证明m+1≤,
只需要证明(m+1)3≤a-=(m+1)2em,
只需要证明m+1≤em.
构造函数:
h(x)=ex-x-1(x∈R),则h'
(x)=ex-1.
0,即h(x)在(-∞,0)上单调递减;
0,即h(x)在(0,+∞)上单调递增.
所以函数h(x)有最小值,为h(0)=0,则h(x)≥0.
所以ex-x-1≥0,故em-m-1≥0,故m+1≤em,故原不等式成立.
10.(2014课标Ⅱ,21,12分)已知函数f(x)=ex-e-x-2x.
(1)讨论f(x)的单调性;
(2)设g(x)=f(2x)-4bf(x),当x>
0时,g(x)>
0,求b的最大值;
(3)已知1.4142<
<
1.4143,估计ln2的近似值(精确到0.001).
解析
(1)f'
(x)=ex+e-x-2≥0,等号仅当x=0时成立.
所以f(x)在(-∞,+∞)上单调递增.
(2)g(x)=f(2x)-4bf(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,
(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]
=2(ex+e-x-2)(ex+e-x-2b+2).
(i)当b≤2时,g'
(x)≥0,等号仅当x=0时成立,
所以g(x)在(-∞,+∞)上单调递增.而g(0)=0,所以对任意x>
0,g(x)>
(ii)当b>
2时,若x满足2<
ex+e-x<
2b-2,即0<
x<
ln(b-1+)时,g'
0.而g(0)=0,因此当0<
x≤ln(b-1+)时,g(x)<
综上,b的最大值为2.
(3)由
(2)知,g(ln)=-2b+2(2b-1)ln2.
当b=2时,g(ln)=-4+6ln2>
ln2>
>
0.6928;
当b=+1时,ln(b-1+)=ln,
g(ln)=--2+(3+2)ln2<
ln2<
0.6934.
所以ln2的近似值为0.693.
11.(2014广东,21,14分)设函数f(x)=,其中k<
-2.
(1)求函数f(x)的定义域D(用区间表示);
(2)讨论函数f(x)在D上的单调性;
(3)若k<
-6,求D上满足条件f(x)>
f
(1)的x的集合(用区间表示).
解析
(1)由题意得(x2+2x+k)2+2(x2+2x+k)-3>
∴[(x2+2x+k)+3]·
[(x2+2x+k)-1]>
∴x2+2x+k<
-3或x2+2x+k>
1,
∴(x+1)2<
-2-k(-2-k>
0)或(x+1)2>
2-k(2-k>
0),
∴|x+1|<
或|x+1|>
∴-1-<
-1+或x<
-1-或x>
-1+,
∴函数f(x)的定义域D为
(-∞,-1-)∪(-1-,-1+)∪(-1+,+∞).
(2)f'
(x)=-
=-,
由f'
0得(x2+2x+k+1)(2x+2)<
0,即(x+1+)(x+1-)(x+1)<
∴x<
-1-或-1<
-1+,结合定义域知x<
所以函数f(x)的单调递增区间为(-∞,-1-),(-1,-1+),
同理,递减区间为(-1-,-1),(-1+,+∞).
(3)由f(x)=f
(1)得(x2+2x+k)2+2(x2+2x+k)-3=(3+k)2+2(3+k)-3,
∴[(x2+2x+k)2-(3+k)2]+2[(x2+2x+k)-(3+k)]=0,
∴(x2+2x+2k+5)·
(x2+2x-3)=0,
∴(x+1+)(x+1-)·
(x+3)(x-1)=0,
∴x=-1-或x=-1+或x=-3或x=1,
∵k<
-6,∴1∈(-1,-1+),-3∈(-1-,-1),
-1-<
-1-,-1+>
结合函数f(x)的单调性知f(x)>
f
(1)的解集为
(-1-,-1-)∪(-1-,-3)∪(1,-1+)∪(-1+,-1+).
12.(2014山东,20,13分)设函数f(x)=-k(k为常数,e=2.71828…是自然对数的底数).
(1)当k≤0时,求函数f(x)的单调区间;
(2)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
解析
(1)函数y=f(x)的定义域为(0,+∞).
f'
(x)=-k
=-=.
由k≤0可得ex-kx>
所以当x∈(0,2)时,f'
0,函数y=f(x)单调递减,
当x∈(2,+∞)时,f'
0,函数y=f(x)单调递增.
所以f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞).
(2)由
(1)知,当k≤0时,函数f(x)在(0,2)内单调递减,
故f(x)在(0,2)内不存在极值点;
当k>
0时,设函数g(x)=ex-kx,x∈[0,+∞).
因为g'
(x)=ex-k=ex-elnk,
k≤1时,
当x∈(0,2)时,g'
(x)=ex-k>
0,y=g(x)单调递增,
故f(x)在(0,2)内不存在两个极值点;
1时,
得x∈(0,lnk)时,g'
0,函数y=g(x)单调递减,
x∈(lnk,+∞)时,g'
0,函数y=g(x)单调递增.
所以函数y=g(x)的最小值为g(lnk)=k(1-lnk).
函数f(x)在(0,2)内存在两个极值点,
当且仅当解得e<
k<
.
综上所述,函数f(x)在(0,2)内存在两个极值点时,k的取值范围为.
13.(2014天津,20,14分)设f(x)=x-aex(a∈R),x∈R.已知函数y=f(x)有两个零点x1,x2,且x1<
x2.
(1)求a的取值范围;
(2)证明随着a的减小而增大;
(3)证明x1+x2随着a的减小而增大.
解析
(1)由f(x)=x-aex,
可得f'
(x)=1-aex.
下面分两种情况讨论:
①a≤0时,
0在R上恒成立,可得f(x)在R上单调递增,不合题意.
②a>
0时,由f'
(x)=0,得x=-lna.
当x变化时,f'
(x),f(x)的变化情况如下表:
(-∞,-lna)
-lna
(-lna,+∞)
f(x)
-lna-1
这时,f(x)的单调递增区间是(-∞,-lna);
单调递减区间是(-lna,+∞).
于是,“函数y=f(x)有两个零点”等价于如下条件同时成立:
(i)f(-lna)>
(ii)存在s1∈(-∞,-lna),满足f(s1)<
(iii)存在s2∈(-lna,+∞),满足f(s2)<
由f(-lna)>
0,即-lna-1>
0,解得0<
e-1.而此时,取s1=0,满足s1∈(-∞,-lna),且f(s1)=-a<
取s2=+ln,满足s2∈(-lna,+∞),且f(s2)=+<
所以a的取值范围是(0,e-1).
由f(x)=x-aex=0,有a=.设g(x)=,由g'
(x)=,知g(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减.并且,当x∈(-∞,0]时,g(x)≤0;
当x∈(0,+∞)时,g(x)>
0.由已知,x1,x2满足a=g(x1),a=g(x2).
由a∈(0,e-1),及g(x)的单调性,可得x1∈(0,1),x2∈(1,+∞).
对于任意的a1,a2∈(0,e-1),设a1>
a2,g(ξ1)=g(ξ2)=a1,其中0<
ξ1<
1<
ξ2;
g(η1)=g(η2)=a2,其中0<
η1<
η2.
因为g(x)在(0,1)上单调递增,故由a1>
a2,即g(ξ1)>
g(η1),可得ξ1>
η1;
类似可得ξ2<
η2.又由ξ1,η1>
0,得<
所以随着a的减小而增大.
由x1=a,x2=a,可得lnx1=lna+x1,lnx2=lna+x2.故x2-x1=lnx2-lnx1=ln.
设=t,则t>
1,且解得x1=,x2=.
所以x1+x2=.(*)
令h(x)=,x∈(1,+∞),则h'
(x)=.
令u(x)=-2lnx+x-,得u'
(x)=.当x∈(1,+∞)时,u'
0.因此,u(x)在(1,+∞)上单调递增,故对于任意的x∈(1,+∞),u(x)>
u
(1)=0,由此可得h'
0,故h(x)在(1,+∞)上单调递增.
因此,由(*)可得x1+x2随着t的增大而增大.
而由
(2)知t随着a的减小而增大,所以x1+x2随着a的减小而增大.
14.(2014辽宁,21,12分)已知函数f(x)=(cosx-x)(π+2x)-(sinx+1),g(x)=3(x-π)cosx-4(1+sinx)ln.
证明:
(1)存在唯一x0∈,使f(x0)=0;
(2)存在唯一x1∈,使g(x1)=0,且对
(1)中的x0,有x0+x1<
π.
证明
(1)当x∈时,f'
(x)=-(1+sinx)(π+2x)-2x-cosx<
0,函数f(x)在上为减函数,又f(0)=π->
0,f=-π2-<
0,所以存在唯一x0∈,使f(x0)=0.
(2)考虑函数h(x)=-4ln,
x∈.
令t=π-x,则x∈时,t∈.
记u(t)=h(π-t)=-4ln,
则u'
(t)=.
由
(1)得,当t∈(0,x0)时,u'
(t)>
0,当t∈时,u'
(t)<
在(0,x0)上u(t)是增函数,又u(0)=0,从而当t∈(0,x0]时,u(t)>
0,所以u(t)在(0,x0]上无零点.
在上u(t)为减函数,由u(x0)>
0,u=-4ln2<
0,知存在唯一t1∈,使u(t1)=0.
所以存在唯一的t1∈,使u(t1)=0.
因此存在唯一的x1=π-t1∈,使h(x1)=h(π-t1)=u(t1)=0.
因为当x∈时,1+sinx>
0,故g(x)=(1+sinx)h(x)与h(x)有相同的零点,所以存在唯一的x1∈,使g(x1)=0.
因x1=π-t1,t1>
x0,所以x0+x1<
15.(2014湖北,22,14分)π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)=的单调区间;
(2)求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数;
(3)将e3,3e,eπ,πe,3π,π3这6个数按从小到大的顺序排列,并证明你的结论.
解析
(1)函数f(x)的定义域为(0,+∞).
因为f(x)=,所以f'
当f'
0,即0<
e时,函数f(x)单调递增;
0,即x>
e时,函数f(x)单调递减.
故函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞).
(2)因为e<
3<
π,所以eln3<
elnπ,πlne<
πln3,即ln3e<
lnπe,lneπ<
ln3π.
于是根据函数y=lnx,y=ex,y=πx在定义域上单调递增,可得3e<
πe<
π3,e3<
eπ<
3π.
故这6个数的最大数在π3与3π之中,最小数在3e与e3之中.
由e<
π及
(1)的结论,得f(π)<
f(3)<
f(e),
即<
由<
得lnπ3<
ln3π,所以3π>
π3;
得ln3e<
lne3,所以3e<
e3.
综上,6个数中的最大数是3π,最小数是3e.
(3)由
(2)知,3e<
π3<
3π,3e<
又由
(2)知,<
得πe<
eπ.
故只需比较e3与πe和eπ与π3的大小.
由
(1)知,当0<
e时,f(x)<
f(e)=,即<
在上式中,令x=,又<
e,则ln<
从而2-lnπ<
即得lnπ>
2-