冲刺NOIP模拟试题与解析一Word下载.docx
《冲刺NOIP模拟试题与解析一Word下载.docx》由会员分享,可在线阅读,更多相关《冲刺NOIP模拟试题与解析一Word下载.docx(15页珍藏版)》请在冰豆网上搜索。
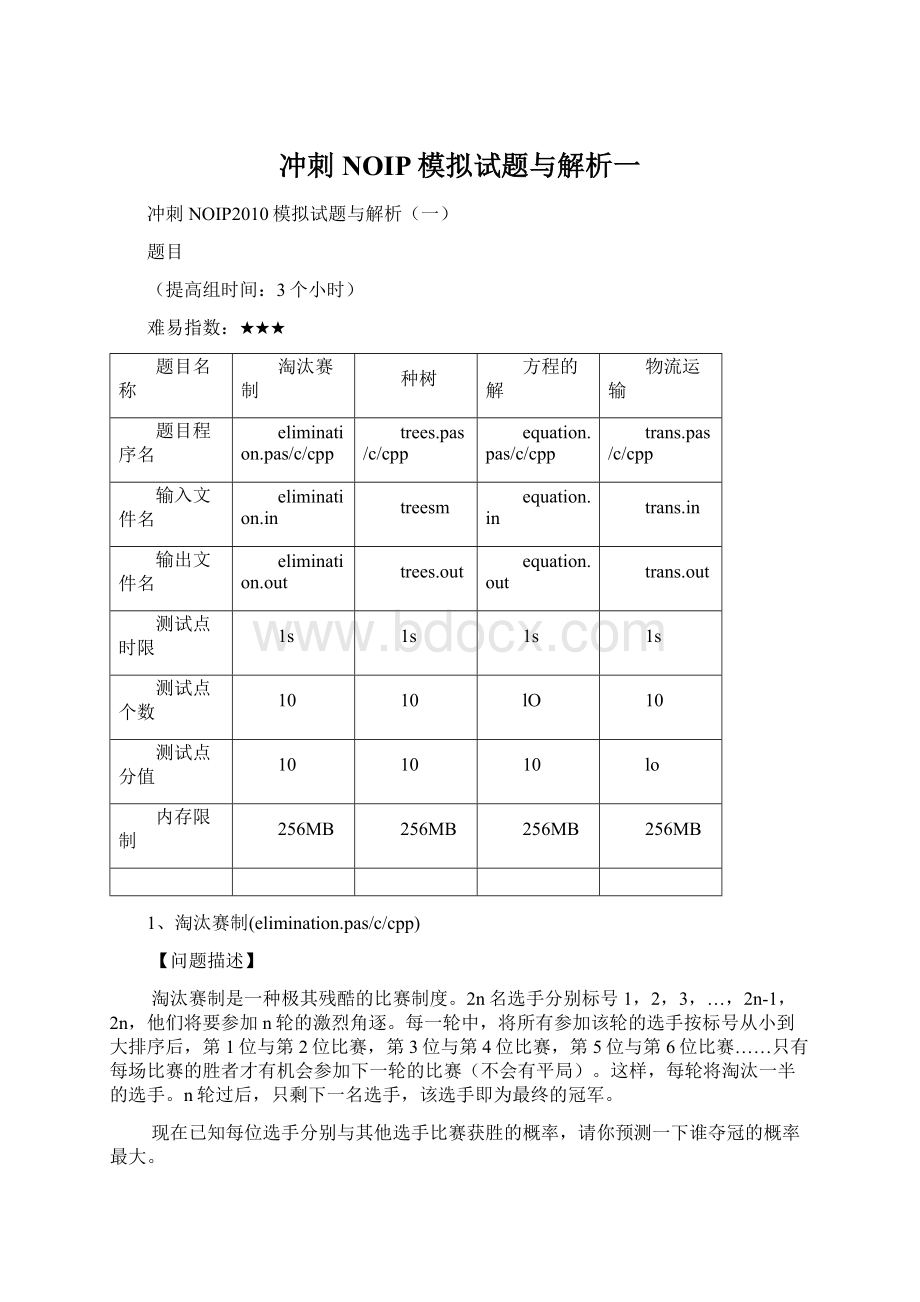
接下来2n行,每行2n个整数,第i行第j个是pij(0≤pij≤100,pii=0,pij+pji=100),表示第i号选手与第j号选手比赛获胜的概率。
【输出文件】
输出文件elimination.out。
只有一个整数c,表示夺冠概率最大的选手编号(若有多位选手,输出编号最小者)。
【样例输入】
2
0905050
1001010
5090050
5090500
【样例输出】
1
【数据规模】
30%的数据满足n≤3;
100%的数据满足n≤10。
2、种树(trees.pas/c/cpp)
一条街的一边有几座房子。
因为环保原因居民想要在路边种些树。
路边的地区被分割成块,并被编号为l…n。
每个块的大小为一个单位尺寸并最多可种一棵树。
每个居民想在门前种些树并指定了三个号码b,e,t。
这三个数表示该居民想在b和e之间最少种t棵树。
当然,b≤e,居民必须保证在指定地区不能种多于地区被分割成块数的树,即要求t≤e-b+1,允许居民想种树的各自区域可以交叉。
出于资金短缺的原因,环保部门请你求出能够满足所有居民的要求,需要种树的最少数量。
【文件输入】
第一行为n,表示区域的个数;
第二行为h,表示房子的数目;
下面h行描述居民的需要:
bet(0<
b≤e≤30000,r≤e-b+l)分别用一个空格分开。
【文件输出】
输出为满足所有要求的最少树的数量。
【样饲输入】
9
4
142
462
892
352
【样例输出】
5
【数据规模】
30%的数据满足0<
n≤1000,0<
h≤500;
100%的数据满足n≤30000,h≤5000。
3、方程的解(equation.pas/c/cpp)
佳佳碰到了一个难题,请你来帮忙解决。
对于不定方程a1+a2+…+ak-1+ak=g(x),其中k≥2且k∈N,x是正整数,g(x)=xxmod1000(即xx除以1000的余数),x,k是给定的数。
我们要求的是这个不定方程的正整数解组数。
举例来说,当k=3,x=2时,分别为(a1,a2,a3)=(2,1,1)'
(1,2,1),(1,1,2)。
输入文件equation.in有且只有一行,为用空格隔开的两个正整数,依次为k,x。
【文件输出】
输出文件equation.out有且只有一行,为方程的正整数解组数。
【样例输入】
32
3
【数据范围】
对于40%的数据,ans≤1016;
对于100%的数据,k≤100,x≤231-1,k≤g(x)。
4、物流运输(trans.pas/c/cpp)
物流公司要把一批货物从码头A运到码头B。
由于货物量比较大,需要n天才能运完。
货物运输过程中一般要转停好几个码头。
物流公司通常会设计一条固定的运输路线,以便对整个运输过程实施严格的管理和跟踪。
由于各种因素的存在,有的时候某个码头会无法装卸货物。
这时候就必须修改运输路线,让货物能够按时到达目的地。
但是修改路线是—件十分麻烦的事情,会带来额外的成本。
因此物流公司希望能够订一个n天的运输计划,使得总成本尽可能地小。
第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。
n表示货物运输所需天数,m表示码头总数,K表示每次修改运输路线所需成本。
接下来e行每行是一条航线描述,包括了三个整数,依次表示航线连接的两个码头编号以及航线长度(>
0)。
其中码头A编号为1,码头B编号为m。
单位长度的运输费用为1。
航线是双向的。
再接下来一行是一个整数d,后面的d行每行是三个整数P(1<
P<
m),a,b(1≤a≤b≤n)。
表示编号为P的码头从第a天到第b天无法装卸货物(含头尾)。
同一个码头有可能在多个时间段内不可用。
但任何时间都存在至少一条从码头A到码头B的运输路线。
包括了一个整数表示最小的总成本。
总成本=n天运输路线长度之和+K*改变运输路线的次数。
55108
121
133
142
232
244
341
352
452
4
223
311
333
445
32
【样例输入说明】
上图依次表示第1至第5天的情况,阴影表示不可用的码头。
【样例输出说明】
前三天走1-4-5,后两天走1-3-5,这样总成本为(2+2)*3+(3+2)*2+10=32。
解题报告
1、淘汰赛制
【方法一】动态规划
设d[i,j]表示第j位选手通过第i轮的概率;
P[i,j]表示第i号选手与第j号选手比赛获胜的概率;
状态转移方程:
d[i,j]=d[i-l,j]*sum{d[i-l,k]*p[j,k]}(i=l..n,j=1..2n,k为所有可能在第i轮与第j位选手交战的选手编号),边界条件d[0,j]=1。
时间复杂度O(n2*2n)。
【参考程序】
【方法二】分治
#include<
iostream>
usingnamespacestd;
doublef[12][1206]={0),a[1026][1026];
intn;
voiddfs(int1,intr,intk)//分治处理
{
if(k==0)return;
inti,j,mid=(l+r)/2;
dfs(1,mid,k-l);
dfs(mid+l,r,k-l);
for(i=l;
i<
=mid;
i++)
for(j=mid+l;
j<
=r;
j++)
{
f[k][i]+=f[k-1][i]*f[k-l][j]*a[i][j];
f[k][j]+=f[k-1][i]*f[k-1][j]*a[j][i];
}
}
intmain()
inti,j,k,p;
cin>
>
n;
p=1<
<
for(i=1;
i<
=p;
i++)
for(j=1;
j<
j++)
doublec;
intq;
scanf("
%d"
&
q);
c=q;
a[i][j]=double(c/100);
for(i=1;
i++)f[0][i]=1;
dfs(1,p,n);
k=0;
i++)//寻找最大的概率
cout<
k;
return0;
2、种树
【方法一】贪心
题目中要求要种树种得少,就要使一棵树给多个区间使用,这样,尽量在重叠区间种树即可,而重叠位置一定是区间尾部。
处理问题时,先按所有区间的结束位置排序,若结束位置相同,则按开始位置从大到小排序。
之后依次处理每个区间,先在第一个区间尾部种满足要求的树,对下一个区间,看差多少棵就在该区间尾部种多少。
【算法步骤】
1、先快排
2、对每个区间依次处理
a、从前到后扫描这个区间,统计点的个数;
b、若点的个数超过了要求的点数,则continue,
c、从该区间后向前扫描,添加覆盖点。
3、输出ans
【参考程序】
#include<
structline{ints,e,v;
}a[5005],mid;
intn,m;
boolused[30005]={0};
voidqsort(intl,intr)//快排
{inti=l,j=r,
mid=a[(l+r)/2];
while(i<
=j)
{
while(a[i].e<
mid.e||(a[i].e==mid.e&
&
a[i].s>
mid.s))i++;
while(a[j].e>
mid.e||(a[j].e==mid.e&
a[j].s<
mid.s))j--;
if(i<
=j)swap(a[i++],a[j--]);
if(l<
j)qsort(1,j);
if(i<
r)qsort(i,r);
voidinit()
{inti;
cin>
n>
m;
=m;
i++)cin>
a[i].e>
a[i].v;
qsort(1,m);
voidsolve()
{inti,j,k,ans=0;
i++)
for(j=a[i].s;
=a[i].e;
if(used[j])k++;
if(k>
=a[i].v)continue;
for(j=a[i].e;
j>
=a[i].s;
j--)
if(!
used[j])
{used[j]=l;
k++;
if(k==a[i].v)break;
ans;
}.
init();
solve();
return0;
【方法二】差分约束系统
constintoo=0x7fffffff/2;
struct{intto,v,next;
}w[3000005];
intdis[30005],N,n=0,q[3000005],cnt=0,h[30005]={0};
boolr[30005l={0};
voidaddedge(intx,inty,intz)
{
cnt++;
if(x==0)x=n+1;
if(y==0)y=n+1;
w[cnt].to=y;
w[cnt].v=z,w[cnt].next=h[x];
h[x]=cnt;
voidInit()
{intx,y,z,e,i;
e;
while(e--)
scanf(“%d%d%d”,&
x,&
y,&
z);
addedge(y,x-1,-z);
=n;
{addedge(i-l,i,1);
addedge(i,i-l,0);
voidspfa()
inti,t,p,1=1,r=l,
for(i=l;
=n+l;
i++)dis[i]=oo;
q[1]=n;
f[n]=1;
dis[n]=0;
while(l<
=r)
while(p!
=0)
if(dis[t]+w[p].v<
dis[w[p].to])
dis[w[p].to]=dis[t]+w[p].v;
if(!
f[w[p].to]){q[++r]=w[p].to;
f[w[p].to]=1;
p=w[p].next;
l++;
f[t]=0;
cout<
abs(dis[n+l]);
Init0,
spfa();
3、方程的解
【题目考点】分治+组合数学+高精
【题目分析】
其实这个题目,可能很多牛一看就知道怎么做。
我们令n=g(x),则答案即为C(n-l,k-l)。
关于高精度求组合数,我的解法没有用除法,否则太麻烦,可以按照组合数公式逐个把分母的数约分掉,然后按剩下的分子乘起来即可,具体请看程序代码。
剩下的任务是如何求g(x),就是二分快速幂的方法。
constintone=10000,
intk,x,ans[l000]={0},p[2000]={0};
intt,c[100]={0},i;
k>
x;
t=x,
x%=1000;
while(t>
0){c[++c[0]]=t%2;
t/=2;
t=x;
for(i=c[0]-1;
i>
=1;
i--)
{x=x*x%l000;
if(c[i]==1)x=x*t%1000;
voidPrint(inta[])
if(a[0]==0){cout<
0;
return;
inti,j;
a[a[0]];
for(i=a[0]-1;
1>
1--)
for(j=one/10;
=l,j/=10)cout<
a[i]/j%10;
voidadd(intx,intd)
inti;
while(x%i==0){x/=i;
p[i]+=d;
if(x>
1)p[x]+=d;
voidMul(inta[],intw)
=a[0];
i++)a[i]*=w;
{a[i+1]+=a[i]/one;
a[i]%=one;
while(a[a[0]+1]>
0)
{a[0]++;
a[a[0]+l]+=a[a[0]]/one,
a[a[0]]%=one;
voidC(intm,intn)
inti,j;
if(m>
n||n==0){cout<
if(m==0||m==n){cout<
1;
i++){add(n-m+i,l);
add(i,-1);
ans[0]=ans[1]=1;
=1000;
for(j=l;
=p[i];
j++)Mul(ans,i);
Print(ans);
Init(),
C(k-l,x-l);
4、物流运输
【题目考点】单源最短路+dp。
【题目分析】
f[i]=min{a(1,i)*i,f[j]+a(j+1,i)*(i-j)+k)(1=<
j≤i-1)。
f[i]表示前i天的最小运费,a(x,y)表示从第x天到第y天从起点到终点的最短路,可以用bellmanford,dijkstra,SPFA……方程很好理解。
第一种情况:
1到j天都走一条路。
第二种情况:
j+l到i天走一条路(这条路记为路径1)。
这个时候,不管前j天走的路径。
constirrtoo=0x7fffff/2;
intm,n,k,a[105][105],map[25][25]={0};
intw[105][105]={0},dis[25],f[105]={0};
boolbad[25],v[25];
voidInit()
{
intx,y,z,e,i;
m>
while(e--)
x>
y>
z;
map[x][y]=map[y][x]=z;
e,
for(i=y;
=z;
i++)w[i][++w[i][0]]=x;
//w[i][w[i][0]]表示第i天d[i]个码头为x;
//w[i][0]表示第i天不能用的码头数;
}
iritdijkstra()
{inti,j,k,Min;
i++)dis[i]=oo,v[i]=0;
dis[1]=0;
Min=oo;
v[j]&
!
bad[j]&
dis[j]<
Min)Min=dis[j],k=j;
if(k==0)break;
v[k]=true;
if(map[k][j]>
0&
dis[k]+map[k][j]<
dis[j])dis[j]=map[k][j]+dis[k];
returndis[n];
voidPre()//用dijkstra来初始化
{inti,j,k,t;
for(j=i;
memset(bad,0,sizeof(bad));
for(k=i;
k<
=j;
k++)
for(t=1;
t<
w[k][0];
t++)bad[w[k][t]]=true,
a[i][j]=dijkstra();
voidDP()//动态规划求解
{inti,j;
f[i]=oo;
for(j=0;
i;
if(f[j]+a[j+1][i]*(i-j)+k<
f[i])f[i]=f[j]+a[j+1][i]*(i-j)+k;
f[m]-K;
Init();
Pre();
DP();