23 变量的相关性Word文档格式.docx
《23 变量的相关性Word文档格式.docx》由会员分享,可在线阅读,更多相关《23 变量的相关性Word文档格式.docx(16页珍藏版)》请在冰豆网上搜索。
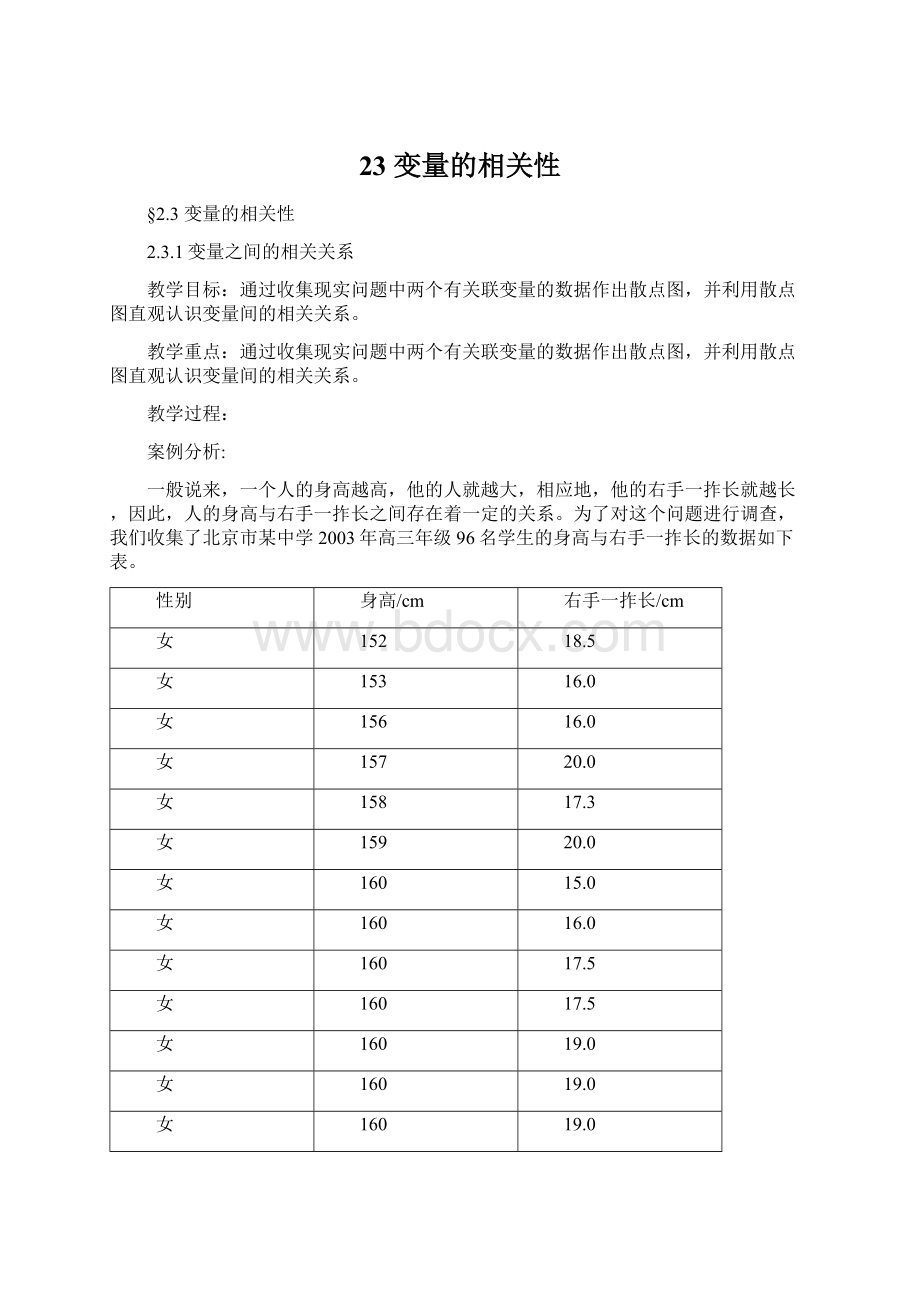
164
17.0
165
166
167
168
170
21.0
171
172
173
22.0
男
169
22.3
23.0
174
175
21.2
176
177
178
22.5
24.0
179
180
181
21.1
182
183
185
25.0
186
191
(1)根据上表中的数据,制成散点图。
你能从散点图中发现身高与右手一拃长之间的近似
关系吗?
(2)如果近似成线性关系,请画出一条直线来近似地表示这种线性关系。
(3)如果一个学生的身高是188cm,你能估计他的一拃大概有多长吗?
解:
根据上表中的数据,制成的散点图如下。
从散点图上可以发现,身高与右手一拃长之间的总体趋势是成一直线,也就是说,它们之间是线性相关的。
那么,怎样确定这条直线呢?
同学1:
选择能反映直线变化的两个点,例如(153,16),(191,23)二点确定一条直线。
同学2:
在图中放上一根细绳,使得上面和下面点的个数相同或基本相同。
同学3:
多取几组点对,确定几条直线方程。
再分别算出各个直线方程斜率、截距的算术平均值,作为所求直线的斜率、截距。
同学4:
我从左端点开始,取两条直线,如下图。
再取这两条直线的“中间位置”作一条直线。
同学5:
我先求出相同身高同学右手一拃长的平均值,画出散点图,如下图,再画出近似的直线,使得在直线两侧的点数尽可能一样多。
同学6:
我先将所有的点分成两部分,一部分是身高在170cm以下的,一部分是身高在170cm以上的;
然后,每部分的点求一个“平均点”——身高的平均值作为平均身高、右手一拃的平均值作为平均右手一拃长,即(164,19),(177,21);
最后,将这两点连接成一条直线。
同学7:
我先将所有的点按从小到大的顺序进行排列,尽可能地平均分成三等份;
每部分的点按照同学3的方法求一个“平均点”,最小的点为(161.3,18.2),中间的点为(170.5,20.1),最大的点为(179.2,21.3)。
求出这三个点的“平均点”为(170.3,19.9)。
我再用直尺连接最大点与最小点,然后平行地推,画出过点(170.3,19.9)的直线。
同学8:
取一条直线,使得在它附近的点比较多。
在这里需要强调的是,身高和右手一拃长之间没有函数关系。
我们得到的直线方程,只是对其变化趋势的一个近似描述。
对一个给定身高的人,人们可以用这个方程来估计这个人的右手一拃长。
这是十分有意义的。
课堂练习:
第77页,练习A,练习B
小结:
课后作业:
第84页,习题2-3A第1
(1)、2
(1)题,
2.3.2两个变量的线性相关
经历用不同估算方法描述两个变量线性相关的过程。
知道最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程。
1.回顾上节课的案例分析给出如下概念:
(1)回归直线方程
(2)回归系数
2.最小二乘法
3.直线回归方程的应用
(1)描述两变量之间的依存关系;
利用直线回归方程即可定量描述两个变量间依存的数量关系
(2)利用回归方程进行预测;
把预报因子(即自变量x)代入回归方程对预报量(即因变量Y)进行估计,即可得到个体Y值的容许区间。
(3)利用回归方程进行统计控制规定Y值的变化,通过控制x的范围来实现统计控制的目标。
如已经得到了空气中NO2的浓度和汽车流量间的回归方程,即可通过控制汽车流量来控制空气中NO2的浓度。
4.应用直线回归的注意事项
(1)做回归分析要有实际意义;
(2)回归分析前,最好先作出散点图;
(3)回归直线不要外延。
5.实例分析:
某调查者从调查中获知某公司近年来科研费用支出(
)与公司所获得利润(
)的统计资料如下表:
科研费用支出(
)与利润(
)统计表单位:
万元
年份
科研费用支出
利润
1998
1999
2000
2001
2002
2003
5
11
4
3
2
31
40
30
34
25
20
合计
要求估计利润(
)对科研费用支出(
)的线性回归模型。
设线性回归模型直线方程为:
因为:
根据资料列表计算如下表:
155
440
120
75
121
16
9
6
-1
-2
-3
1
10
-5
-10
36
60
1000
200
50
100
现利用公式(Ⅰ)、(Ⅱ)、(Ⅲ)求解参数
的估计值:
所以:
利润(
)的线性回归模型直线方程为:
6、求直线回归方程,相关系数和作图,这些EXCEL可以方便地做到。
仍以上题的数据为例。
于EXCEL表中的空白区,选用"
插入"
菜单命令中的"
图表"
,选中XY散点图类型,在弹出的图表向导中按向导的要求一步一步地操作,如有错误可以返回去重来或在以后修改。
适当修饰图的大小、纵横比例、字体大小、和图符的大小等,使图美观,最后得到图1,图中有直线称为趋势线,还有直线方程和相关系数。
图中的每一个部份如坐标、标题、图例等都可以分别修饰,这里主要介绍趋势线和直线方程。
图1散点图
鼠标右键点击图中的数据点,出现一个对话框,选"
添加趋势线"
,图中自动画上一条直线,再以鼠标右击此线,出现趋势线格式对话框,选择线条的粗细和颜色,在选项中选取显示公式和显示R平方值,确定后即在图中显示回归方程和相关系数。
第83页,练习A,练习B
第84页,习题2-3A第1、2题,
2.3.3实习作业
会用随机抽样的基本方法和样本估计总体的思想,解决一些简单的实际问题;
能通过对数据的分析为合理的决策提供一些依据,认识统计的作用,体会统计思维与确定性思维的差异。
1.课本86页案例设计一个题目
2.尝试解决下面的问题。
(1)下面是关于吸烟情况的20个国家的统计数字,其中第一行是国名,第二行是男性吸烟成员的百分数,第三行是女性吸烟成员的百分数。
韩国
拉脱
维亚
俄罗斯
多米
尼加
汤加
土耳其
中国
泰国
斐济
日本
68.2
67.0
66.3
65.0
63.0
61.0
60.0
59.3
59.0
6.3
12.0
30.0
13.6
14.0
7.0
30.6
14.8
美国
巴基
斯坦
芬兰
土库曼
尼日
利亚
巴拉圭
巴林
新西兰
瑞典
巴哈马
28.1
27.4
27.0
26.6
24.4
24.1
19.3
23.5
4.4
1.5
6.7
5.5
6.0
3.8
根据以上数据,试研究这些国家吸烟状况的类似程度。
问题
(1)的分析:
要根据数据研究这些国家吸烟状况的类似程度,我们可以仅讨论男性的吸烟情况,首先确定一个划分类似的标准,不妨取1%,即当两个国家男性吸烟人数百分比之差小于1%时,将这两个国家称为类似的.则可分成下面九组:
(1)韩国;
(2)拉脱维亚,俄罗斯和多米尼加;
(3)汤加;
(4)土耳其;
(5)中国,泰国,斐济和日本;
(6)美国;
(7)巴基斯坦,芬兰和土库曼;
(8)尼日利亚,巴拉圭,巴林和新西兰;
(9)瑞典和巴哈马。
对于女性吸烟的情况也可做类似的分析。
如果我们要整体地讨论吸烟情况,我们应当怎样做呢?
一个直接的想法就是考虑下面的平面图:
以女性吸烟者的百分数为横轴,男性吸烟者的百分数为纵轴。
(如下图所示)
从图中可以看出,基本上分成下面四组:
(1)巴哈马,巴基斯坦,巴拉圭,巴林,尼日利亚和土库曼斯坦;
(2)芬兰,新西兰,瑞典和美国;
(3)中国,日本,泰国,韩国,拉脱维亚,多米尼加和汤加;
(4)土耳其,斐济和俄罗斯。
这个过程叫做聚类分析,它的基本思想是:
在一批样本数据中,定义能度量样本数据或类别间相近程度的统计量,在此基础上计算出个样本数据或类别之间的相近程度度量值;
再按相近程度的大小,把样本逐一归类,关系密切的聚集到一个小的分类单位,关系疏远的聚集到一个大的分类单位,直到所有的样本数据都聚集完毕;
最后把不同的类别一一划分出来,形成一个关系密疏图,并用以直观地显示分类对象的差异和联系。
上例向我们展示了对数据进行的聚类分析的过程,一般来说,进行聚类分析需要解决两个问题:
一是如何确定度量两个数据的接近程度的方法;
二是究竟分成多少类合适。
这两个问题都需要根据实际问题的背景和数据本身的意义来确定。
统计上对此提出了一套程序化的方法:
(1)选择一种确定接近程度的方法,最直接的就是点之间的距离,我们上面的分析即是基于此;
(不同的方法将得到不同的分类结果)
(2)设要分类的对象有n个;
我们以这n个对象分成n类开始,按所选择的方法确定这n个对象两两的接近程度度量值,将最接近的两个对象合并为一类,如此我们得到了至多n-1类;
(3)确定类与类之间接近程度的方法;
(4)对n-1类重复步骤
(2),如此下去到完全归为一类止。
至于究竟分成多少类合适,需要分析者根据所讨论的问题来决定。
在实际问题中,往往需要对几种分类方案进行比较后,再加以选择。
(2)为了研究某种新药的副作用(如恶心等),给50位患者服用此新药,另外50位患者服用安慰剂,得到下列实验数据:
副作用
药物
有
无
新药
15
35
安慰剂
46
19
81
请问服用新药是否可产生副作用?
问题
(2)的分析:
假定服用新药与产生副作用没有关联.那么,首先要给“没有关联”下一个“能够操作”的定义。
根据直观的经验,在服用新药与产生副作用的情形下,这个定义可以是这样的:
如果服用新药与产生副作用没有关联,就意味着,无论服用新药与否,产生副作用的概率都是一样的。
就此例题而言:
二者相差较大。
由此可以推断,开始的假设是不成立的。
也就是说,服用新药与产生副作用是有关联的。
由统计的常识知道,要求等号成立是非常苛刻的条件,实际上一般也是办不到的,我们所能追求的是在概率意义下的可靠性。
对于上面的独立性问题,类比在聚类分析讨论中的想法,我们应当寻找一个适当的统计量,用它的大小来说明独立性是否成立。
在统计中,我们引入下面的量
副作用B
药物A
有副作用B1
无副作用B2
新药A1
安慰剂A2
在前面的例子中
a=15,b=35,c=4,d=46。
注意到独立性要求:
P(全体生实验者产生副作用)=P(服用新药产生副作用)
即
这等价于
因此,可以用
的大小来衡量独立性的好坏。
问题:
(1)用
+
是不是更好些?
(2)用
比用
合理,你认为有道理吗?
(3)为了得到统计量的近似的分布,统计学家最终选用了:
Q2=
用它的大小来衡量独立性的大小,你能把它化简得到下式吗?
从上面的表达式可以直观地看出:
的值越小,事件A与B之间的独立性将会越大(当
的值为0时,事件A与B完全独立)。
通过有关统计量分布的计算可知:
当
时,事件A与B在概率为95%的意义下是相关的;
时,事件A与B在概率为99%的意义下是相关的。
我们来算一算本题中
的值:
于是得出结论:
在概率为99%的意义下,服用新药与产生副作用是相关联的。
从数据可以进一步看出,服用新药更容易产生副作用。
上述过程在统计推断叫做独立性检验,它的基本思想是:
如何选用一个标准,用它来衡量事件之间的独立性是否成立。
在独立性检验中,我们要特别关注方法的直观及合理性。