《现代控制理论》课后习题全部答案(最完整打印版)资料下载.pdf

《现代控制理论》课后习题全部答案(最完整打印版)资料下载.pdf

《《现代控制理论》课后习题全部答案(最完整打印版)资料下载.pdf》由会员分享，可在线阅读，更多相关《《现代控制理论》课后习题全部答案(最完整打印版)资料下载.pdf（48页珍藏版）》请在冰豆网上搜索。

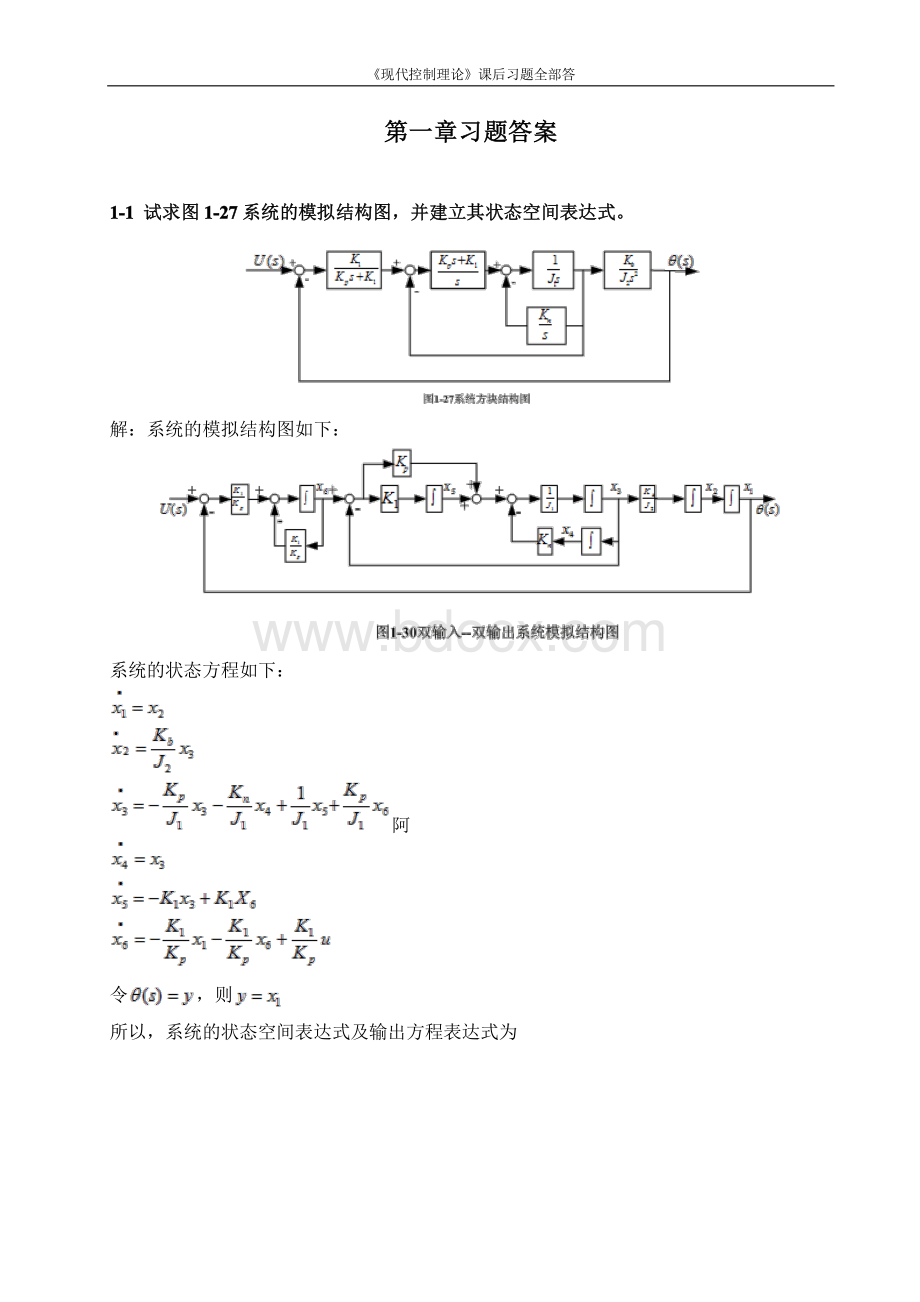
现代控制理论课后习题全部答11-33参参考考例例子子11-33（PP1199）.11-44两两输输入入，两两输输出出，的的系系统统，其其模模拟拟结结构构图图如如图图11-3300所所示示，试试求求其其状状态态空空间间表表达达式式和和传传递递函函数数阵阵。

系统的状态空间表达式如下所示：

现代控制理论课后习题全部答11-55系系统统的的动动态态特特性性由由下下列列微微分分方方程程描描述述列写其相应的状态空间表达式，并画出相应的模拟结构图。

令，则有相应的模拟结构图如下：

11-66（22）已已知知系系统统传传递递函函数数,试试求求出出系系统统的的约约旦旦标标准准型型的的实实现现，并并画画出出相相应应的的模模拟拟结结构构图图解：

现代控制理论课后习题全部答11-77给给定定下下列列状状态态空空间间表表达达式式

（1）画出其模拟结构图

（2）求系统的传递函数解：

（2）现代控制理论课后习题全部答11-88求求下下列列矩矩阵阵的的特特征征矢矢量量（3）解：

A的特征方程解之得：

当时，解得：

令得（或令，得）当时，解得：

令得11-99将将下下列列状状态态空空间间表表达达式式化化成成约约旦旦标标准准型型（并并联联分分解解）现代控制理论课后习题全部答

（2）解：

A的特征方程当时，解之得令得当时，解之得令得当时，解之得令得现代控制理论课后习题全部答约旦标准型11-1100已已知知两两系系统统的的传传递递函函数数分分别别为为WW11（ss）和和WW22（ss）试试求求两两子子系系统统串串联联联联结结和和并并联联连连接接时时，系系统统的的传传递递函函数数阵阵，并并讨讨论论所所得得结结果果解：

（1）串联联结

（2）并联联结11-1111（第第33版版教教材材）已已知知如如图图11-2222所所示示的的系系统统，其其中中子子系系统统11、22的的传传递递函函数数阵阵分分别别为为求系统的闭环传递函数解：

现代控制理论课后习题全部答11-1111（第第22版版教教材材）已已知知如如图图11-2222所所示示的的系系统统，其其中中子子系系统统11、22的的传传递递函函数数阵阵分分别别为为求求系系统统的的闭闭环环传传递递函函数数解：

现代控制理论课后习题全部答11-1122已已知知差差分分方方程程为为试试将将其其用用离离散散状状态态空空间间表表达达式式表表示示，并并使使驱驱动动函函数数uu的的系系数数bb（即即控控制制列列阵阵）为为（11）解法1：

解法2：

求T,使得得所以现代控制理论课后习题全部答所以，状态空间表达式为现代控制理论课后习题全部答第第二二章章习习题题答答案案现代控制理论课后习题全部答现代控制理论课后习题全部答现代控制理论课后习题全部答22-44用用三三种种方方法法计计算算以以下下矩矩阵阵指指数数函函数数。

（2）A=解：

第一种方法：

令则，即。

求解得到，当时，特征矢量由，得即，可令现代控制理论课后习题全部答当时，特征矢量由，得即，可令则，第二种方法，即拉氏反变换法：

第三种方法，即凯莱哈密顿定理由第一种方法可知，现代控制理论课后习题全部答22-55下下列列矩矩阵阵是是否否满满足足状状态态转转移移矩矩阵阵的的条条件件，如如果果满满足足，试试求求与与之之对对应应的的AA阵阵。

（33）（44）解：

（3）因为，所以该矩阵满足状态转移矩阵的条件（4）因为，所以该矩阵满足状态转移矩阵的条件22-66求求下下列列状状态态空空间间表表达达式式的的解解：

初始状态，输入时单位阶跃函数。

现代控制理论课后习题全部答因为，现代控制理论课后习题全部答现代控制理论课后习题全部答22-99有有系系统统如如图图22.22所所示示，试试求求离离散散化化的的状状态态空空间间表表达达式式。

设设采采样样周周期期分分别别为为TT=00.11ss和和11ss，而而和和为为分分段段常常数数。

图2.2系统结构图解：

将此图化成模拟结构图列出状态方程现代控制理论课后习题全部答则离散时间状态空间表达式为由和得：

当T=1时当T=0.1时现代控制理论课后习题全部答现代控制理论课后习题全部答现代控制理论课后习题全部答现代控制理论课后习题全部答第第三三章章习习题题答答案案33-11判判断断下下列列系系统统的的状状态态能能控控性性和和能能观观测测性性。

系系统统中中aa,bb,cc,dd的的取取值值对对能能控控性性和和能能观观性性是是否否有有关关，若若有有关关，其其取取值值条条件件如如何何？

（1）系统如图3.16所示：

由图可得：

状态空间表达式为：

由于、与无关，因而状态不能完全能控，为不能控系统。

由于只与有关，因而系统为不完全能观的，为不能观系统。

（3）系统如下式：

现代控制理论课后习题全部答解：

如状态方程与输出方程所示，A为约旦标准形。

要使系统能控，控制矩阵b中相对于约旦块的最后一行元素不能为0，故有。

要使系统能观，则C中对应于约旦块的第一列元素不全为0，故有。

33-22时时不不变变系系统统试试用用两两种种方方法法判判别别其其能能控控性性和和能能观观性性。

方法一：

方法二：

将系统化为约旦标准形。

现代控制理论课后习题全部答，中有全为零的行，系统不可控。

中没有全为0的列，系统可观。

33-33确确定定使使下下列列系系统统为为状状态态完完全全能能控控和和状状态态完完全全能能观观的的待待定定常常数数解：

构造能控阵：

要使系统完全能控，则，即构造能观阵：

要使系统完全能观，则，即33-44设设系系统统的的传传递递函函数数是是

（1）当a取何值时，系统将是不完全能控或不完全能观的？

现代控制理论课后习题全部答

（2）当a取上述值时，求使系统的完全能控的状态空间表达式。

（3）当a取上述值时，求使系统的完全能观的状态空间表达式。

（1）方法1：

系统能控且能观的条件为W（s）没有零极点对消。

因此当a=1,或a=3或a=6时，系统为不能控或不能观。

方法2：

系统能控且能观的条件为矩阵C不存在全为0的列。

（2）当a=1,a=3或a=6时，系统可化为能控标准I型（3）根据对偶原理，当a=1,a=2或a=4时，系统的能观标准II型为33-66已已知知系系统统的的微微分分方方程程为为：

试试写写出出其其对对偶偶系系统统的的状状态态空空间间表表达达式式及及其其传传递递函函数数。

系统的状态空间表达式为现代控制理论课后习题全部答传递函数为其对偶系统的状态空间表达式为：

传递函数为33-99已已知知系系统统的的传传递递函函数数为为试试求求其其能能控控标标准准型型和和能能观观标标准准型型。

系统的能控标准I型为现代控制理论课后习题全部答能观标准II型为33-1100给给定定下下列列状状态态空空间间方方程程，试试判判别别其其是是否否变变换换为为能能控控和和能能观观标标准准型型。

33-1111试试将将下下列列系系统统按按能能控控性性进进行行分分解解（11）解：

rankM=23，系统不是完全能控的。

构造奇异变换阵：

，其中是任意的，只要满足满秩。

现代控制理论课后习题全部答即得33-1122试试将将下下列列系系统统按按能能观观性性进进行行结结构构分分解解

（1）解：

由已知得则有rankN=23，该系统不能观构造非奇异变换矩阵，有则33-1133试试将将下下列列系系统统按按能能控控性性和和能能观观性性进进行行结结构构分分解解

（1）解：

由已知得现代控制理论课后习题全部答rankM=3，则系统能控rankN=3，则系统能观所以此系统为能控并且能观系统取，则则，33-1144求求下下列列传传递递函函数数阵阵的的最最小小实实现现。

（1）解：

，系统能控不能观取，则所以，所以最小实现为，验证：

现代控制理论课后习题全部答33-1155设设和和是是两两个个能能控控且且能能观观的的系系统统

（1）试分析由和所组成的串联系统的能控性和能观性，并写出其传递函数；

（2）试分析由和所组成的并联系统的能控性和能观性，并写出其传递函数。

（1）和串联当的输出是的输入时，则rankM=23，所以系统不完全能控。

当得输出是的输入时，因为rankM=3则系统能控因为rankN=20）。

因为满秩，系统能观，可构造观测器。

系统特征多项式为，所以有于是现代控制理论课后习题全部答引入反馈阵，使得观测器特征多项式：

根据期望极点得期望特征式：

比较与各项系数得：

即，反变换到x状态下观测器方程为：

现代控制理论课后习题全部答5-13类似于5-12，设计略。