完整word版八年级数学培优综合训练题.docx

完整word版八年级数学培优综合训练题.docx

《完整word版八年级数学培优综合训练题.docx》由会员分享，可在线阅读，更多相关《完整word版八年级数学培优综合训练题.docx（11页珍藏版）》请在冰豆网上搜索。

完整word版八年级数学培优综合训练题

2014-2015学年度第一学期八年级数学期末复习试题精选

一，《三角形》部分；

1，已知，在四边形ABCD中．∠A=∠C=90゜．

（1）求证：

∠ABC+∠ADC=180゜；

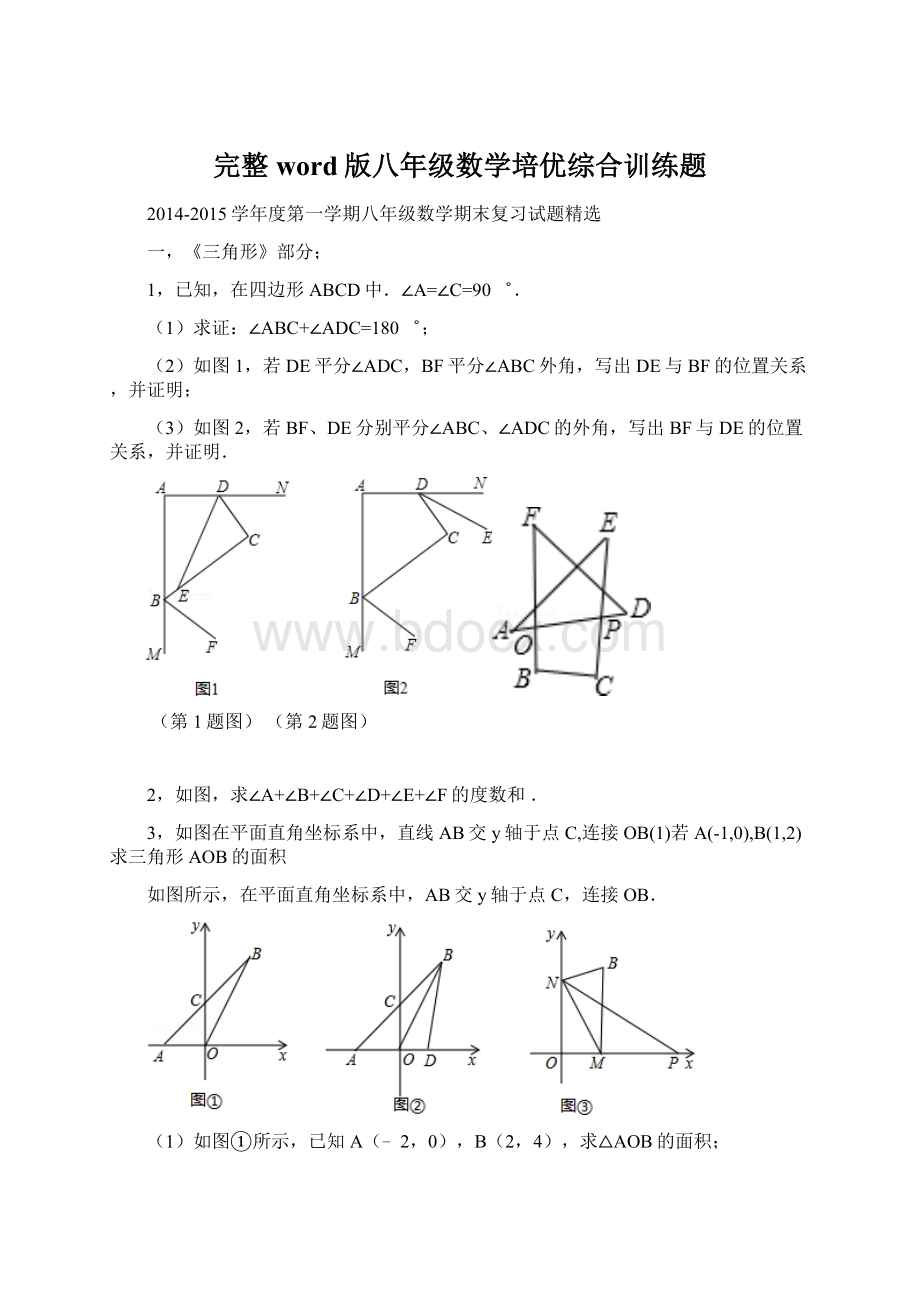
（2）如图1，若DE平分∠ADC，BF平分∠ABC外角，写出DE与BF的位置关系，并证明；

（3）如图2，若BF、DE分别平分∠ABC、∠ADC的外角，写出BF与DE的位置关系，并证明．

（第1题图）（第2题图）

2，如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数和．

3，如图在平面直角坐标系中，直线AB交y轴于点C,连接OB

（1）若A（-1,0）,B（1,2）求三角形AOB的面积

如图所示，在平面直角坐标系中，AB交y轴于点C，连接OB．

（1）如图①所示，已知A（﹣2，0），B（2，4），求△AOB的面积；

（2）如图②所示，点D在x轴上，∠OBD=∠OBC，求的值；

（3）如图③所示，BM⊥x轴于点M，N在y轴上，∠MNB=∠MBN，点P在x轴上，∠MNP=∠MPN，求∠BNP的度数．

二，《轴对称》与《全等三角形》部分；

4，已知∠MAN，AC平分∠MAN．

（1）在图1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：

AB+AD=AC；

（2）在图2中，若∠MAN=120°，∠ABC+∠ADC=180°，则

（1）中的结论是否仍然成立？

若成立，请给出证明；若不成立，请说明理由．

5，已知△ABC，分别以AB、AC为边作△ABD和△ACE，且AD=AB，AC=AE，∠DAB=∠CAE，连接DC与BE，G、F分别是DC与BE的中点．

（1）如图1，若∠DAB=60°，则∠AFG=　　；

（2）如图2，若∠DAB=90°，则∠AFG=　　；

（3）如图3，若∠DAB=α，试探究∠AFG与α的数量关系，并给予证明．

6,如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD，给出四个结论：

①∠ADC=45°；②BD=AE；③AC+CE=AB；④AB﹣BC=2MC；其中正确的结论有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

如图，∠BAC=110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（　　）

A．

20°

B．

40°

C．

50°

D．

60°

如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D．

①求证：

AD是∠BAC的平分线；

②求∠ADC的度数；

③求证：

点D在AB的中垂线上；

④求证：

S△DAC：

S△ABC=1：

3．

已知，在等腰Rt△ABC中，∠ABC=90°，AB=CB，D为直线AB上一点，连接CD，过C作CE⊥CD，且CE=CD，连接DE，交AC于F．

（1）如图1，当D、B重合时，求证：

EF=BF．

（2）如图2，当D在线段AB上，且∠DCB=30°时，请探究DF、EF、CF之间的数量关系，并说明理由．

（3）如图3，在

（2）的条件下，在FC上任取一点G，连接DG，作射线GP使∠DGP=60°，交∠DFG的角平分线于点Q，求证：

FD+FG=FQ．

如图，D是等边△ABC外的一点，DB=DC，∠BDC=120°，且E、F分别在AB和AC上．

（1）求证：

AD是BC的垂直平分线；

（2）若ED平分∠BEF，证明：

①FD平分∠EFC；

②△AEF的周长是BC长的2倍．

（2013•溧水县二模）如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，求BC．

下列手机屏幕解锁图案中不是轴对称图形的是（　　）

A．

B．

C．

D．

如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A=60°，∠1=95°，则∠2的度数为（　　）

A．

24°

B．

25°

C．

30°

D．

35°

如图△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：

（1）△ACE≌△DCB；

（2）CM=CN；（3）MN∥AB；（4）AC=DN，其中正确结论的个数是（　　）A．1个B．2个C．3个D．4个

如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，且A、C、B在同一直线上，有如下结论：

①△ACE≌△DCB；　②CM=CN；③AC=DN；④PC平分∠APB；⑤∠APD=60°．其中不正确结论是．（填序号）

13，如图，△ABC中，AB=AC，∠BAC=56°，∠BAC的平分线与AB的垂直平分线OD交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC度数为　_________　°．

如图，△ABC中，AB=AC，∠BAC=56°，∠BAC的平分线与AB的垂直平分线OD交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC度数为　_________　°．

如图，已知等边△ABC中，D为AC上一动点．CD=nAD，连接BD，M为线段BD上一点，∠AMD=60°，AM交BC于E．

（1）若n=1，如图1，则=，=

（2）

（2）若n=2，如图2，求证：

2AB=3BE；

（3）当时，则n的值为

如图，点D是等边△ABC外一点，且DB=DC，∠BDC=120°，将一个三角尺60°的顶点放在点D上，三角尺的两边DP、DQ分别与射线AB、CA相交于E、F两点．

（1）当EF∥BC时，如图①，证明：

EF=BE+CF；

（2）当三角尺绕点D旋转到如图②的位置时，线段EF、BE、CF之间的上述数量关系是否成立？

如果成立，请给予证明；如果不成立，写出EF、BE、CF之间的数量关系，并说明理由；

（3）当三角尺绕点D继续旋转到如图③的位置时，

（1）中的结论是否发生变化？

如果不变化，直接写出结论；如果变化，请直接写出EF、BE、CF之间的数量关系．

如图，∠ABD、∠ACD的角平分线交于点P，若∠A=50°，∠D=10°，则∠P的度数为

一，《分式》练习题

1,某人骑自行车匀速爬上一个斜坡后立即匀速下坡回到出发点，若上坡速度为为每小时V1千米，下坡时的速度为每小时V2千米，则他在这段路上、下坡的平均速度是

ABCD

2,若,则的值为

3,若，，，则的值为（用含m的代数式表示）

4,已知的值

5,（2012•东莞）观察下列等式：

第1个等式：

a1==×（1﹣）；

第2个等式：

a2==×（﹣）；

第3个等式：

a3==×（﹣）；

第4个等式：

a4==×（﹣）；

…请解答下列问题：

（1）按以上规律列出第5个等式：

a5=　　；

（2）用含有n的代数式表示第n个等式：

an=　　=　　（n为正整数）；

（3）求a1+a2+a3+a4+…+a100的值．

先阅读下列材料，在解答后面的问题；上述题中用到的是‘整体思想’

阅读下列材料解答下列问题：

观察下列方程：

①；②；③

（1）按此规律写出关于x的第n个方程为　　，此方程的解为　　．

（2）根据上述结论，求出x+的解．

初中数学课本中有这样一段叙述,“要比较a与b的大小，可以先求出a与b的差，再看这个差是正数，负数还是零”有一块直径为2a+2b的圆形钢板（a≠b）现在要挖去两个圆．

方案一：

挖去直径分别为2a，2b的两个圆；

方案二：

挖去直径都为a+b的两个圆．

设方案一、方案二剩下钢板的面积分别为M，N．

（1）分别用字母a，b表示M、N的值；

（2）比较M、N的大小．

（2011•古冶区一模）请先阅读下列一段文字，然后解答问题：

有这样一段叙述：

“要比较a与b的大小，可以先求出a与b的差，再看这个差是正数、负数还是零，”由此可见，要判断两个代数式值的大小，只要考虑它们的差就可以．

问题：

甲、乙两人两次同时在同一粮店购买粮食（假设两次购买粮食的单价不相同）甲每次购买粮食100kg，乙每次购粮用去100元．

（1）设第一、第二次购粮单价分别为x元/kg和y元/kg，用含x、y的代数式表示：

甲两次购买粮食共需付粮款元，乙两次共购买kg粮食．若甲两次购粮的平均单价为每千克q1元，乙两次购粮的平均单价和每千克q2元，则q1=，q2=

（2）若规定：

谁两次购粮的平均单价低，谁的购粮方式就更合算，请你判断甲、乙两人的购粮方式哪一个更合算，并说明理由．

若关于x的分式方程﹣1=无解，则m的值．

研究问题经常采用由特殊到一般的方法．在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象

进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征．

（1）比较下列各式的大小．

．．．

（2）比较原来每个分数对应新分数的大小，可以得出下面的结论：

一个真分数是（a，b均为正数），给其分子分母同加一个正数m，得，

则两个分数的大小关系是．

①请你用文字叙述

（2）中结论的含义：

②请用图形的面积说明这个结论．

整式的乘法与因式分解

因式分解1,2,

3,4，

5，6，

7，8，

先阅读下面的内容，再解决问题，

例题：

若m2+2mn+2n2﹣6n+9=0，求m和n的值．

解：

∵m2+2mn+2n2﹣6n+9=0

∴m2+2mn+n2+n2﹣6n+9=0

∴（m+n）2+（n﹣3）2=0

∴m+n=0，n﹣3=0

∴m=﹣3，n=3

问题

（1）若x2+2y2﹣2xy+4y+4=0，求xy的值．

（2）已知a，b，c是△ABC的三边长，满足a2+b2=10a+8b﹣41，且c是△ABC中最长的边，求c的取值范围．

先阅读材料，再回答问题：

材料：

分解因式：

（x+y）2+2（x+y）+1

解：

将“x+y”看成整体，令x+y=A，则原式=A2+2A+1=（A+1）2，再将“A”还原，原式=（x+y+1）2．上述解题中用到的是“整体思想”，整体思想是数学中常用的一种思想，你能用整体思想回答下列问题吗？

问题：

（1）分解因式：

（a+b）（a+b﹣4）+4．

（2）求证：

若n为正整数，则代数式n（n+1）（n+2）（n+3）+1的值一定是某一个整数的平方．

（2009•河池）铭润超市用5000元购进一批新品种的苹果进行试销，由于销售状况良好，超市又调拨11000元资金购进该品种苹果，但这次的进货价比试销时每千克多了0.5元，购进苹果数量是试销时的2倍．

（1）试销时该品种苹果的进货价是每千克多少元？

（2）如果超市将该品种苹果按每千克7元的定价出售，当大部分苹果售出后，余下的400千克按定价的七折（“七折”即定价的70%）售完，那么超市在这两次苹果销售中共盈利多少元？

如图（自己画图）所示，直线AB与Y轴正半轴交与A（0,a）与X轴正半轴交与B（b,0）

（1）若a+b=4,且，求三角形AOB的面积

（2）若分式无意义，AC平分角OAB交X轴于C,求证;

（3）在

（2）的条件下，过O作OD垂直AC于D点，求的值

在平面直角坐标系中，A（-1,-1）B（3,3）,若M为x轴上的点，且MA+MB最小，则M的坐标是

（2013•张家界）阅