计算机图形学实验报告Word文件下载.docx
《计算机图形学实验报告Word文件下载.docx》由会员分享,可在线阅读,更多相关《计算机图形学实验报告Word文件下载.docx(20页珍藏版)》请在冰豆网上搜索。
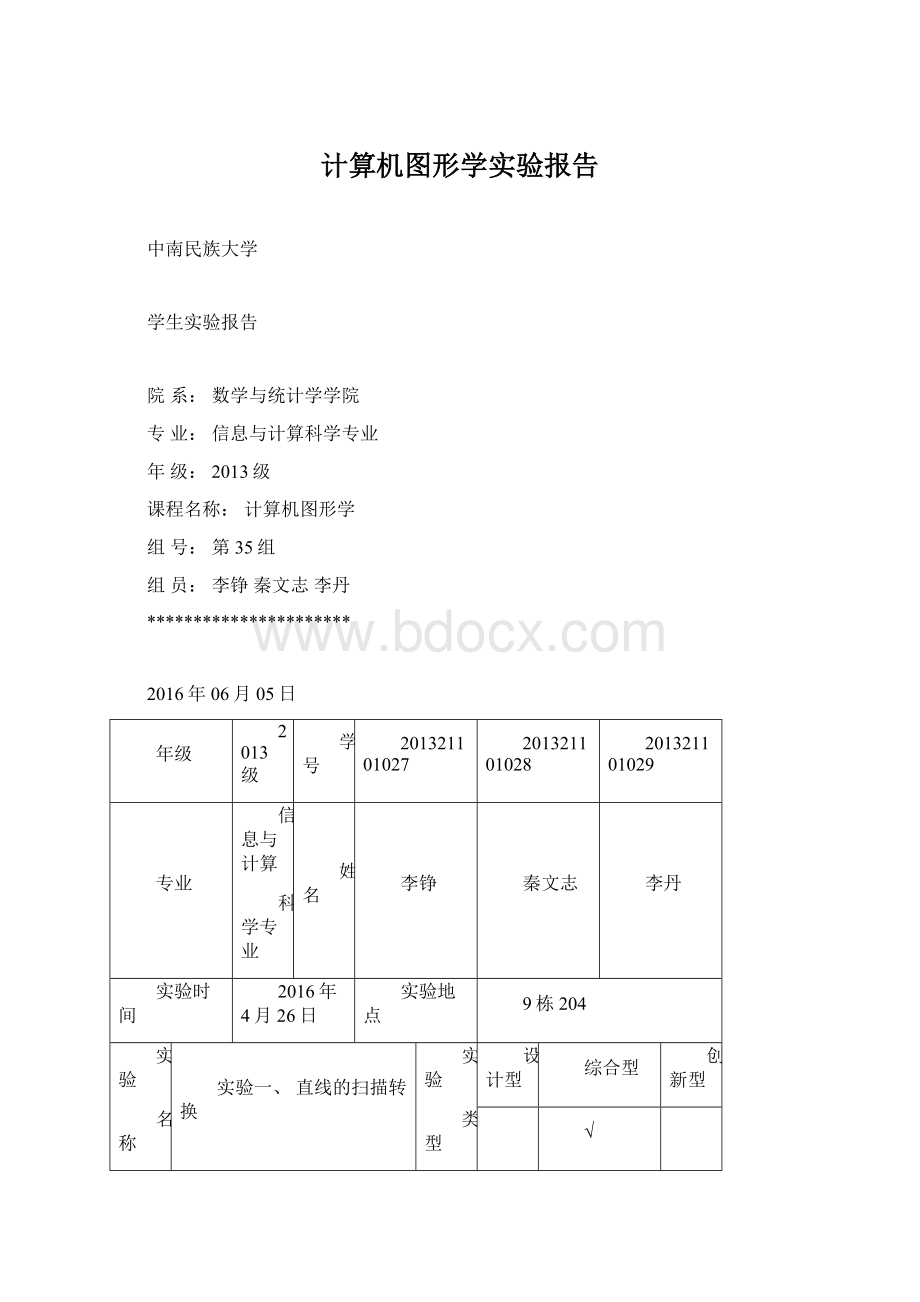
姓名
李铮
秦文志
李丹
实验时间
2016年4月26日
实验地点
9栋204
实验
名称
实验一、直线的扫描转换
类型
设计型
综合型
创新型
√
实
验
目
的
1)理解在显示器上画图与在纸上画图的本质区别;
2)掌握直线的光栅扫描转换过程;
3)掌握不同算法绘制直线的思路和优缺点。
要
求
用基本增量算法和Bresenham算法画直线
1)将像素网格表现出来,建立网格坐标系;
2)显示判别式的计算过程和下一点的选择策略;
3)记录生成点的坐标,建议用表的形式;
4)图形生成过程可以重复进行。
原
理
DDA代码:
clear
closeall
clc
x1=0;
y1=0;
x2=15;
y2=12;
figure,line([x1,x2],[y1,y2],'
Color'
[001]);
length=abs(x2-x1)+1;
dx=(x2-x1)/length;
dy=(y2-y1)/length;
k=dy/dx;
x=x1;
y=y1;
holdon
fori=1:
length
plot(round(x),floor(y+0.5),'
*r'
)
x=x+1;
y=y+k;
end
holdoff
Bresenham代码:
dx=x2-x1;
dy=y2-y1;
e=2*dy-dx;
holdon
fori=1:
if(e>
=0)
y=y+1;
e=e-2*dx;
end
x=x+1;
e=e+2*dy;
holdoff
结
果
分
析
Bresenham法:
心
得
体
会
成
绩
评
定
教师签名:
年月日
2016年5月3日
实验二、圆弧的扫描转换
1)掌握圆和圆弧的光栅扫描转换过程;
2)掌握不同算法绘制圆弧的技巧和优缺点。
用正负法和Bresenham算法画圆弧
Bresenham算法:
functionbresenham(b)
x=0;
y=b;
d=3-2*b;
theta=0:
0.01*pi:
2*pi;
x1=b*cos(theta)+0;
y1=b*sin(theta)+0;
plot(x1,y1);
holdon
plot(0,0,'
b+'
);
holdon;
whilex<
y
{plot(x,y,'
*'
plot(-x,-y,'
plot(-x,y,'
plot(x,-y,'
}
ifd<
d=d+4*x+6;
else
d=d+4*(x-y)+10;
y=y-1;
if(x==y)
plot(x,y,'
plot(-x,-y,'
holdoff;
正负法:
functionzf(b)
f=0;
whiley>
iff>
f=f-2*y+1;
f=f+2*x+1;
if(y==0)
2016年5月17日
实验三、直线段的裁剪
用Cohen-SutherLand算法和liang_barsky算法进行线段裁剪
1)理解裁剪的相关概念
2)掌握直线段的一般裁剪过程;
3)理解并掌握Cohen-SutherLand算法的编码思想;
4)理解并掌握Liang_Barsky算法的参数化裁剪思想;
2)交互输入剪裁线段和裁剪窗口;
3)对于线段裁剪,线段被窗口的四条边裁剪的过程要显示出来;
4)裁剪过程可以重复进行。
Cohen-SutherLand算法核心代码:
functionLines=Cohen_Sutherland(line,Rectangle)
%编码裁剪算法
%line为线段端点矩阵,共四列,其数据含义如下:
%端点Ax坐标端点Ay坐标端点Bx坐标端点By坐标
%Rectangle为窗口边界值,共四个元素,其含义分别为Xwl,Xwr,Ywb,Ywt。
%
%首先检测参数是否合法
[rowcolumn]=size(line);
ifcolumn<
4||length(Rectangle)<
4
Lines=[];
fprintf('
参数不合法不合法'
return;
%程序中主要变量说明
%code为线段端点的编码矩阵,两行四列,第一行为点P1的编码,第二行为点P2的编码
%四列的含义为:
D0,D1,D2,D3
%依次处理line的各个线段
k=0;
length(line(:
1))
%取出第i条线段
P1=line(i,[1,2]);
P2=line(i,[3,4]);
%计算斜率
PP=P1-P2;
ifPP
(1)==0
k=inf;
else
k=PP
(2)/PP
(1);
finished=false;
while(~finished)
%对点P1和P2进行编码
code=[
P1
(1)<
Rectangle
(1),P1
(1)>
Rectangle
(2),P1
(2)<
Rectangle(3),P1
(2)>
Rectangle(4);
P2
(1)<
Rectangle
(1),P2
(1)>
Rectangle
(2),P2
(2)<
Rectangle(3),P2
(2)>
];
%P1,P2,k,code
%进行简取或简弃的判断
test=code(1,:
)|code(2,:
%判断是否简取
ifisempty(find(test>
0,1))
Lines=[Lines;
[P1,P2]];
finished=true;
%若当前线段处理完成,则退出
iffinished
break;
%判断是否简弃
)&
code(2,:
if~isempty(find(test>
0,1))
%确保P1在窗口之外
ifisempty(find(code(1,:
)>
%交换P1,P2的坐标值和编码
PT=P1;
P1=P2;
P2=PT;
PT=code(1,:
code(1,:
)=code(2,:
)=PT;
%从低位开始找编码值为1的地方
D=find(code(1,:
0,1);
ifD<
=2
%此时P1位于窗口的左边或右边
ifk==0
%若是水平线,则y不变,x变为窗口的左边界或右边界
%且此时k不会等于inf,否则线段处于简弃状态。
P1
(1)=Rectangle(D);
%P1
(2)=Rectangle(find(code(1,[3,4])>
0,1));
%若线段是斜线,则计算y值,x值变为窗口的左边界或右边界
P1=[Rectangle(D),P1
(2)+k*(Rectangle(D)-P1
(1))];
%此时P1位于窗口的上方或下方
ifk==inf
%若线段是竖直线,则x不变,y变为窗口的上边界或下边界
%且此时k不会等于0,否则线段将处于简弃状态。
P1
(2)=Rectangle(D);
%若线段是斜线,则计算x值,y值变为窗口的上边界或下边界。
P1=[P1
(1)+(Rectangle(D)-P1
(2))/k,Rectangle(D)];
%对P1和P2重新编码,再次计算。
%pause(10);
%scanf(D,'
%d'
%inputdlg('
'
%对最终点进行取整运算
%Lines=round(Lines);
Cohen-SutherLand算法:
年