高三数学复习计划Word文档下载推荐.doc
《高三数学复习计划Word文档下载推荐.doc》由会员分享,可在线阅读,更多相关《高三数学复习计划Word文档下载推荐.doc(6页珍藏版)》请在冰豆网上搜索。
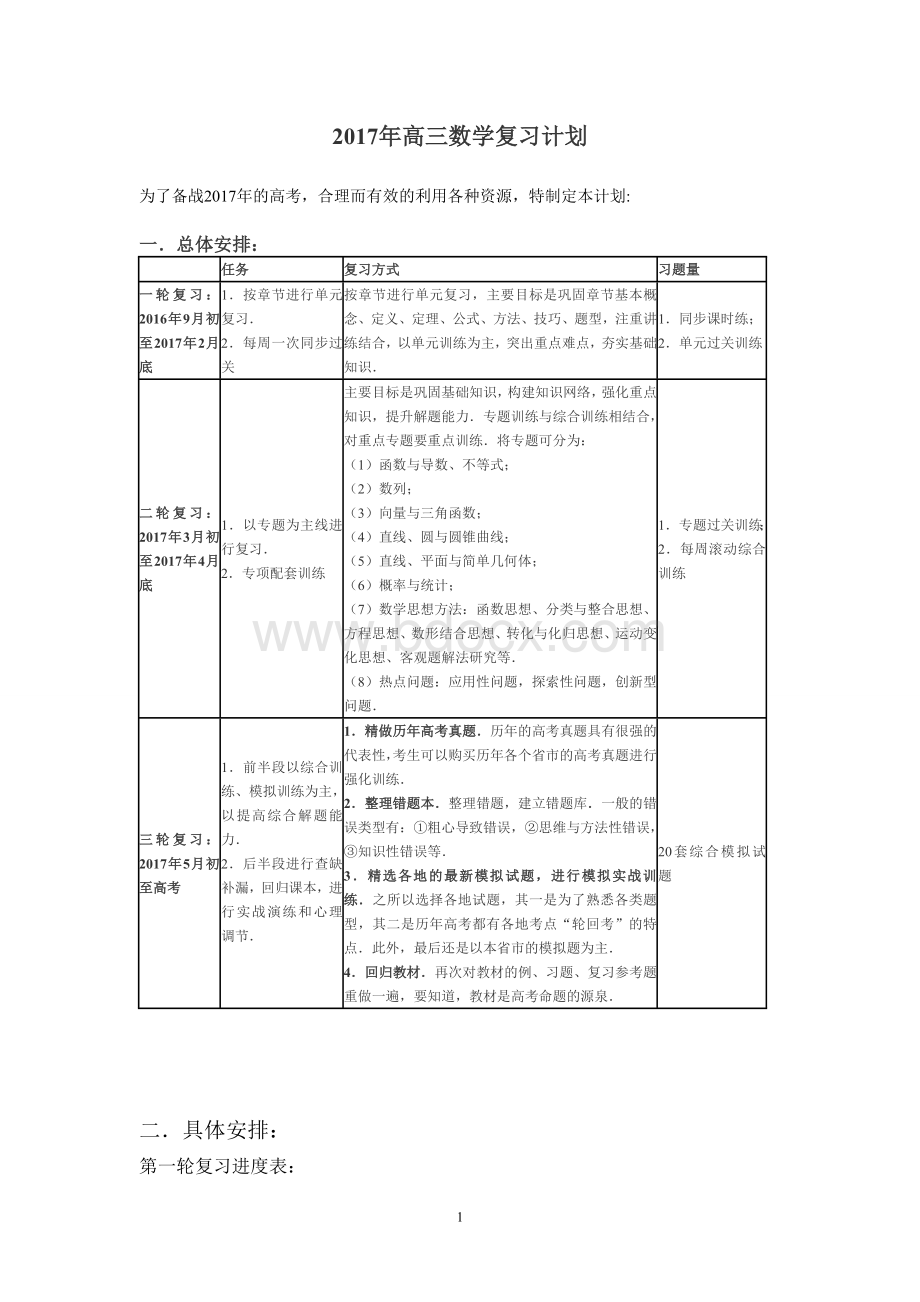
(5)直线、平面与简单几何体;
(6)概率与统计;
(7)数学思想方法:
函数思想、分类与整合思想、方程思想、数形结合思想、转化与化归思想、运动变化思想、客观题解法研究等.
(8)热点问题:
应用性问题,探索性问题,创新型问题.
1.专题过关训练;
2.每周滚动综合训练
三轮复习:
2017年5月初至高考
1.前半段以综合训练、模拟训练为主,以提高综合解题能力.
2.后半段进行查缺补漏,回归课本,进行实战演练和心理调节.
1.精做历年高考真题.历年的高考真题具有很强的代表性,考生可以购买历年各个省市的高考真题进行强化训练.
2.整理错题本.整理错题,建立错题库.一般的错误类型有:
①粗心导致错误,②思维与方法性错误,③知识性错误等.
3.精选各地的最新模拟试题,进行模拟实战训练.之所以选择各地试题,其一是为了熟悉各类题型,其二是历年高考都有各地考点“轮回考”的特点.此外,最后还是以本省市的模拟题为主.
4.回归教材.再次对教材的例、习题、复习参考题重做一遍,要知道,教材是高考命题的源泉.
20套综合模拟试题
二.具体安排:
第一轮复习进度表:
周次
课时
复习时间
复习内容
1
5
8.2---8.6
1.集合的概念与运算(2课时)
2.命题及其关系(2课时)
3.逻辑连接词(1课时)
2
8.7---8.11
1.函数及其表示(3课时)
2.函数的单调性及最值(2课时)
3
8.12---8.16
1函数的奇偶性与周期性(3课时)
2.指数与指数函数(2课时)
4
9.1——9.7
1.对数与对数函数(3课时)
2.幂函数及二次函数(2课时)
9.8---9.14
1.函数的图象及其变换(3课时)
2.函数与方程(2课时)
6
9.15---9.21
1.导数与导数的计算(2课时)
2.导数的应用(3课时)
7
9.22---9.28
1.微积分基本定理(2课时)
2.任意角的弧度制及三角函数(2课时)
3.同角三角函数的基本关系及诱导公式(2课时)
8
9.29---10.12
1.三角函数的图象及其性质(3课时)
2.简单的三角恒等变换(2课时)
9
10.13---10.19
1.正余弦定理及应用举例(3课时)
2.平面向量的概念及线性运算(2课时)
10
10.20---10.26
1.平面向量基本定理及坐标运算(2课时)
2.平面向量的数量积及应用(2课时)
3.数系的扩充与复数的应用(1课时)
11
10.27---11.2
1.数列的概念及表示方法(3课时)
2.等差数列及其前n项和(2课时)
12
11.3---11.9
1.等比数列及其前n项和(2课时)
2.数列求和(2课时)
3.不等关系与不等式(1课时)
13
11.10---11.16
1.一元二次不等式及其解法(2课时)
2.线性规划(2课时)
3.基本不等及应用(2课时)
14
11.17—11.23
1.空间几何体的结构及三视图(2课时)
2.空间几何体的表面积、体积(2课时)
15
11.24---11.30
1.平面的基本性质(2课时)
2.线性平面的判定及性质(2课时)
3.线性垂直的判定及性质(2课时)
16
12.1---12.7
1.空间向量的应用(3课时)
2.直线及其方程(2课时)
17
12.8---12.14
1.两条直线的位置关系(2课时)
2.圆的方程(2课时)
3直线与圆(2课时)
18
12.15---12.21
1.椭圆(3课时)
2.双曲线(2课时)
19
12.22---12.28
1.抛物线(3课时)
2.直线与圆锥曲线(2课时)
20
12.29---1.5
1.曲线与方程(2课时)
2.算法与程序框图(1课时)
3.随机抽样(1课时)
4.用样本估计总体(1课时)
21
1.6---1.12
1.变量间的相关关系与统计案例(1课时)
2.分类加法与分步乘法原理(2课时)
3.排列与组合(2课时)
22
1.13---1.19
1.二项式定理(1课时)
2.事件与概率(2课时)
3.古典概型与几何概型(2课时)
23
1.20---1.26
1.离散型随机变量及分布列(2课时)
2.二项分布、正态分布及应用(2课时)
3.均值与方差(2课时)
24
1.27---1.28
1.坐标系与参数方程(2课时)
第二轮及第三轮复习进度表:
时间
课时
1-2
3.2-3.15
1.三角函数(5课时)
2.解三角形(5课时)
3.16-3.24
1.数列的通项(4课时)
2.数列的求和(3课时)
4-5
3.25-4.7
1.概率与统计(5课时)
2.几种特殊分布(5课时)
4.8-4.13
1.极坐标及参数方程(2课时)
2.不等式(2课时)
4.14-4.22
1.立体几何的证明(4课时)
2.立体几何中的角与距离(3课时)
4.23-4.30
1.解析几何之方程与轨迹(3课时)
2.直线与圆锥曲线(3课时)
5.4-5.11
1.函数导数不等式(3课时)
2.恒成立问题(3课时)
5.12-6.2
经典模拟试题讲练
备考建议:
一、制订备考计划,确定备考原则
第一阶段:
2016年7月至2017年2月,本阶段主要任务是系统巩固,基础知识、基本技能、基本方法的全面复习。
一方面,高考的第一阶段复习必须真正地回到课本,回到基础中去,澄清基本概念,对于课本上的每一个定义任一定理所有公式都要熟透于心理解它的本质,变化与应用;
另一方面,在复习中必须切实克服“眼高手低”的毛病,不好高骛远,毫不吝惜地删除某些复习资料中的偏题、难题和怪题,同时,以课本的习题为素材,深入浅出、举一反三地加以推敲、延伸和适当变形,形成典型例题,借助于启发式讲解来帮助学生融会贯通基础知识;
再之,必须将讲与练结合起来,借助于周周练和模拟考试(题目应切实根据学生的实际编拟)来进一步夯实基础。
对于数学优生也只是适量做一些热点综合题,决不可抛开基础于不顾,单纯追求高难度.
第二阶段:
2017年3月至4月底,本阶段主要任务是专题过关建立各模块的深层联系,渗透数学思想方法,培养综合运用能力。
摘取近5年的数学高考试题在加强基础知识考查的同时,本阶段主要讲解六专题(函数与导数不等式;
三角函数;
空间几何体;
直线与圆的方程及圆锥曲线;
概率与统计,选考内容)以及五种数学思想(函数与方程的思想,数与形结合的思想,分类讨论的思想,化归与转化的思想,特殊与一般的思想),指导学生巩固第一阶段成果,拔高能力.
第三阶段:
2017年5月至6月2日,本阶段主要任务是冲刺卷训练,模拟高考,收好关子,缩小目标,集中火力,培训应试技巧和各种非智力因素,清理哪些谷粒能够归仓,哪些内容和题形能够再多拿几分.
二.仔细研究考试大纲,了解高考新动向
大家都知道《考试大纲》对高三备考的参考价值,它是高考的导航灯和牵引线,给我们明确了考试的范畴和重心。
因此我们在拿到《2017年考试大纲》后,备课组进行集体研读,让每名成员对大纲内容至少有整体的把握,然后,将其与2016年的大纲进行比对,找出其中的差异与变化。
三.确定重点内容和热点内容,轻重把握得当,时间分配合理。
重点内容有:
函数、三角、数列、解析几何、立体几何,这些内容是高考数学试卷的骨架,所占分值高,题源丰富,题形灵活,是考查数学知识和考查数学能力的最主要素材,是备考重中之重;
热点内容有:
导数及其应用、平面向量、概率、统计、算法初步、坐标系与参数方程(或平面几何选讲),这些内容的考题定位在容易题和中档题,容易拿分,复习效果好,投入必有产出。
四.值得肯定的几种做法:
第一、坚持每周集体备课,中心发言人轮值,交流备考体会,交流学生学习情况,及时发现学生在复习备考中出现的问题,及时调整备考策略;
研究考纲、考题,研究学生学习情况、学习状态,研究周周练试卷反映的问题,研究复习内容的深度和广度,研究选讲哪些例题和习题,等等。
第二、模拟考试,考题内容为复习过的所有内容,滚动复习,避免遗忘,要求老师改卷评卷并作好成绩统计和分析,跟踪学生成绩,关注测验成绩出现大起大落的学生;
考完后老师选编针对性训练作为练习,印发给学生做作业。
五.加强学法和解题技巧的指导,提高学生的应试能力
复习中,我们还加强了学生的学法指导,主要从以下几个方面:
(1)要求学生养成良好的审题习惯,提高阅读能力。
审题是解题的关键,数学题是由文字语言、符号语言和图形语言构成的,拿到题要“宁停三分,不抢一秒”,要在已有知识和解题经验的基础上,逐字逐句的仔细审题,细心推敲,将隐含条件转化为明显条件,有时须联系题设和结论,寻找突破口,从而形成解题思路。
(2)要求学生养成解后反思,归纳总结的习惯,提高分析和概括问题的能力。
解完题后,要不失时机地回顾下列问题,如何分析、联想、探索出解题途径的?
问题获得解决的关键是什么?
通过解题后的回顾和反思,就有利于发现解题的关键所在,并从中提炼出数学思想和方法,提高分析问题和解决问题的能力。
(3)要求学生养成纠错订正的习惯,提高自我评判能力。
对做错的题要反复琢磨,寻找错因,写出心得,进行更正,日积月累,反复查看。
不少问题就会豁然开朗,避免以后犯同样的错误。