高二数学上学期期末考试试题 理Word文件下载.docx

高二数学上学期期末考试试题 理Word文件下载.docx

《高二数学上学期期末考试试题 理Word文件下载.docx》由会员分享，可在线阅读，更多相关《高二数学上学期期末考试试题 理Word文件下载.docx（10页珍藏版）》请在冰豆网上搜索。

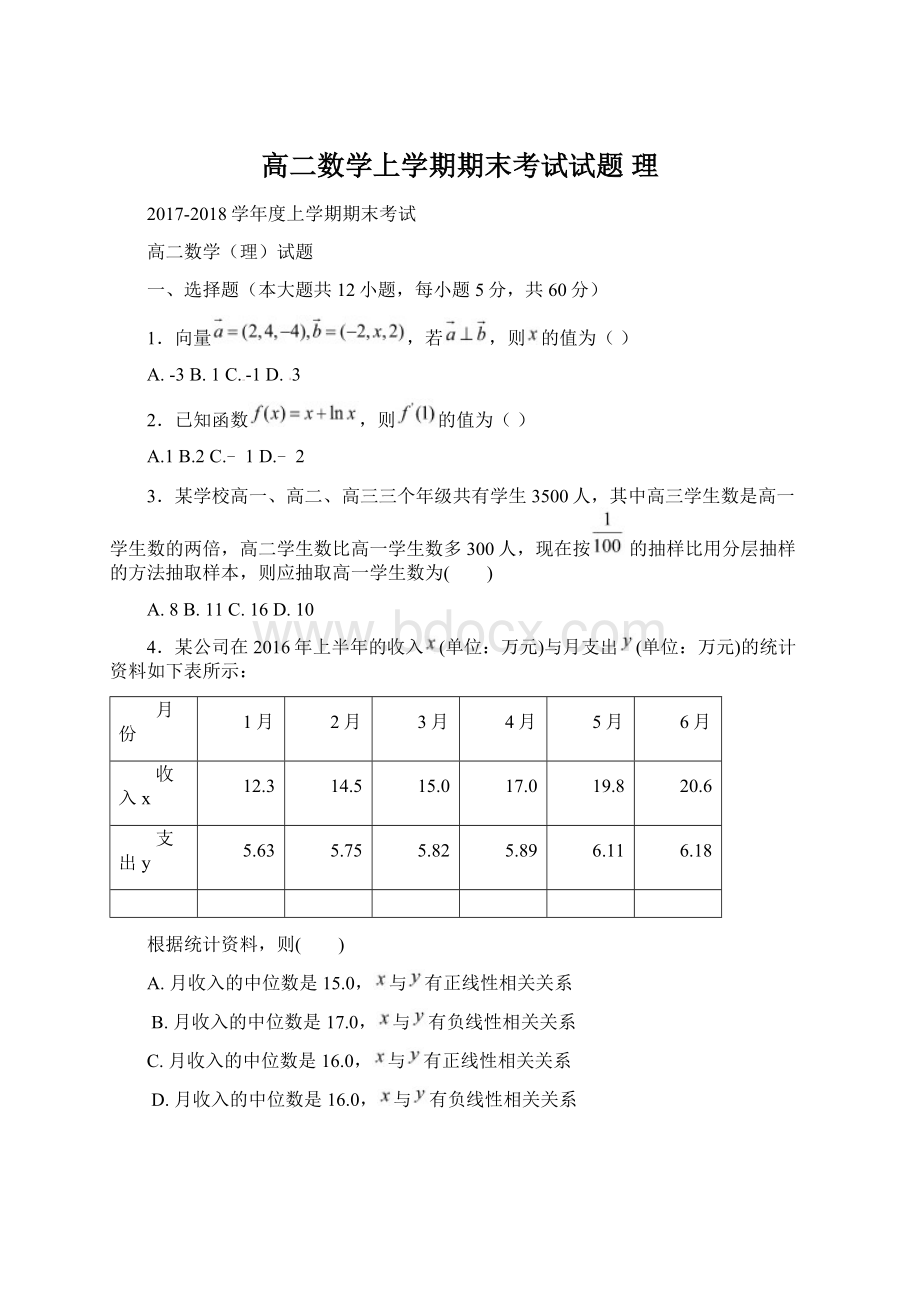
3月

4月

5月

6月

收入x

12.3

14.5

15.0

17.0

19.8

20.6

支出y

5.63

5.75

5.82

5.89

6.11

6.18

根据统计资料，则（　　）

A.月收入的中位数是15.0，与有正线性相关关系

B.月收入的中位数是17.0，与有负线性相关关系

C.月收入的中位数是16.0，与有正线性相关关系

D.月收入的中位数是16.0，与有负线性相关关系

5．齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛，则田忌的马获胜的概率为（）

A.B.C.D.

6．点集，，在点集中任取一个元素，则的概率为（）

7．下列说法错误的是（）

A.“函数为奇函数”是“”的充分不必要条件

B.已知三点不共线，若则点是△的重心

C.命题“，”的否定是：

“，”

D.命题“若，则”的逆否命题是：

“若，则”

8．过双曲线的右焦点且垂直于轴的直线与双曲线交于两点，为虚轴上的一个端点，且为直角三角形，则此双曲线离心率的值为（）

A.B.C.或D.或

9．若双曲线的焦距4，则该双曲线的渐近线方程为（）

10．已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦

等于（）．

11．设函数在区间上单调递减,则实数的取值范围是（）

12．设函数．若存在的极值点满足，则的取值

范围是（）

A.B.

C.D.

二、填空题（本大题共4个小题，每小题5分，共20分）

13．已知命题“”为假命题，则实数的取值范围是_______

14．由动点向圆引两条切线、切点分别为、，若，则动

点的轨迹方程为__________．

15．执行如图所示的程序框图，输出的值是__________．

16．已知函数（为自然对数的底数），若，则实数的取值范围是___________．

三、解答题（本大题共6个小题，17题10分，其余各题各12分，共70分）

17．（本小题满分10分）已知过抛物线的焦点，斜率为的直线交抛物线于

两点.

（1）求线段的长度；

（2）为坐标原点,为抛物线上一点，若，求的值．

18．（本小题满分12分）已知关于的二次函数

（Ⅰ）设集合和，分别从集合，中随机取一个数作为和，求函数在区间上是增函数的概率．

（Ⅱ）设点是区域内的随机点，求函数在区间上是增函数的概率．

19．（本小题满分12分）已知四棱锥，底面是边长为的菱形，，为的中点，，且

（1）在棱上求一点，使平面；

（2）求二面角的余弦值.

20．（本小题满分12分）已知函数，曲线在点处的切线方程为

（1）求的值；

（2）求的极大值.

21．（本小题满分12分）已知椭圆的两个焦点分别为，，点与椭圆短轴的两个端点的连线相互垂直.

（1）求椭圆的方程；

（2）过点的直线与椭圆相交于两点，设点，记直线的斜率分别为，求证：

为定值.

22．（本小题满分12分）设函数

（1）当，恒成立，求实数的取值范围.

（2）设在上有两个极值点.

（A）求实数的取值范围；

（B）求证：

.

2017高二上学期期末数学参考答案（理）

1-12DBACABADDAAC

13．14．15．16．

17．解：

（1）直线AB的方程是y＝2（x-2），与y2＝8x联立，消去y得x2－5x＋4＝0，

由根与系数的关系得x1＋x2＝5.由抛物线定义得|AB|＝x1＋x2＋p＝9，

（2）由x2－5x＋4＝0，得x1＝1，x2＝4，从而A（1，－2），B（4，4）．

设＝（x3，y3）＝（1，－2）＋λ（4，4）＝（4λ＋1，4λ－2），

又y＝8x3，即[2（2λ－1）]2＝8（4λ＋1），即（2λ－1）2＝4λ＋1，解得λ＝0或λ＝2.

18．解：

要使函数在区间上是增函数，需且，即且．

（Ⅰ）所有的取法总数为个．满足条件的有，，，，共5个，

所以所求概率．

（Ⅱ）如图，求得区域的面积为．

由，求得．所以区域内满足且的面积为．

所以所求概率

19．

解:

（1）以为轴，为轴，与的交点为，过作平面的垂线为轴，建立空间直角坐标系.其中：

，，，，，

设，，

则：

.

设平面的法向量为，，

所以故.

，所以，因此，所以为中点.

（2）平面的法向量，

平面的法向量，

由二面角为锐二面角，

因此，二面角的余弦值为.

20．解：

（1）由已知得,据此可知：

（2）由

（1）知

令，则令得递增区间为

令得递减区间为所以时，取得极大值，

21．解：

（1）依题意，，.

∵点与椭圆短轴的两个端点的连线相互垂直，

∴，∴.

∴椭圆的方程为.

（2）①当直线的斜率不存在时，由解得，.

设，，则为定值.

②当直线的斜率存在时，设直线的方程为：

将代入整理化简，得.

依题意，直线与椭圆必相交于两点，设，，则，.

又，，

所以

.

综上得为常数2.

22．解：

（1）∵，且，∴.

令，则.

①当时，，在上为单调递增函数，

∴时，，不合题意.

②当时，时，，在上为单调递增函数，

∴，，不合题意.

③当时，，，在上为单调递减函数.

④当时，，，在上为单调递增函数.

，，在上为单调递减函数.∴，符合题意.

综上，.

（2），..

令，则

由已知在上有两个不等的实根.

（A）①当时，，在上为单调递增函数，不合题意.

②当时，，在上为单调递减函数，不合题意.

③当时，，，，，

所以，，，，解得.

（B）由已知，，∴.

不妨设，则，

则.

令，.

则，

∴在上为单调递增函数，

∴

即，∴，

∴，∴，

由（A），∴，

∴.