王宝林讲义选修33《气体》题型归类汇总Word格式文档下载.docx

王宝林讲义选修33《气体》题型归类汇总Word格式文档下载.docx

《王宝林讲义选修33《气体》题型归类汇总Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《王宝林讲义选修33《气体》题型归类汇总Word格式文档下载.docx（19页珍藏版）》请在冰豆网上搜索。

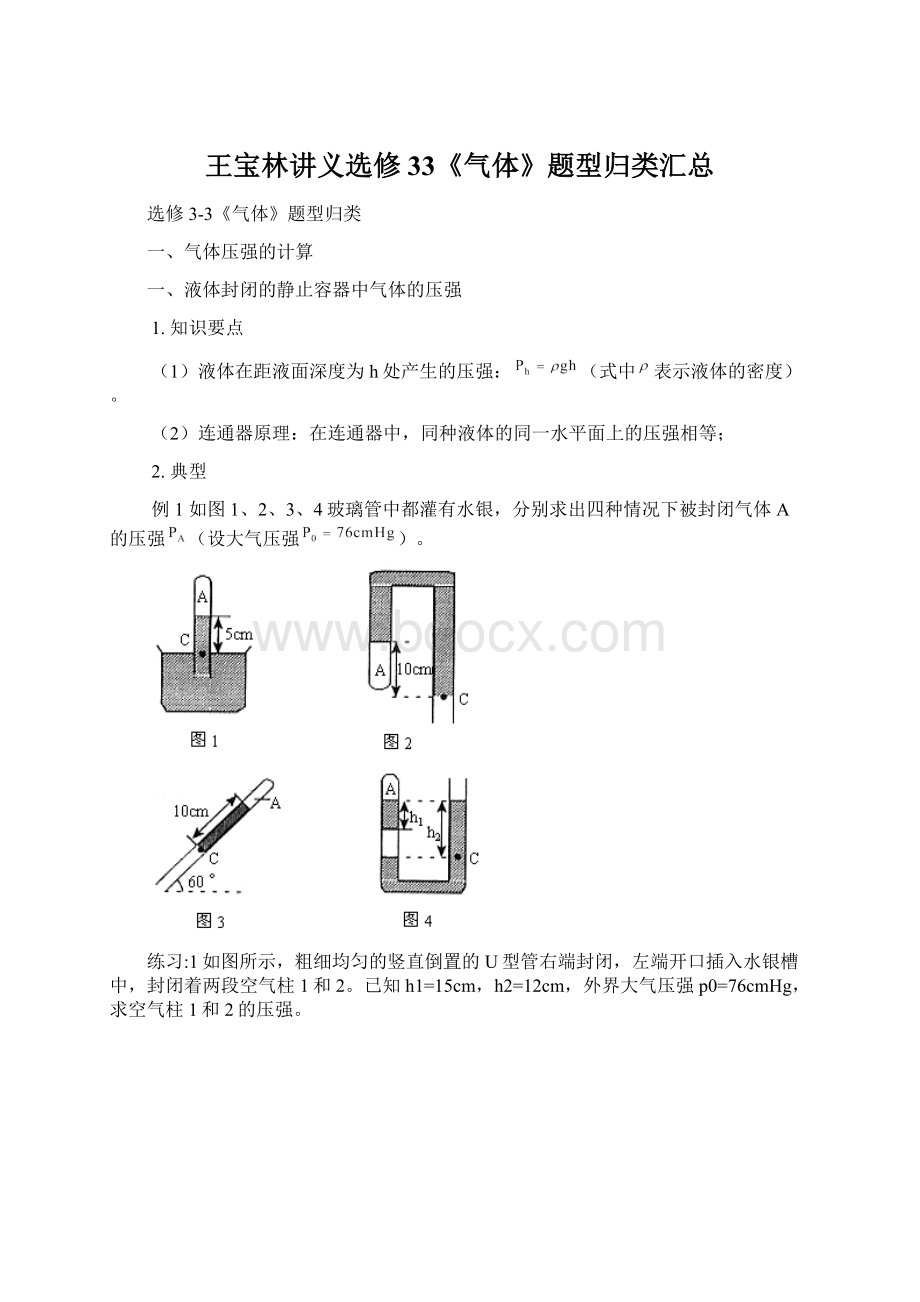
若管中向上将玻璃管放置在一个倾角为30°

的光滑斜面上。

在下滑过程中被封闭气体的压强（设大气压强为P0=76cmHg）为（ 

）

A.76cmHg 

B.82cmHg

C.88cmHg 

D.70cmHg

二、活塞封闭的静止容器中气体的压强

1.解题的基本思路

（1）对活塞（或气缸）进行受力分析，画出受力示意图；

（2）列出活塞（或气缸）的平衡方程，求出未知量。

注意：

不要忘记气缸底部和活塞外面的大气压。

2.典例

例2如图5所示，一个横截面积为S的圆筒形容器竖直放置，金属圆板A的上表面是水平的，下表面是倾斜的，下表面与水平面的夹角为θ，圆板的质量为M。

不计圆板与容器内壁之间的摩擦。

若大气压强为P0，则被圆板封闭在容器中的气体压强P等于（）

A.B.

C.D.

1如图所示，活塞质量为m，缸套质量为M，通过弹簧吊在天花板上，气缸内封住了一定质量的空气，而活塞与缸套间无摩擦,活塞面积为S，则下列说法正确的是（）　（P0为大气压强）

■A、内外空气对缸套的总作用力方向向上，大小为Mg

■B、内外空气对缸套的总作用力方向向下，大小为mg

■C、气缸内空气压强为P0-Mg/S　

■D、气缸内空气压强为P0+mg/S

2、如图7，气缸由两个横截面不同的圆筒连接而成。

活塞A、B被轻刚性细杆连接在一起，可无摩擦移动。

A、B的质量分别为mA=12kg，mB=8.0kg，横截面积分别为SA=4.0×

10－2m2，SB=2.0×

10－2m2。

一定质量的理想气体被封闭在两活塞之间。

活塞外侧大气压强P0=1.0×

105Pa。

（1）气缸水平放置达到如图7所示的平衡状态，求气体的压强。

（2）现将气缸竖直放置，达到平衡后。

求此时气体的压强。

取重力加速度g=10m/s2。

二、图像类问题

一定质量的理想气体状态变化时，可以用图像表示气体状态的变化过程。

应用图像解题，形象、直观、思路清晰，既能达到化难为易的目的，又能训练学生灵活多变的思维能力。

1、利用图像判断气体状态变化过程,和能的转化和守恒定律判断气体做功、热传递及气体内能的变化

例1一定质量的理想气体，温度经过不同状态变化回到初始状态温度，可能的过程是：

A.先等压膨胀，后等容降压B.先等压压缩，后等容降压

C.先等容升压，后等压膨胀D.先等容降压，后等压膨胀

图3

例2一定质量的理想气体沿如图所示箭头方向发生状态变化，则下列说法正确的是：

A.ab过程放热，内能减少

B.bc过程吸收的热量多于做功值

C.ca过程内能一直不变

D.完成一个循环过程，气体放出热量

【练习】

1.一定质量的理想气体状态变化的p-T图像如图所示,由图像可知（）.

（A）气体在a、b、c三个状态的密度ρa＜ρc＜ρb

（B）在a→b的过程中,气体的内能增加

（C）在b→c的过程中,气体分子的平均动能增大

（D）在c→a的过程中,气体放热

2.一定质量的理想气体的状态变化过程如图中直线段AB所示，C是AB的中点，则（）.

（A）从状态A变化到状态B的过程中，气体的内能保持不变

（B）从状态A变化到状态B的过程巾，气体的温度先升高后降低

（C）从状态A变化到状态C，气体一定吸热

（D）从状态A变化到状态B的整个过程，气体一定吸热

2、图像与规律的转换,图像与图像之间的转换.

通过对物理图像的分析，根据图像提供的物理信息，我们可以将图像反映的物理过程“还原”成数学公式，而达到快捷、准确的解题目的。

理想气体状态变化的过程，可以用不同的图像描述，已知某个图像，可以根据这一图像转换成另一图像。

如由P-V图像变成P-T图像或V-T图像。

例3使一定质量的理想气体按图6中箭头所示的顺序变化，图中BC是一段以纵轴和横轴为渐近线的双曲线。

（1）已知气体在状态A的温度TA=300K，求气体在状态B、C和D的温度各是多少。

（2）将上述状态变化过程在V-T中用图线表示出来（图中要标明A、B、C、D四点，并且要画箭头表示变化的方向）。

说明每段图线各表示什么过程。

例4如图是一定质量的理想气体由状态A经过状态B变为状态C的V--T图象．已知气体在状态A时的压强是1.5×

105Pa.

（1）说出A到B过程中压强变化的情形，并根据图像提供的信息，计算图中TA的温度值．

01234T/×

100K

（2）请在图乙坐标系中，作出由状态A经过状态B变为状态C的P--T图像，并在图线相应位置上标出字母A、B、C．如果需要计算才能确定有关坐标值，请写出计算过程．

甲

【练习】

1、如图所示，水平放置的汽缸内壁光滑，活塞厚度不计，在A、B两处设有限制装置，使活塞只能在A、B之间运动，B左面汽缸的容积为V0，A、B之间的容积为0.1V0。

开始时活塞在B处，缸内气体的压强为0.9p0（p0为大气压强），温度为297K，现缓慢加热汽缸内气体，直至399.3K。

求：

（1）活塞刚离开B处时的温度TB；

（2）缸内气体最后的压强p；

（3）在右图中画出整个过程的p-V图线。

2.一定量的理想气体与两种实际气体I、II在标准大气压下做等压变化时的V－T关系如图（a）所示，图中＝。

用三份上述理想气体作为测温物质制成三个相同的温度计，然后将其中二个温度计中的理想气体分别换成上述实际气体I、II。

在标准大气压下，当环境温度为T0时，三个温度计的示数各不相同，如图（b）所示，温度计（ii）中的测温物质应为实际气体________（图中活塞质量忽略不计）；

若此时温度计（ii）和（iii）的示数分别为21︒C和24︒C，则此时温度计（i）的示数为________︒C；

可见用实际气体作为测温物质时，会产生误差。

为减小在T1－T2范围内的测量误差，现针对T0进行修正，制成如图（c）所示的复合气体温度计，图中无摩擦导热活塞将容器分成两部分，在温度为T1时分别装入适量气体I和II，则两种气体体积之比VI:

VII应为________。

三、综合计算问题

（一）变质量问题

1、恰当选取研究对象，将“变质量问题”转化为“定质量问题”

运用理想气体状态方程解决问题时，首先要选取一定质量的理想气体作为研究对象。

对于状态发生变化过程中，气体质量发生变化的问题，如充气，漏气等，如何选择适当的研究对象，将成为解题的关键。

例1　如右图所示，一容器有孔与外界相通，当温度由300K升高到400K时，容器中溢出的气体质量占原来的百分之几？

解法一：

解法二：

点评：

2、利用理想气体状态方程的推论，求解“变质量问题”

一定质量的理想气体（），若分成n个状态不同的部分，则。

在利用此推论求解“变质量问题”时，要注意初状态的气体质量与末状态的各部分气体质量之和相等。

例2　潜水艇的贮气筒与水箱相连。

当贮气筒中的空气压入水箱后，水箱便排出水，使潜水艇浮起。

某潜水艇贮气筒的容积是，贮有压强为的压缩空气。

一次，筒内一部分空气压入水箱后，压缩空气的压强变为，求贮气筒排出的压强为的压缩空气的体积。

（假设在整个过程中气体的温度未发生变化）

3、利用虚拟气体状态的方法求解“变质量问题”

例3　容积一定的容器中盛有压强为10大气压，温度为400K的某种理想气体，用去30克气体并把温度降为300K时，压强变为7大气压。

已知该气体在1大气压，300K时的密度为，求容器的容积和气体原来的质量。

（二）临界问题

1、气缸中的临界问题

h

例1：

如图所示，两个可导热的气缸竖直放置，它们的底部都由一细管连通（忽略细管的容积）。

两气缸各有一个活塞，质量分别为m1和m2，活塞与气缸无摩擦。

活塞的下方为理想气体，上方为真空。

当气体处于平衡状态时，两活塞位于同一高度h。

（已知m1＝3m，m2＝2m）

（1）在两活塞上同时放一质量为m0的物体，使m2恰好到达气缸底部。

求m0大小。

（2）在两活塞上同时各放一质量为m的物块，求气体再次达到平衡后两活塞的高度差（假定环境温度始终保持为T0）。

（3）在达到上一问的终态后，环境温度由T0缓慢上升到T，试问在这个过程中，气体对活塞做了多少功？

气体是吸收还是放出了热量？

（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）。

2、液柱中的临界问题

例2：

如图，一上端开口，下端封闭的细长玻璃管，下部有长l1=66cm的水银柱，中间封有长l2=6.6cm的空气柱，上部有长l3=44cm的水银柱，此时水银面恰好与管口平齐。

已知大气压强为p0=76cmHg。

如果使玻璃管绕底端在竖直平面内缓慢地转动一周，求在开口向下和转回到原来位置时管中空气柱的长度。

（封入的气体可视为理想气体，在转动过程中没有发生漏气。

）

练习：

如图所示，一开口气缸内盛有密度为的某种液体；

一长为的粗细均匀的小平底朝上漂浮在液体中，平衡时小瓶露出液面的部分和进入小瓶中液柱的长度均为。

现用活塞将气缸封闭（图中未画出），使活塞缓慢向下运动，各部分气体的温度均保持不变。

当小瓶的底部恰好与液面相平时，进入小瓶中的液柱长度为，求：

（1）此时气缸内气体的压强。

大气压强为，重力加速度为。

（2）若小瓶质量为m，用竖直向下的外力F向下压瓶底，当瓶底离液面高度为多少时，小瓶恰好浮不上来？

（三）液柱问题

1、“一团气”问题

例1：

上端开口、竖直放置的玻璃管，内横截面积为0.10cm2，管中有一段15cm长的水银柱将一些空气封闭在管中，如右图所示，此时气体的温度为27℃.当温度升高到30℃时，为了使气体体积不变，需要再注入多少克水银？

设大气压强为p0＝75cmHg且不变，水银密度ρ＝13.6g/cm3.

如图所示U形管左端开口、右端封闭，左管水银面到管口为18.6cm，右端封闭的空气柱长为10cm，外界大气压强Po＝75cmHg，在温度保持不变的情况下，由左管开口处慢慢地向管内灌入水银，试求再灌入管中的水银柱长度最多为多少厘米？

2、“两团气”问题

例1一根两端封闭，粗细均匀的玻璃管，内有一小段水银柱把管内空气柱分成a、b两部分，倾斜放置时，上、下两段空气柱长度之比La/Lb=2．当两部分气体的温度同时升高时，水银柱将如何移动？

如右图所示，均匀薄壁Ｕ形管，左管上端封闭，右管开口且足够长，管的横截面积为Ｓ，内装密度为ρ的液体．右管内有一质量为ｍ的活塞搁在固定卡口上，卡口与左管上端等高，活塞与管壁间无摩擦且不漏气．温度为Ｔ0时，左、右管内液面高度相等，两管内空气柱长度均为Ｌ，压强均为大气压强ｐ0．现使两边温度同时逐渐升高，求：

（1）温度升高到多少时，右管活塞开始离开卡口上升？

（2）温度升高到多少时，左管内液面下降ｈ？

（四）气缸问题

1、气缸与弹簧结合类问题

例1如图1（a）所示，长为2L的圆形气缸可沿水平面滑动，气缸与