届高三理科数学一轮复习学案 函数及其表示Word文件下载.docx

届高三理科数学一轮复习学案 函数及其表示Word文件下载.docx

《届高三理科数学一轮复习学案 函数及其表示Word文件下载.docx》由会员分享，可在线阅读，更多相关《届高三理科数学一轮复习学案 函数及其表示Word文件下载.docx（18页珍藏版）》请在冰豆网上搜索。

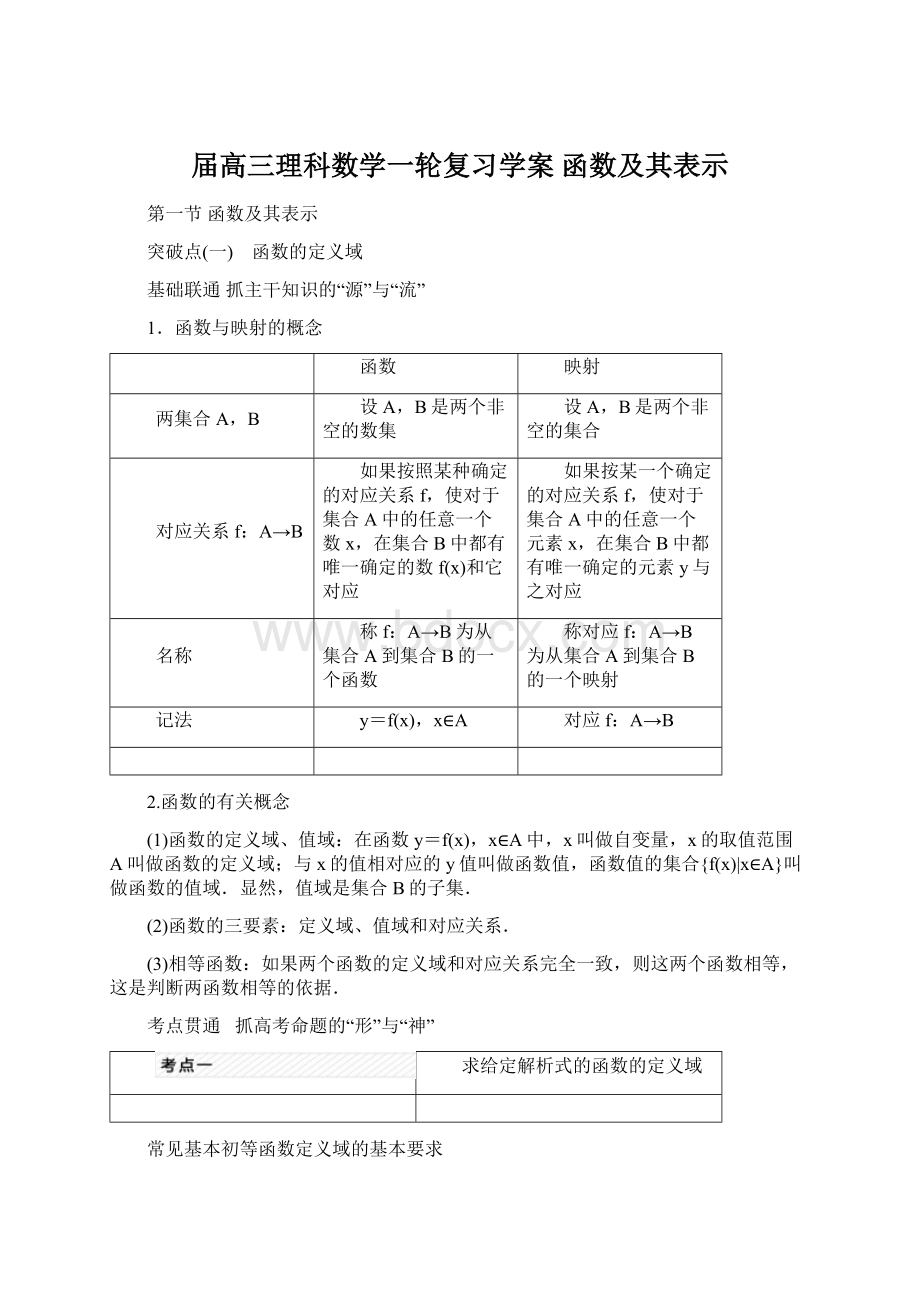
对应f：

2.函数的有关概念

（1）函数的定义域、值域：

在函数y＝f（x），x∈A中，x叫做自变量，x的取值范围A叫做函数的定义域；

与x的值相对应的y值叫做函数值，函数值的集合{f（x）|x∈A}叫做函数的值域．显然，值域是集合B的子集．

（2）函数的三要素：

定义域、值域和对应关系．

（3）相等函数：

如果两个函数的定义域和对应关系完全一致，则这两个函数相等，这是判断两函数相等的依据．

考点贯通抓高考命题的“形”与“神”

求给定解析式的函数的定义域

常见基本初等函数定义域的基本要求

（1）分式函数中分母不等于零．

（2）偶次根式函数的被开方式大于或等于0.

（3）一次函数、二次函数的定义域均为R.

（4）y＝x0的定义域是{x|x≠0}．

（5）y＝ax（a>

0且a≠1），y＝sinx，y＝cosx的定义域均为R.

（6）y＝logax（a>

0且a≠1）的定义域为（0，＋∞）．

（7）y＝tanx的定义域为.

[例1]　y＝－log2（4－x2）的定义域是（　　）

A．（－2,0）∪（1,2）B．（－2,0]∪（1,2）

C．（－2,0）∪[1,2）D．[－2,0]∪[1,2]

[解析]　要使函数有意义，必须

∴x∈（－2,0）∪[1,2）．

即函数的定义域是（－2,0）∪[1,2）．

[答案]　C

[易错提醒]

（1）不要对解析式进行化简变形，以免定义域发生变化．

（2）当一个函数由有限个基本初等函数的和、差、积、商的形式构成时，定义域一般是各个基本初等函数定义域的交集．

（3）定义域是一个集合，要用集合或区间表示，若用区间表示，不能用“或”连接，而应该用并集符号“∪”连接．

求抽象函数的定义域

对于抽象函数定义域的求解

（1）若已知函数f（x）的定义域为[a，b]，则复合函数f（g（x））的定义域由不等式a≤g（x）≤b求出；

（2）若已知函数f（g（x））的定义域为[a，b]，则f（x）的定义域为g（x）在x∈[a，b]上的值域．

[例2]　若函数y＝f（x）的定义域是[0,2]，则函数g（x）＝的定义域为________．

[解析]　由题意得，解得0≤x＜1，即g（x）的定义域是[0,1）．

[答案]　[0,1）

函数f[g（x）]的定义域指的是x的取值范围，而不是g（x）的取值范围．

已知函数定义域求参数

[例3]　（2017·

杭州模拟）若函数f（x）＝的定义域为一切实数，则实数m的取值范围是（　　）

A．[0,4）B．（0,4）

C．[4，＋∞）D．[0,4]

[解析]　由题意可得mx2＋mx＋1≥0恒成立．

当m＝0时，1≥0恒成立；

当m≠0时，则解得0<

m≤4.

综上可得：

0≤m≤4.

[答案]　D

[方法技巧]

已知函数定义域求参数的思想方法

已知函数的定义域，逆向求解函数中参数的取值，需运用分类讨论以及转化与化归的思想方法．转化与化归的思想方法是通过某种转化过程，将一个难以解决的问题转化为一个已经解决或者比较容易解决的问题，从而获解．

1．[考点一]函数y＝ln（2－x）的定义域为（　　）

A．（0,2）B．[0,2）

C．（0,1]D．[0,2]

解析：

选B　由题意知，x≥0且2－x>

0，解得0≤x＜2，故其定义域是[0,2）．

2．[考点一]（2017·

青岛模拟）函数y＝的定义域为（　　）

A．（－∞，1]B．[－1,1]

C．[1,2）∪（2，＋∞）D.∪

选D　由题意得

解得即－1≤x≤1且x≠－，

所以函数的定义域为∪.故选D.

3．[考点一]函数f（x）＝（a>

0且a≠1）的定义域为________．

由题意得解得即0<

x≤2，故所求函数的定义域为（0,2]．

答案：

（0,2]

4．[考点二]已知函数y＝f（x2－1）的定义域为[－，]，则函数y＝f（x）的定义域为________．

∵y＝f（x2－1）的定义域为[－，]，∴x∈[－，]，x2－1∈[－1,2]，∴y＝f（x）的定义域为[－1,2]．

[－1,2]

5．[考点三]若函数f（x）＝的定义域为{x|1≤x≤2}，则a＋b的值为________．

函数f（x）的定义域是不等式ax2＋abx＋b≥0的解集．不等式ax2＋abx＋b≥0的解集为{x|1≤x≤2}，所以解得所以a＋b＝－－3＝－.

－

突破点

（二）　函数的表示方法

能力练通抓应用体验的“得”与“失”

1．函数的表示方法

函数的表示方法有三种，分别为解析法、列表法和图象法．同一个函数可以用不同的方法表示．

2．应用三种方法表示函数的注意事项

（1）解析法：

一般情况下，必须注明函数的定义域；

（2）列表法：

选取的自变量要有代表性，应能反映定义域的特征；

（3）图象法：

注意定义域对图象的影响．与x轴垂直的直线与其最多有一个公共点．

3．函数的三种表示方法的优缺点

优点

缺点

解析法

简明扼要，规范准确

（1）有些函数关系很难或不能用解析式表示；

（2）求x与y的对应关系时需逐个计算，比较繁杂

列表法

能鲜明地显示自变量与函数值之间的数量关系

只能列出部分自变量及其对应的函数值，难以反映函数变化的全貌

图象法

形象直观，能清晰地呈现函数的增减变化、点的对称关系、最大（小）值等性质

作出的图象是近似的、局部的，且根据图象确定的函数值往往有误差

考点贯通抓高考命题的“形”与“神”

求函数的解析式

求函数解析式的四种方法

[典例]　

（1）如图，修建一条公路需要一段环湖弯曲路段与两条直道平滑连接（相切）．已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为（　　）

A．y＝x3－x2－x　　　

B．y＝x3＋x2－3x

C．y＝x3－x

D．y＝x3＋x2－2x

（2）定义在R上的函数f（x）满足f（x＋1）＝2f（x）．若当0≤x≤1时，f（x）＝x（1－x），则当－1≤x≤0时，f（x）＝________.

（3）（2017·

合肥模拟）已知f（x）的定义域为{x|x≠0}，满足3f（x）＋5f＝＋1，则函数f（x）的解析式为________．

[解析]　

（1）设该函数解析式为f（x）＝ax3＋bx2＋cx＋d，则f′（x）＝3ax2＋2bx＋c，

由题意知解得

∴f（x）＝x3－x2－x.

（2）∵－1≤x≤0，∴0≤x＋1≤1，

∴f（x）＝f（x＋1）＝（x＋1）[1－（x＋1）]＝－x（x＋1）．故当－1≤x≤0时，f（x）＝－x（x＋1）．

（3）用代替3f（x）＋5f＝＋1中的x，得3f＋5f（x）＝3x＋1，

∴

①×

3－②×

5得f（x）＝x－＋（x≠0）．

[答案]　

（1）A　

（2）－x（x＋1）　（3）f（x）＝x－＋（x≠0）

在求解析式时，一定要注意自变量的范围，也就是定义域．如已知f（）＝x＋1，求函数f（x）的解析式，通过换元的方法可得f（x）＝x2＋1，函数f（x）的定义域是[0，＋∞），而不是（－∞，＋∞）．

1.已知函数f（x）的定义域为（0，＋∞），且f（x）＝2f－1，则f（x）＝________.

在f（x）＝2f－1中，用代替x，得f＝2f（x）－1，将f＝2f（x）－1代入f（x）＝2f－1中，求得f（x）＝＋（x>

0）．

＋（x>

0）

2．函数f（x）满足2f（x）＋f（－x）＝2x，则f（x）＝________.

由题意知

解得f（x）＝2x.

2x

3．已知f（＋1）＝x＋2，求f（x）的解析式．

解：

设t＝＋1，则x＝（t－1）2，t≥1，代入原式有

f（t）＝（t－1）2＋2（t－1）＝t2－2t＋1＋2t－2＝t2－1.

故f（x）＝x2－1，x≥1.

4．已知f（x）是二次函数，且f（0）＝0，f（x＋1）＝f（x）＋x＋1，求f（x）的解析式．

设f（x）＝ax2＋bx＋c（a≠0），

由f（0）＝0，知c＝0，f（x）＝ax2＋bx，

又由f（x＋1）＝f（x）＋x＋1，

得a（x＋1）2＋b（x＋1）＝ax2＋bx＋x＋1，

即ax2＋（2a＋b）x＋a＋b＝ax2＋（b＋1）x＋1，

所以

解得a＝b＝.

所以f（x）＝x2＋x，x∈R.

5．已知f＝x2＋，求f（x）的解析式．

由于f＝x2＋＝2－2，

所以f（x）＝x2－2，x≥2或x≤－2，

故f（x）的解析式是f（x）＝x2－2，x≥2或x≤－2.

突破点（三）　分段函数

1．分段函数

若函数在其定义域内，对于定义域内的不同取值区间，有着不同的对应关系，这样的函数通常叫做分段函数．

2．分段函数的相关结论

（1）分段函数虽由几个部分组成，但它表示的是一个函数．

（2）分段函数的定义域等于各段函数的定义域的并集，值域等于各段函数的值域的并集．

分段函数求值

[例1]　

（1）设f（x）＝则f（f（－2））＝（　　）

A．－1B.

C.D.

（2）（2017·

张掖高三模拟）已知函数f（x）＝则f（1＋log25）的值为（　　）

A.B.

[解析]　

（1）因为f（－2）＝2－2＝，所以f（f（－2））＝f＝1－＝，故选C.

（2）因为2<

log25<

3，所以3<

1＋log25<

4，则4<

2＋log25<

5，则f（1＋log25）＝f（1＋log25＋1）＝f（2＋log25）＝＝×

＝×

＝，故选D.

[答案]　

（1）C　

（2）D

[方法技巧]

分段函数求值的解题思路

求分段函数的函数值，要先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，当出现f（f（a））的形式时，应从内到外依次求值．　

求参数或自变量的值或范围

[例2]　

（1）（2017·

西安模拟）已知函数f（x）＝若f（4）＝2f（a），则实数a的值为（　　）

A．－1或2B．2

C．－1D．－2

（2）设函数f（x）＝则使得f（x）≤2成立的x的取值范围是________．

[解析]　

（1）f（4）＝log24＝2，因而2f（a）＝2，即f（a）＝1，当a>

0时，f（a）＝log2a＝1，因而a＝2，当a≤0时，f（a）＝a2＝1，因而a＝－1，故选A.

（2）当x<

1时，由ex－1≤2得x≤1＋ln2，∴x<

1；

当x≥1时，由x≤2得x≤8，∴1≤x≤8.综上，符合题意的x的取值范围是x≤8.

[答案]　

（1）A　

（2）（－∞，8]

求分段函数自变量的值或范围的方法

求某条件下自变量的值或范围，先假设所求的值或范围在分段函数定义区间的各段上，然