年全国Ⅱ高考数学试题文Word文档格式.doc
《年全国Ⅱ高考数学试题文Word文档格式.doc》由会员分享,可在线阅读,更多相关《年全国Ⅱ高考数学试题文Word文档格式.doc(9页珍藏版)》请在冰豆网上搜索。
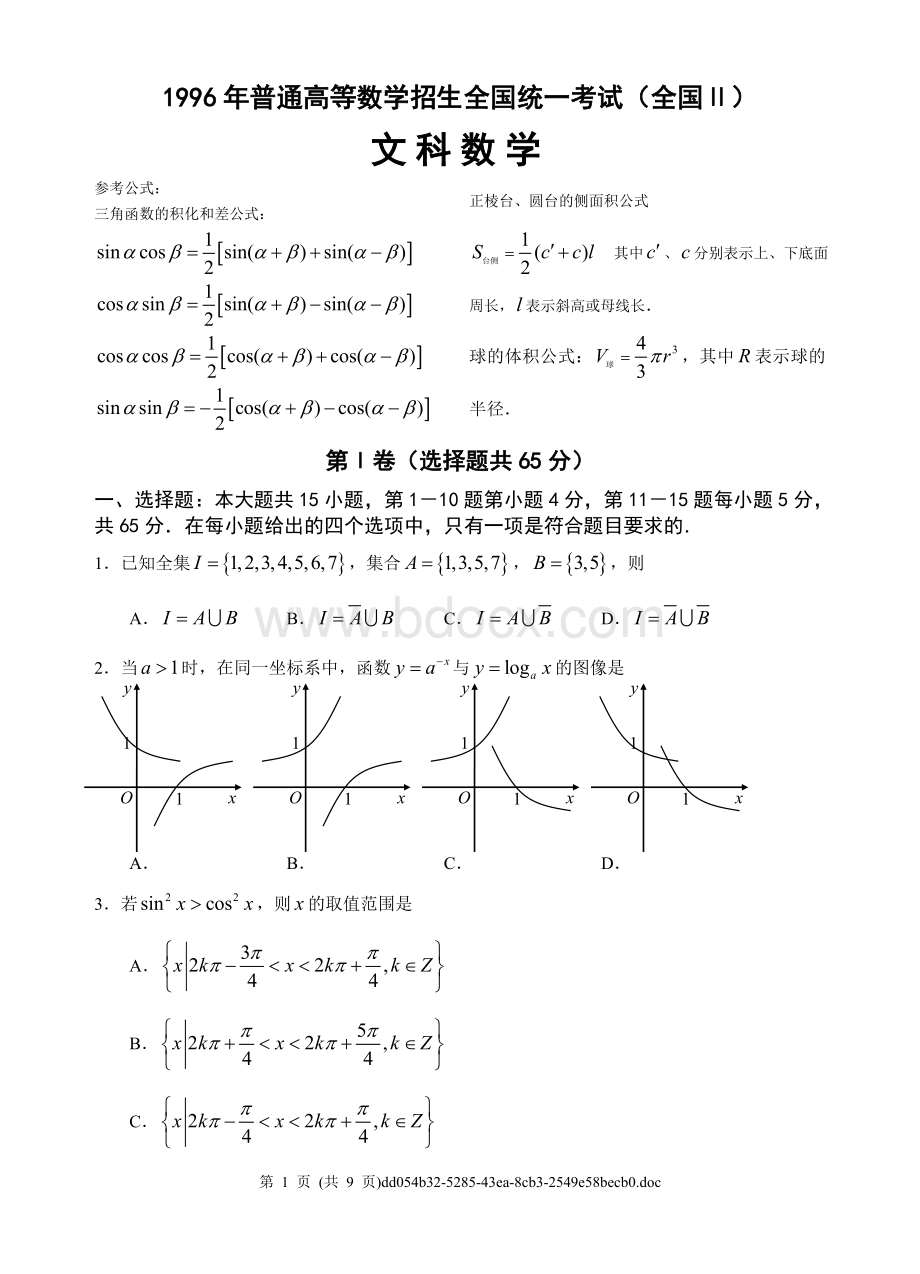
5.6名同学排成一排,其中甲、乙两必须排在一起的不同排法有
A.720种 B.360种C.240种 D.120种
6.已知是第三象限角,,则=
A. B.C. D.
7.如果直线与平面满足:
,∥,和,那么必有
A.且 B.且∥C.∥且 D.∥且
8.当时,函数的
A.最大值是1,最小值是-1 B.最大值是1,最小值是
C.最大值是2,最小值是-2 D.最大值是2,最小值是-1
8.若,则等于
9.中心在原点,准线方程为,离心率为的椭圆方程是
A. B. C. D.
10.圆锥母线长为1,侧面展开图圆心角为240°
,该圆锥的体积
11.椭圆的两个焦点坐标是
A., B.,
C., D.,
12.将边长为的正方形沿对角线折起,使得,则三棱锥的体积为
13.等差数列的前项和为30,前项和为100,则它的前项和为
A.130 B.170 C.210 D.260
14.设双曲线的半焦距为,直线过,两点,已知原点到直线的距离为,则双曲线的离心率为
A.2 B. C. D.
15.设是上的奇函数,,当时,,则等于
第Ⅱ卷(非选择题共85分)
注意事项:
用钢笔或圆珠笔直接答在答题卡上.
二、填空题:
本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
16.已知点与抛物线的焦点的距离是5,则=.
A
B
D
C
F
E
17.正六边形的中心和顶点共7个点,以其中3个点为顶点的三角形共有个(用数字作答).
18.的值是.
19.如图,正方形所在平面与正方形所在平面成60°
的二面角,则异面直线与所成角的余弦值是.
三、解答题:
本大题共6小题,共69分,解答应写出文字说明,证明过程或演算步骤.
20.(本小题满分11分)解不等式.
21.(本小题满分12分)设等比数列的前项和为.若,求数列的公比.
22.(本小题满分11分)已知△的三个内角、、满足:
,,求的值.
23.(本小题满分12分)
【注意:
本题的要求是,参照标①的写法,在标号②、③、④、⑤的横线上填写适当步骤,完成
(1)证明的全过程,并解答
(2).】
如图,在正三棱柱中,,,分别是,上的点,且,.
A1
B1
C1
(1)求证:
面面;
(2)求三棱锥的体积.
(1)证明:
在截面内,过作,是垂足.
①∵,,∥,延长与延长线交于,连结.
∴△∽△
∴
②
∴.
③
∴
④
⑤
∴面面.
24.(本小题满分12分)某地现有耕地10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?
(粮食单产=,人均粮食占有量=
25.(本小题满分12分)已知、是过点的两条互相垂直的直线,且、与双曲线各有两个交点,分别为、和、.
(1)求的斜率的取值范围;
(2)若恰是双曲线的一个顶点,求的值.
数学试题参考答案
一、选择题,本题考查基础知识,基本概念和基本运算能力
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题.本题考查基础知识,基本概念和基本运算技巧
13.
14.
15.
16.
三、解答题
17.
1996年普通高等学校招生全国统一考试数学试题(文史类)参考解答及评分标准
说明:
一.答指出了每题要考查主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准相应的评分细则.
二.对计算题,当考生的解答某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;
如果后继部分的解答较错误,就不再给分.
三.解答右端所注分数,表示考生正确做到这一步应得累加数.
四.只给整数分数,选择题和填空题不给中间分.
一.选择题:
本题考查基本知识和基本运算,第
(1)-(10)题每小题4分,第(11)-(15)题每小题5分.满分65分.
(1)C
(2)A(3)D(4)B(5)C
(6)D(7)A(8)D(9)A(10)C
(11)B(12)D(13)C(14)A(15)B
二.填空题:
本题考查基本知识和基本运算.每小题4分,满分16分.
(16)4(17)32(18)(19)
三.解答题
(20)本小题考查对数函数性质,对数不等式的解法,分类讨论的方法和运算能力,满分11分.
解:
(Ⅰ)当a>
1时,原不等式等价于不等式组:
解得x>
2a-1.
(Ⅱ)当0<
a<
解得a-1<
x<
2a-1
综上,当a>
1时,不等式的解集为{x|x>
2a-1};
当0<
1时,不等式的解集为{x|a-1<
2a-1}.
(21)本小题主要考查等比数列的基础知识,逻辑推理能力和运算能力.满分12分.
若q=1,则有S3=3a1,S6=6a1,S9=9a1.但a1≠0,即得S3+S6≠2S9,与题设矛盾,q≠1.
又依题意S3+S6=2S9可得整理得q3(2q6-q3-1)=0.
由q≠0得方程2q6-q3-1=0.(2q3+1)(q3-1)=0,
∵q≠1,q3-1≠0,∴2q3+1=0∴q=-
(22)本小题考查三角函数基础知识,利用三角公式进行恒等变形和运算能力.满分12分.
解法一:
由题设条件知B=60º
,A+C=120º
.
∵-=-2∴=-2
将上式化为cosA+cosC=-2cosAcosC
利用和差化积及积化和差公式,上式可化为
2coscos=-[cos(A+C)+cos(A-C)]
将cos=cos60º
=,cos(A+C)=代入上式得cos=-cos(A-C)
cos(A-C)=2cos2-1
代入上式并整理得4cos2+2cos-3=0,
(2cos-)(2cos+3)=0.
∵2cos+3≠0,∴2cos-=0,∴cos=.
解法二:
由题设条件知B=60º
.
设α=则=2α,可得A=60º
+α,C=60º
-α
所以=+
==
依题得,∵cosB=,∴.
整理得4cos2α+2cosα-3=0,(2cosα-)(2cosα+3)=0,
∵2cosα+3≠0,∴2cosα-=0从而得cos.
(23)本小题考查空间线面关系,正三棱柱的性质,逻辑思维能力,空间想象能力运算能力.满分12分.
(Ⅰ)②∵BE:
CF=1:
2∴DC=2BD,∴DB=BC,
③∵△ABD是等腰三角形,且∠ABD=120º
,∴∠BAD=30º
,∴∠CAD=90º
,
④∵FC⊥面ACD,∴CA是FA在面ACD上射影,且CA⊥AD,
⑤∵FA∩AC=A,DA⊥面ACF,DA面ADF
⑥∴面ADF⊥面ACF.
(Ⅱ)解:
∵.
在面A1B1C1内作B1G⊥A1C1,垂足为G.B1G=
面A1B1C1⊥面A1C∵B1G⊥面A1C,
∵E∈BB1,而BB1∥面A1C,∴三棱柱E-AA1F的高为
=AA1·
=∴
(24)本小题主要考查运用数学知识和方法解决实际问题的能力,指数函数和二项式定理的应用,近似计算的方法和能力.满分10分.
设耕地平均每年至多只能减少x公项,又设该地区现有人口为p人,粮食单产为M吨/公顷.
依题意得不等式
化简得x≤103×
[1-].
∵=103×
[1-×
(1+×
0.01+×
0.012+…)]
≈103×
1.1045]≈4.19分
∴x≤4(公顷)
答:
按规则该地区耕地平均每年至多只能减少4公顷.
(25)本小题主要考查直线与双曲线的性质,解析几何的基本思想,以及综合运用知识的能力.满分12分.
依题设:
l1、l2都存在,因为l1过点P且与双曲线有两个交点,故方程组
y=k1(x+)(k1≠0),
y2-x2=1①
有两个不同的解,在方程组①中消去y,整理得(-1)x2+2x+2-1=0②
若(-1)=0,则方程①只有一个解,则l1与以曲线只有一个交点,与题设矛盾.
故(-1)≠0,即|k1|≠1.方程②的判别式为
△1=
(2)2-4(-1)(2-1)=4(3-1)
设l2的斜率k2,因为l2过点P且与双曲线有两个交点,故方程组
y=k2(x+)(k2≠0),
y2-x2=1③
有两个不同的解,在方程组③中消去y,整理得(-1)x2+2x+2-1=0④
同理有(-1)≠0,△2=4(3-1)
又因为l1⊥l2,所以有k1·
k2=-1于是,l1、l2与双曲线各有两个交点,等价于
3-1>
0,
k1·
k2=-1,
|k1|≠1.
解得
,
|k1|≠1.
∴k1∈(-,-1)∪(-1,-)∪(,1)∪(1,)
(Ⅱ)双曲线y2-x2=1的顶点(0,1)、(0,-1).取A1(0,1)时,有
k1(0+)=1,解得k1=.从而k2==-.
将k2=-代入方程④得x2+4x+3=0⑤
记l2与