度《平行线》经典练习题含答案Word文档下载推荐.docx

度《平行线》经典练习题含答案Word文档下载推荐.docx

《度《平行线》经典练习题含答案Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《度《平行线》经典练习题含答案Word文档下载推荐.docx（16页珍藏版）》请在冰豆网上搜索。

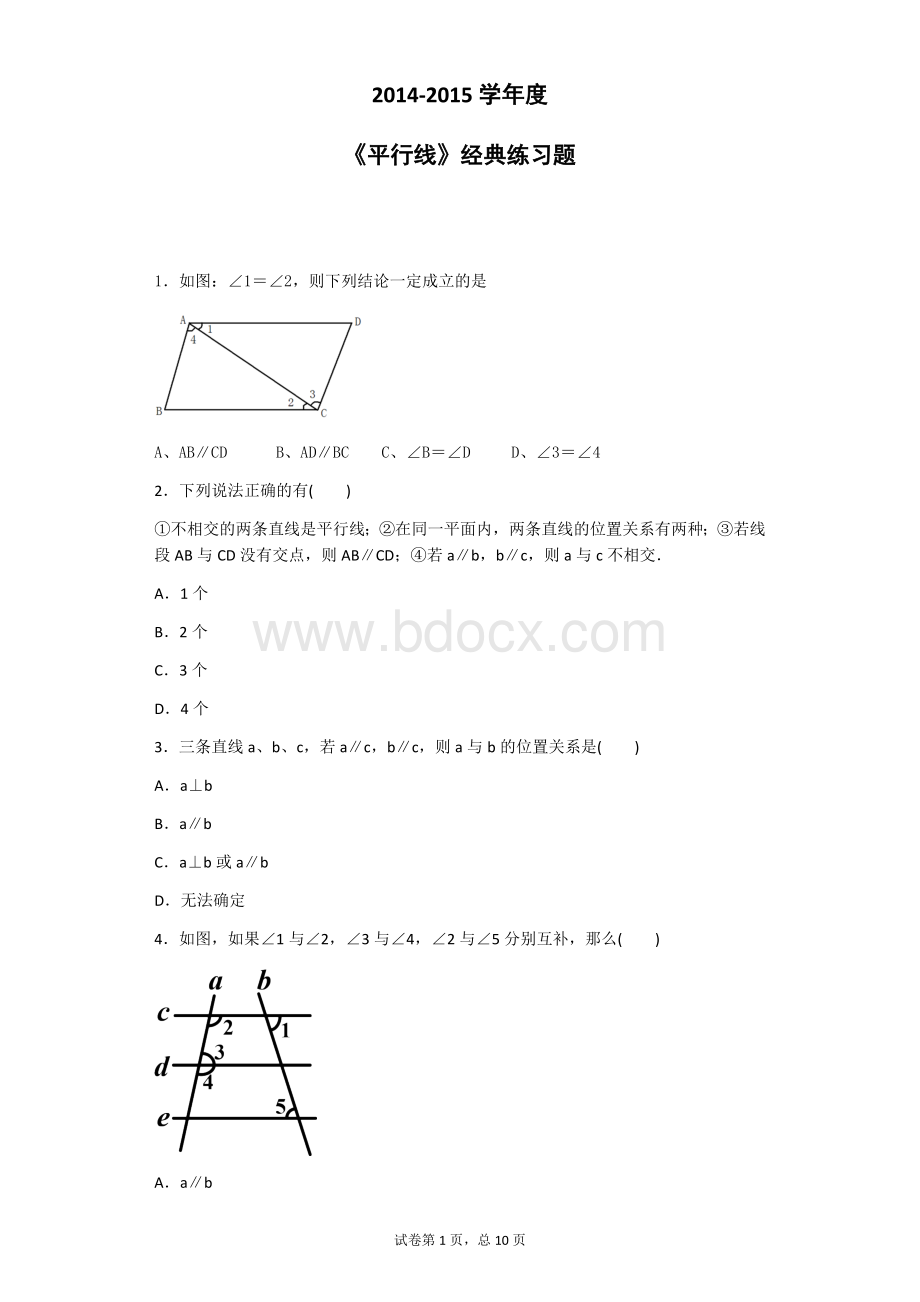
A．∠3＝∠4

B．∠1＝∠2

C．∠D＝∠DCE

D．∠D＋∠ACD＝180°

6．如图，是我们学过的用直尺和三角板画平行线的方法示意图，画图原理是（　　）

A．同位角相等，两直线平行

B．内错角相等，两直线平行

C．两直线平行，同位角相等

D．两直线平行，内错角相等

7．如图所示，∠1＝70°

，有下列结论：

①若∠2＝70°

，则AB∥CD；

②若∠5＝70°

③若∠3＝110°

④若∠4＝110°

，则AB∥CD．其中正确的有（　　）

8．在下面判断两条直线平行的方法中，正确的有（　　）

①在同一平面内，如果两条直线不相交，那么这两条直线重合或平行；

②平行于同一条直线的两条直线平行；

③在同一平面内，垂直于同一条直线的两条直线平行；

④同位角相等，两直线平行；

⑤内错角相等，两直线平行；

⑥同旁内角互补，两直线平行．

A．6个

B．5个

C．4个

D．3个

9．如图，下列说法中，正确的是（　　）

A．因为∠4＋∠D＝180°

，所以AD∥BC

B．因为∠C＋∠D＝180°

，所以AB∥CD

C．因为∠A＋∠D＝180°

D．因为∠A＋∠C＝180°

10．a、b、c是平面上任意三条直线，交点可以有（　　）

A．1个或2个或3个

B．0个或1个或2个或3个

C．1个或2个

D．都不对

11．下列说法正确的是（　　）

A．同一平面内没有公共点的两条线段平行

B．两条不相交的直线是平行线

C．同一平面内没有公共点的两条直线平行

D．同一平面没有公共点的两条射线平行

12．如图，用两个相同的三角板按照如图方式作平行线，能解释其中道理的定理是（）

A．同位角相等两直线平行

B．同旁内角互补，两直线平行

C．内错角相等两直线平行

D．平行于同一条直线的两直线平行

第II卷（非选择题）

请点击修改第II卷的文字说明

13．如图，直线a、b被直线c所截，若满足________，则a、b平行．

14．已知a，b，c为平面内三条不同直线，若a⊥b，c⊥b，则a与c的位置关系是________．

15．如图所示，若∠C＝60°

，∠AOF＝120°

，则________∥________．

16．找出下图中互相平行的线段（不考虑网格线上的线段）

17．如图，请完成下列各题．

（1）如果∠1＝________，那么DE∥AC；

（2）如果∠1＝________，那么EF∥BC；

（3）如果∠FED＋________＝180°

，那么AC∥ED；

（4）如果∠2＋________＝180°

，那么AB∥DF．

18．如图．

（1）如果∠1＝∠B，那么________∥________，根据是________________；

（2）如果∠3＝∠D，那么________∥________，根据是________________；

（3）如果要使BE∥DF，必须∠1＝________，根据是________________，

19．如图所示，能相交的是________，一定平行的是________．（填图形序号）

20．

（1）如图所示，b⊥a，c⊥a，请判断b与c的位置关系．

（2）用一句话总结

（1）中所包含的规律．

21．如图所示，光线从空气射入水中，再射出空气中，如果∠1＝∠2，∠3＝∠4，请你用所学的知识判断光线a、b是否平行，并说明理由．

22．如图所示，∠A＝∠ACE，∠B＝∠BDF，若要CE∥DF，∠A与∠B应满足怎样的条件？

试说明理由．

23．如图,已知:

AD是BC上的中线,且DF=DE．求证:

BE∥CF．（8分）

24．如图，在梯形ABCD中，AD∥BC，P是AB的中点，过P点作AD的平行线交DC于Q点．

（1）PQ与BC平行吗？

为什么？

（2）测量DQ与CQ的长，DQ与CQ是否相等？

（3）测量PQ、AD和BC的长度，你会发现PQ与AD＋BC有什么数量关系？

25．如图，已知A，B，C三点及直线EF，且AB∥EF，BC∥EF，那么A，B，C三点在同一条直线上吗？

26．（本题6分）已知：

如图，于D，点E为BC边上的任意一点，于F，且，求的度数。

27．（6分）完成下面的解题过程，并在括号内填上依据。

如图，EF∥AD,∠1=∠2,∠BAC=85°

.求∠AGD的度数

.

解：

∵EF∥AD,

∴∠2=____（）

又∵∠1=∠2

∴∠1=∠3

∴∥____（）

∴∠BAC+____=180°

∵∠BAC=85°

∴∠AGD=950

28．看图填空：

已知：

如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：

AD平分∠BAC．

证明：

∵AD⊥BC，EF⊥BC（已知）

∴∠ADC=90°

，∠EFC=90°

（垂线的定义）

∴=

∥

∴∠1=

∠2=

∵∠1=∠2（已知）

∴=

∴AD平分∠BAC（角平分线定义）

29．将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

（1）求证：

CF//AB

（2）求∠DFC的度数．

试卷第9页，总10页

。

参考答案

【答案】B

【解析】

试题分析：

】通过观察图形可知∠1和∠2是被直线AC所截形成的内错角，故根据内错角相等，两直线平行的判定方法可得到AD∥BC.

考点：

平行线的判定

点评：

此题考查的是平行线的判定方法，熟练通过分析图形确定角的关系是解题的关键.

2．B

【解析】①错，在同一平面内时①才成立；

②正确；

③错，两线段平行是指它们所在直线没交点；

④正确．故选B．

3．B

【解析】如果两条直线都与第三条直线平行，那么这两条直线也互相平行．

4．D

【解析】因为∠3和∠4是邻补角，是互补的，所以∠3和∠4互补这一条件无用．由∠1和∠2，∠2和∠5分别互补，可得到∠1＝∠5，所以c∥e，故选D．

5．B

【解析】∠1与∠2是直线AB，CD被BC所截构成的内错角，由两直线平行的条件可得AB∥CD，但不能判定BD∥AE，其余三个选项均可．

6．A

【解析】三角板的∠CAB，沿着FE进行平移后角的大小没变，而平移前后的两个角是同位角，所以画图原理是“同位角相等，两直线平行”．

7．B

【解析】②，④正确．②中∠5＝70°

，又∠2＝∠1＝70°

（对顶角相等），所以∠5＝∠2，所以AB∥CD（同位角相等，两直线平行）；

④中∠4＝110°

（对顶角相等），所以∠2＋∠4＝70°

＋110°

＝180°

，所以AB∥CD（同旁内角互补，两直线平行）．

8．A

【解析】平行线的判定方法包括6个：

一是平行线的定义；

二是在同一平面内平行于同一条直线的两条直线平行；

三是在同一平面内垂直于同一条直线的两条直线平行；

四是同位角相等，两直线平行；

五是内错角相等，两直线平行；

六是同旁内角互补，两直线平行．

9．C

【解析】∠A与∠D是AB和CD被AD所截得到的同旁内角，由同旁内角互补两直线平行，可得到AB∥CD；

∠C与∠D是AD与BC被DC所截得到的同旁内角，由同旁内角互补两直线平行，可得到AD∥BC；

易知D不正确．故C正确．

10．B

【解析】分情况讨论，一是三条直线平行；

二是只有两条直线平行；

三是三条直线都不平行．则交点可以为0个或1个或2个或3个．

11．C

【解析】判断平行时，前提条件必须是在同一平面内，另外，线段和射线的平行，是指它们所在的直线平行，故选C．

12．C.

由图可知，∠ABD=∠BAC，故使用的原理为内错角相等两直线平行．故选C．

平行线的判定．

13．∠1＝∠2（或∠2＝∠3或∠3＋∠4＝180°

）

【解析】答案不唯一，根据同位角相等两直线平行可得∠1＝∠2时，a∥b；

根据内错角相等两直线平行可得∠2＝∠3时，a∥b；

根据同旁内角互补两直线平行可得∠3＋∠4＝180°

时，a∥b．

14．平行

【解析】根据两条直线都垂直于同一直线，得到90°

角，根据平行线的三种判定方法，均可得出a与c平行的结论．

15．AB　CD

【解析】根据邻补角的性质得∠BOF＝180°

－∠AOF＝180°

－120°

＝60°

，所以∠C＝∠BOF，所以AB∥CD（同位角相等，两直线平行）．

16．AB∥GI，DE∥HJ，AC∥HF

【解析】根据平行线的定义解答

17．

（1）∠C　

（2）∠FED　（3）∠EFC　（4）∠1＋∠B

【解析】根据平行线的判定定理

18．

（1）AB；

CD；

同位角相等，两直线平行

（2）BE；

DF；

内错角相等，两直线平行

（3）∠D；

19．③；

⑤

【解析】借助图形的变化趋势发挥想象力．

20．b∥c，垂直于同一条直线的两条直线互相平行

（1）因为b⊥a，c⊥a（已知），所以∠1＝∠2＝90°

（垂直定义），所以b∥c（同位角相等，两直线平行）．

（2）规律：

垂直于同一条直线的两条直线互相平行．

21．平行．因为∠1＝∠2，∠3＝∠4（已知），所以∠1＋∠3＝∠2＋∠4，

所以a∥b（内错角相等，两直线平行）．

【解析】要判断光线a与b是否平行，找出截线是关键．由题图可知，光线在水中传播的路线所在的直线可作为截线，把实际问题抽象成数学问题，结合平行线的判定可知a∥b．

22．∠A＝∠B

【解析】理由：

因为∠A＝∠ACE，∠B＝∠BDF，当∠A＝∠B时，有∠ACE＝∠BDF．

又因为∠ACE＋∠ECD＝180°

，∠BDF＋∠FDC＝180°

，所以∠ECD＝∠FDC，所以EC∥DF．

23．证明：

∵AD是BC上的中线，

∴BD=DC．

又∵DF=DE（已知），

∠BDE=∠CDF（对顶角相等），

∴△BED≌△CFD（SAS）．

∴∠E=∠CFD（全等三角形的对应角相等）．

∴CF∥BE（内错角相等，两直线平行）．

欲证BE∥CF，需先证得∠EBC=∠FCD或∠E=∠CFD，那么关键是证△BED≌△CFD；

这两个三角形中，已知的条件